Исследование принципов кодирования и декодирования кодов Рида-Соломона на основе техники регистров сдвига, страница 5

Кодирующее устройство

Пусть порождающий многочлен (n,k)-кода имеет вид:

g(x)=g₀x⁰+g₁x¹+…+g_n-kx^n-k

В основе схем, реализующих кодирование по g(x), лежит схема деления на порождающий многочлен. Общий вид схемы кодера представлен на рис. 1:

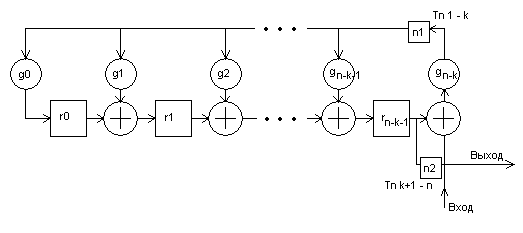рис. 1

Здесь r₀,r₁,…,r_n-k-1 – m-битовые регистровые ячейки, предназначенные для записи элементов поля GF(2³); g₀,g₁,…,g_n-k  - умножители, соответствующие коэффициентам g(x); n1,n2 – ключи (n1 замкнут с 1-го по k-ый такт, n2 – с (k+1)-го по n-ый такт).

         Алгоритм работы кодера:

1. На вход последовательно поступают информационные элементы, начиная со старшей степени. Благодаря тому, что вход подключен к регистру после последней (n-k)-ой регистровой ячейки достигается умножение кодируемой последовательности K(x) на x^n-k;

2. За k тактов работы схемы производится деление входной последовательности K(x)*x^n-k на g(x) и в регистровых ячейках формируются избыточные элементы;

3. С (k+1)-го по n-ый такт проверочные элементы последовательно выводятся из схемы. В результате на выходе кодера за n тактов работы схемы появляется комбинация кода Рида-Соломона f(x) с информационной частью K(x).

Декодирующее устройство

Для декодирования принятой последовательности будем использовать декодер вылавливания ошибок, схема которого для кода Рида-Соломона (7,3) изображена на рис. 2:

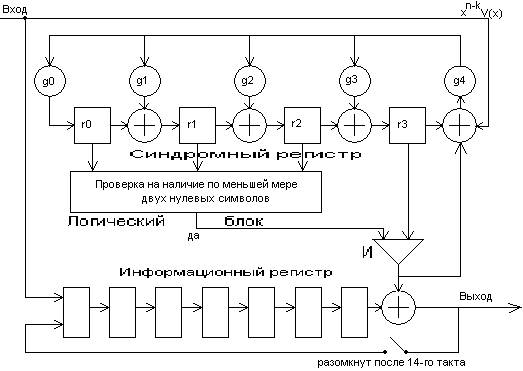рис. 2

         Автором метода вылавливания ошибок является Прейндж [1].

         У кода Рида-Соломона (7,3) d_min=5, следовательно, он исправляет однократные и двукратные ошибки.

         Декодер вылавливания ошибок исправляет ошибки последовательно за три 7-элементных цикла.

         Декодер состоит из двух регистров – синдромного и информационного, логического блока и схемы И.