


Задачи 2
Лекционный материал - лекции № 4 и № 5, 6.
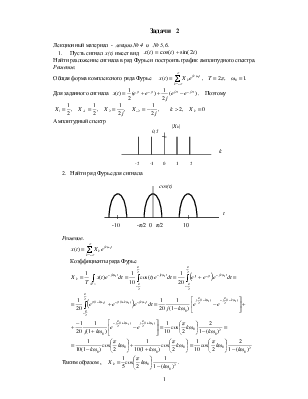
1.
Пусть сигнал x(t)
имеет вид ![]()
Найти разложение сигнала в ряд Фурье и построить график амплитудного спектра.
Решение.
Общая форма комплексного ряда Фурье 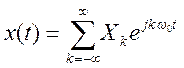 ,
, ![]()
Для заданного сигнала 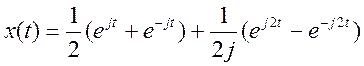 .
Поэтому
.
Поэтому
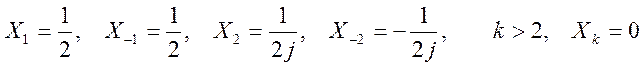
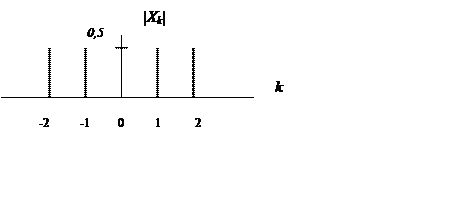 Амплитудный спектр
Амплитудный спектр
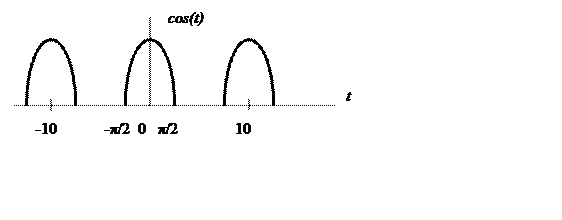
Решение.
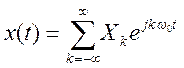
Коэффициенты ряда Фурье
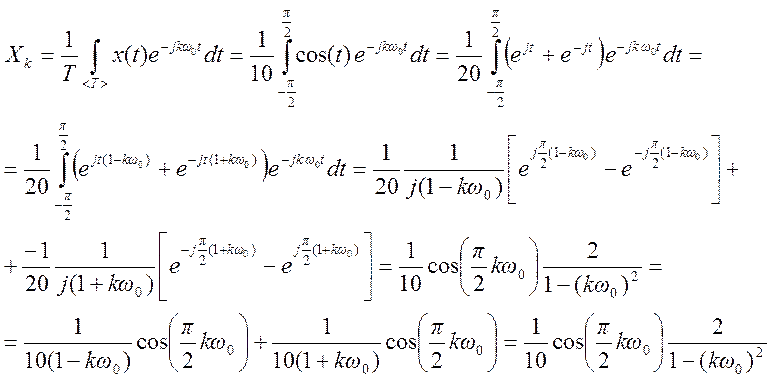
Таким образом , 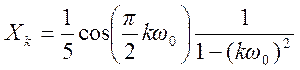 .
.
Для 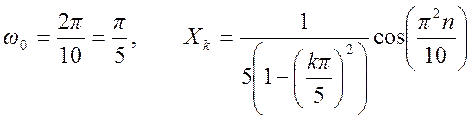 ,
, 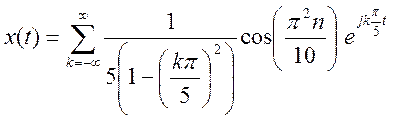
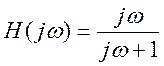 .
Найти постоянную составляющую выходного сигнала системы.
.
Найти постоянную составляющую выходного сигнала системы.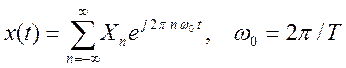 ,
,
выходной сигнал линейной системы имеет вид
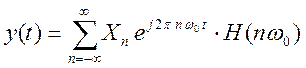 ,
,
где 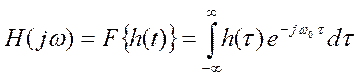 -
частотная характеристика системы.
-
частотная характеристика системы.
Для системы с частотной характеристикой 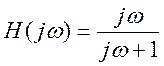
![]() ,
поэтому на выходе постоянная составляющая равна 0, т.е. система представляет
собой фильтр верхних частот , не пропускающий постоянную составляющую.
,
поэтому на выходе постоянная составляющая равна 0, т.е. система представляет
собой фильтр верхних частот , не пропускающий постоянную составляющую.
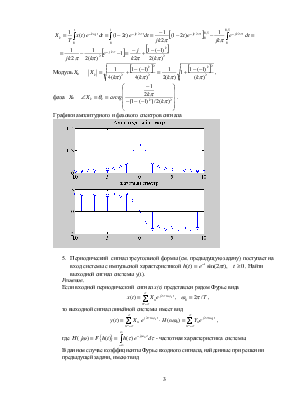
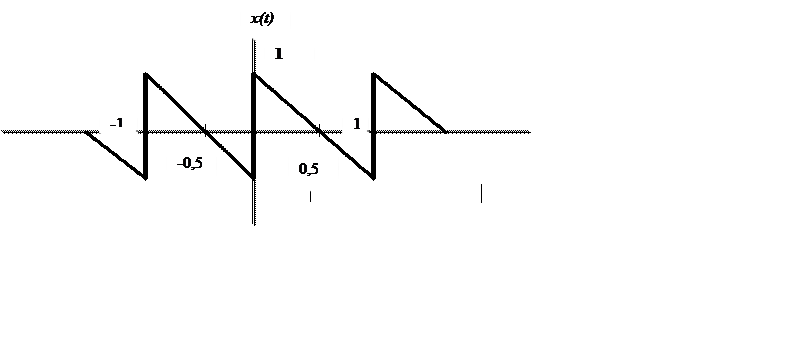
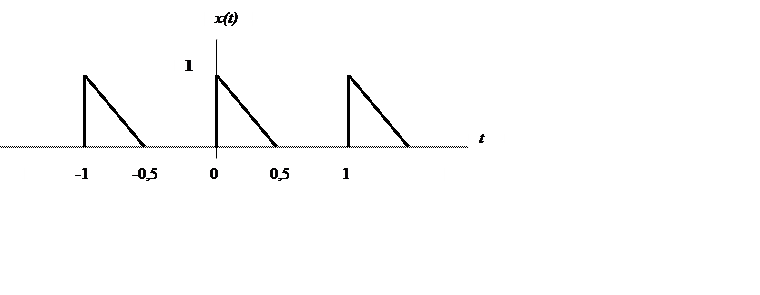 Найти и
построить амплитудный и фазовый спектры следующего сигнала
Найти и
построить амплитудный и фазовый спектры следующего сигнала Решение.
Аналитическое выражение сигнала 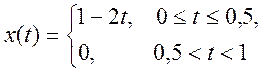
период сигнала равен 1, основная частота ![]() .
.
Коэффициенты комплексного ряда Фурье сигнала
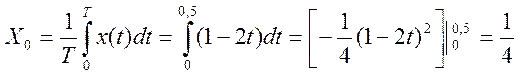 ,
,
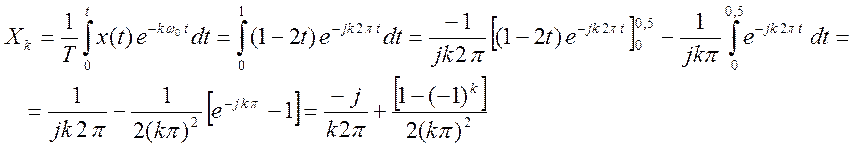
Модуль Xk 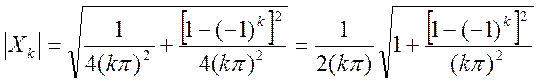 ,
,
фаза Xk 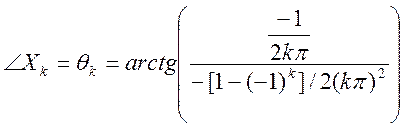 .
.
Графики амплитудного и фазового спектров сигнала
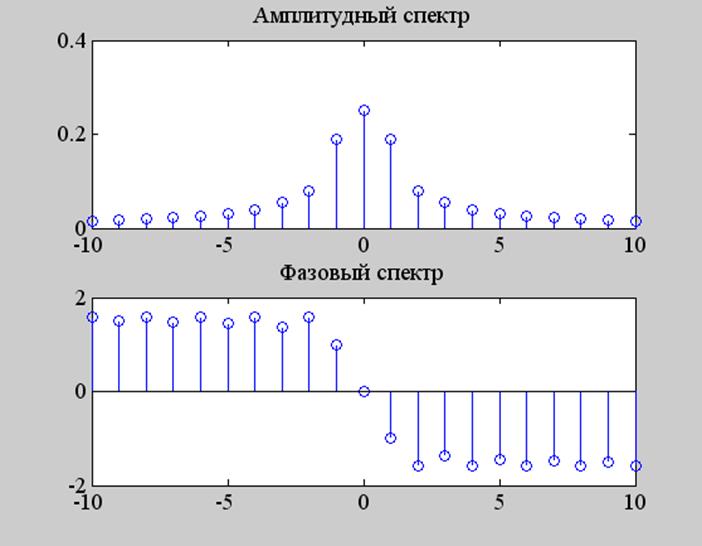
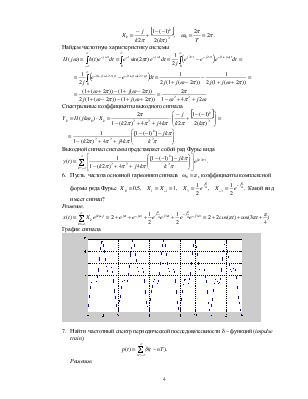
Решение.
Если входной периодический сигнал x(t) представлен рядом Фурье вида
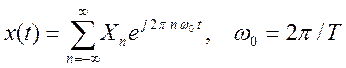 ,
,
то выходной сигнал линейной системы имеет вид
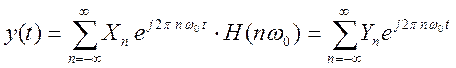 ,
,
где 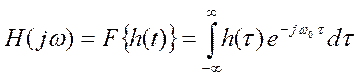 -
частотная характеристика системы.
-
частотная характеристика системы.
В данном случае коэффициенты Фурье входного сигнала, найденные при решении предыдущей задачи, имеют вид
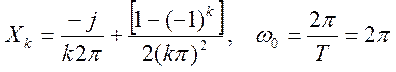 .
.
Найдем частотную характеристику системы
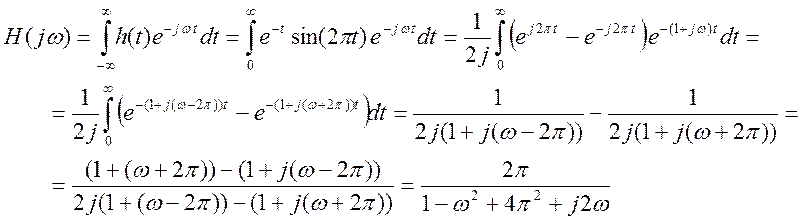
Спектральные коэффициенты выходного сигнала
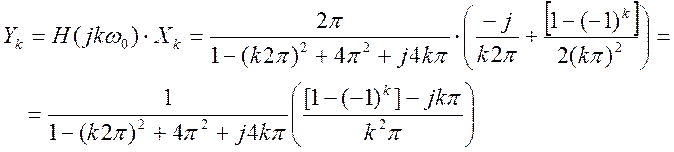
Выходной сигнал системы представляет собой ряд Фурье вида
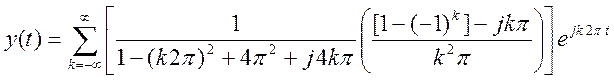 .
.
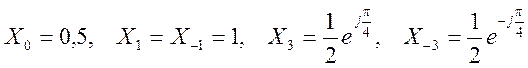 . Какой вид имеет
сигнал?
. Какой вид имеет
сигнал?Решение.
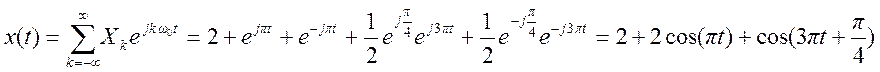
График сигнала
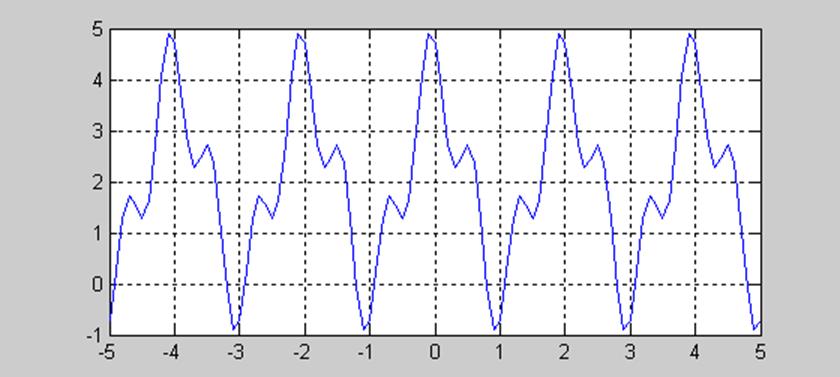
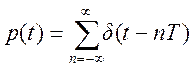 .
.
Решение.
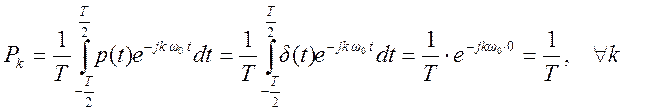
8. Сигнал y(t) образуется как полусумма периодического сигнала 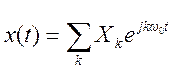 , сдвинутого влево и вправо на
значение t0, т.е.
, сдвинутого влево и вправо на
значение t0, т.е.
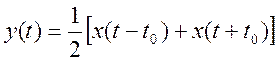 .
.
Найти ряд Фурье сигнала y(t) через ряд сигнала x(t). Определить значение t0, при котором в сигнале y(t) будет отсутствовать основная гармоника.
Решение.
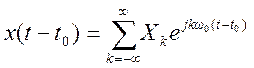 .
Поэтому
.
Поэтому
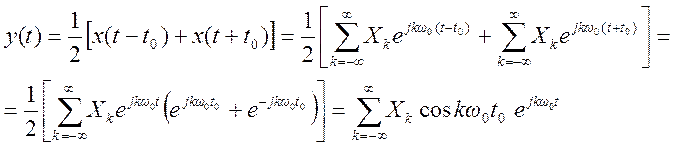
Первая гармоника будет
отсутствовать, если 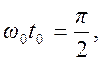 т.е.
т.е. 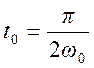
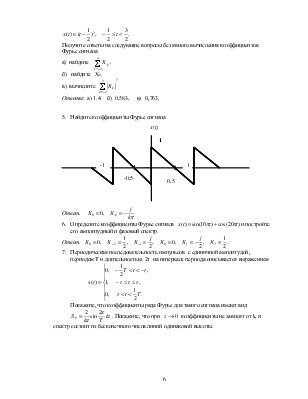
Задачи для самостоятельного решения.
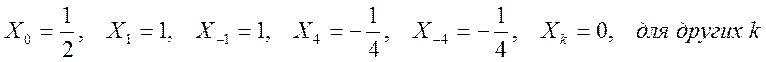 .
.

![]()




![]()
![]()
![]()

Ответ: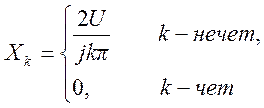
Ответ: ![]() .
.
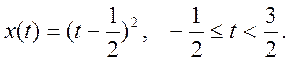
Получите ответы на следующие вопросы без явного вычисления коэффициентов Фурье сигнала
а) найдите  ,
,
б) найдите X0,
в) вычислите 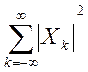
Ответы: а) 1.4. б) 0,583,
в) 0,763.
 |
Ответ. 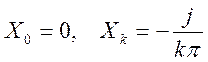
Ответ. 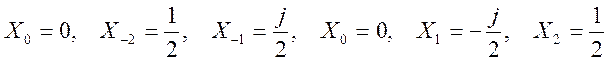 .
.
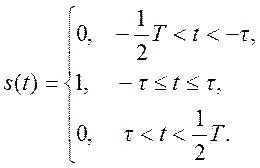
Покажите, что коэффициенты ряда Фурье для такого сигнала имеют вид
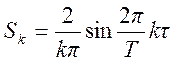 .
Покажите, что при
.
Покажите, что при ![]() коэффициенты не зависят
от k, и спектр состоит из бесконечного числа линий
одинаковой высоты.
коэффициенты не зависят
от k, и спектр состоит из бесконечного числа линий
одинаковой высоты.
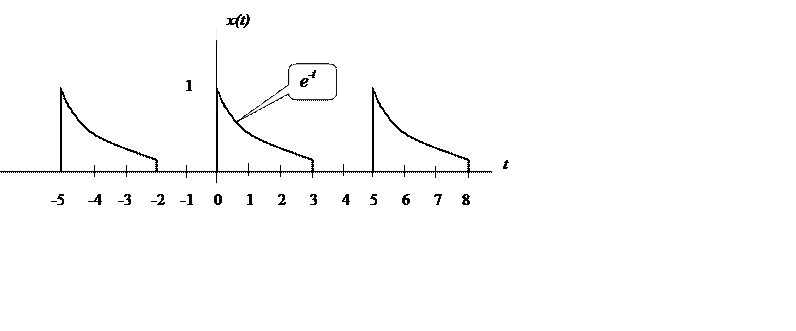 Определите
коэффициенты и ряд Фурье сигнала
Определите
коэффициенты и ряд Фурье сигналаОтвет. 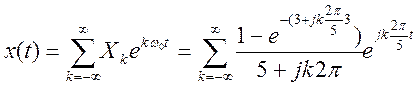
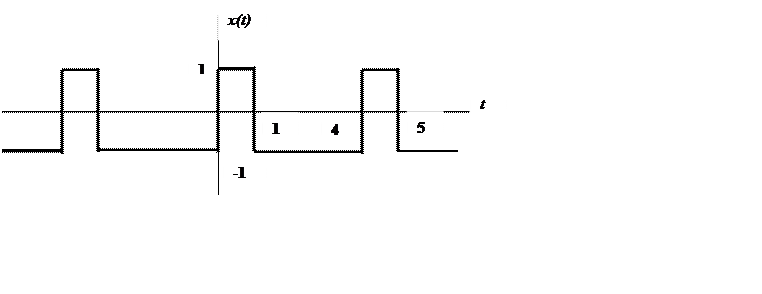 9.
Определите и постройте амплитудный и фазовый спектры периодического сигнала
9.
Определите и постройте амплитудный и фазовый спектры периодического сигнала
Ответ. 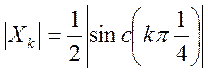 ,
, 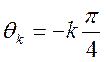
10. Разложите в ряд Фурье
сигнал
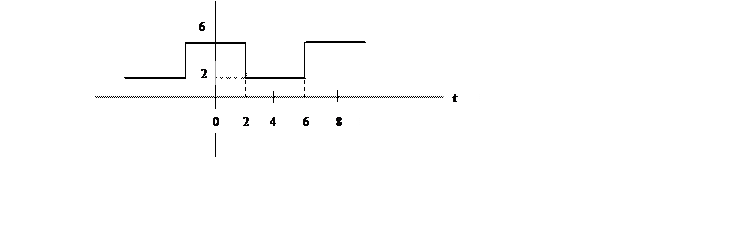
и постройте его амплитудный спектр.
Ответ. 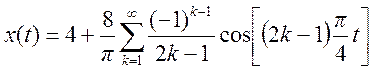
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.