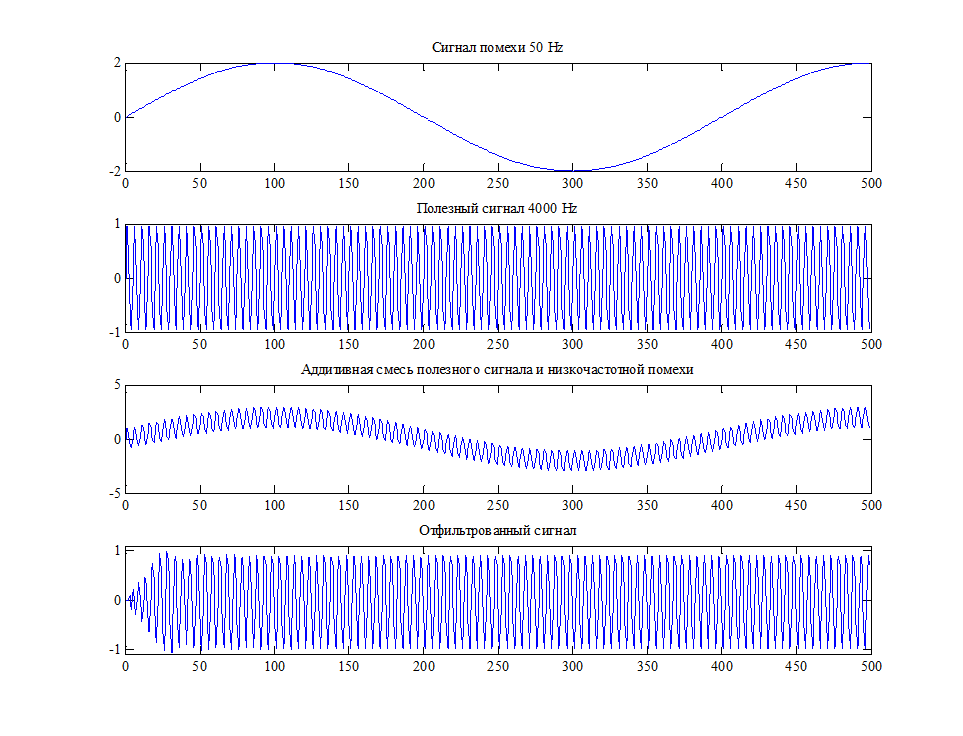
Информатика и выч. техника \ Теория и обработка сигналов

Проектирование цифрового БИХ-фильтра Чебышева 1-го типа верхних частот. Вариант 16, страница 3

Рис. 9. Сигнал помехи, полезный сигнал, их аддитивная смесь и сигнал на выходе фильтр.

Из графика видно, что фильтр хорошо пропускает высокочастотную полезную составляющую и подавляет низкочастотные помехи.


Фрагмент Matlab Script для иллюстрирования работы фильтра на граничных частотах:

N=1000;

i=0:1:N-1;

s1=sin(2*pi*2750*i/20000);

s2=sin(2*pi*3000*i/20000);

F1=filter(numd, dend, s1);

F2=filter(numd, dend, s2)

subplot(211);

plot(i, F1);

title('Реакция фильтра на сигнал с частотой 2750 Гц');

subplot(212);

plot(i, F2);

title('Реакция фильтра на сигнал с частотой 3000 Гц');

 

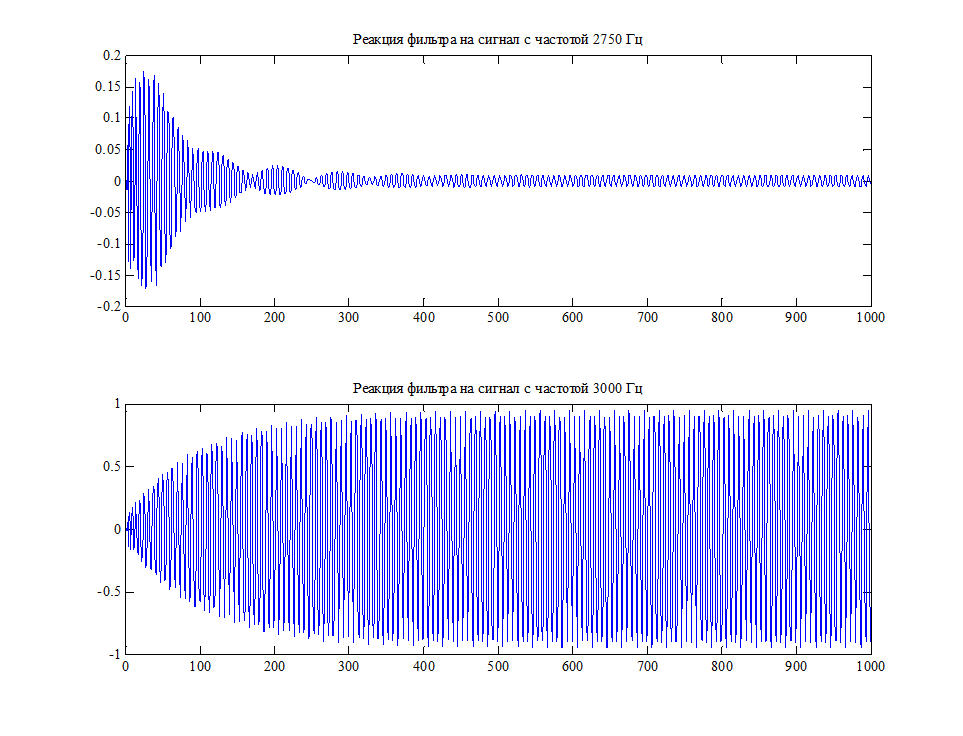
Рис.10. Фильтрация сигналов с граничными частотами.

График наглядно иллюстрирует, что фильтр на граничной частоте полосы задерживания – задерживает сигнал, а на граничной частоте пропускания – пропускает сигнал.


Программирование фильтра и оценка быстродействия.

Для оценки быстродействия полученного фильтра используется программа на языке C++, в качестве компилятора использовался Microsoft Visual C++ 6.0 (программа модифицирована под данный фильтр, основа программы – программа для оценки быстродействия фильтра студентки Худяковой Т.Н гр. АО-21).

//Листинг программы для оценки быстродействия

#include <stdio.h>

#include <iostream.h>

#include <math.h>

#include <windows.h>

#include <conio.h>

#define MAXS 100000                 // максимальная размерность массивов

//входного и выходного сигналов

#define N 20000                     // число отсчетов

int por=2;                           // порядок фильтров для каскадной формы

double b,B,a,A;                      // переменные для вычисления отсчетов

// выходного сигнала

double pi=3.141592653589;          

double Fd=20000;                   

double Td=1/Fd;                    

double y[MAXS];                     // массив для формирования отсчетов

// выходного сигнала

double x[MAXS];                     // массив для формирования отсчетов

//входного сигнала

double exit1[MAXS];                 // массивы передачи сигнала между элементами

double exit2[MAXS];                 // каскадной формы фильтра

double exit3[MAXS];

double exit4[MAXS];

double exit5[MAXS];                 // каскадной формы фильтра

double exit6[MAXS];

double exit7[MAXS];

double X1[3]={0.00173780201716, 0.00353414054081, -0.00174147401282};           

// коэффициенты полиномов числителя ПФ фильтра 2-го порядка

double Y1[3]={1,1.10768915931740 ,0.38282971367742};                        

//  коэффициенты полиномов знаменателя  ПФ фильтра 2-го порядка

double X2[3]={1,-2.33796856625263,1.37505253116290};            

double Y2[3]={1, 0.53005925145465,0.51793859935682};

double X3[3]={1, -2.20520122302418,1.23962425399669};

double Y3[3]={1, -0.11844312649894,0.67196892494537};

double X4[3]={1, -2.04427933438687,1.07558708082703};

double Y4[3]={1, -0.59154364917854,0.78886911535303};

double X5[3]={1, -1.70336367792585,0.72971206012283};           

double Y5[3]={1,  0.04692258458613,0.85937500000000};

double X6[3]={1, -1.77938551227314,0.80650626817012};

double Y6[3]={1, -1.07064940469863,0.92928004581301};

double X7[3]={1, -1.89611746554437,0.92484530450940};

double Y7[3]={1, -1.16456064244377,0.97730710590806};

double OS(double x[],int n, double m1[],double m2[])

// функция расчета выходного сигнала фильтра 2-го порядка

{                                                                     

for(int i=0;i<por+1;i++)

                  {

                        b=m1[i]*x[n-i];

                        B=b+B;

                  }

            for(i=1;i<por+1;i++)

                  {

                        a=m2[i]*y[n-i];

                        A=a+A;

                  }

            y[n]=B-A;

return y[n];

}    

DWORD WINAPI Thread_filter(LPVOID)                              

// отдельный поток для фильтрации сигнала

{

double OS(double x[],int n,double m1[],double m2[]);

// определение функции расчета выходного сигнала  с фильтра 2-го порядка

double s,s_1;                      

//определение переменных для подсчета временного интервала фильтрации

s = GetTickCount();                

// получение значения счетчика времени

for(int n=0;n<N;n++)          // фильтрация входного сигнала

      {

            exit1[n]=OS(x,n,X1,Y1);

            exit2[n]=OS(exit1,n,X2,Y2);

            exit3[n]=OS(exit2,n,X3,Y3);

            exit4[n]=OS(exit3,n,X4,Y4);

            exit5[n]=OS(exit4,n,X5,Y5);

            exit6[n]=OS(exit5,n,X6,Y6);

            exit7[n]=OS(exit6,n,X7,Y7);

        }

      s_1 = GetTickCount() - s;    

// вычисление времени фильтрации входного сигнала в миллисекундах

      cout<<endl;

      cout<<"N="<<N;

      cout<<endl;

      cout<<"General time to filtering : ";

      cout<<s_1<<" ms"<<endl;

      cout<<"Time to filtering ones sample: ";

      cout<<(s_1*1000)/N<<"mcs"<<endl;

      return 0;  

}

void main()

{

unsigned long ThreadId;       // определение идентификатора потока

      for(int j=0;j<N;j++)

      {

      x[j]=2*cos(2*pi*12100*Td*j)+cos(2*pi*9800*Td*j);

// расчет гармонического входного сигнала

      }

CreateThread(NULL,0,Thread_filter,x,0,&ThreadId);   

// создание и запуск потока для начала фильтрации сигнала

getch();

}

Программа выполнялась на персональном компьютере, на базе процессора IntelCeleronD 331 с тактовой частотой 2,66 Гц, 512 Mb RAM.

Таблица 1. Результаты работы программы для определения быстродействия фильтра

N

t

T

2000

62 мс

31 мкс

5000

172 мс

34.4 мкс

10000

344 мс

34.4 мкс

20000

703 мс

35.15 мкс

50000

1750 мс

35 мкс

Среднее время обработки одного отсчета составляет 33,99 мкс.


Заключение.

В ходе данной курсовой работы был спроектирован цифровой БИХ-фильтр верхних частот Чебышева 1 рода (пульсация в зоне проводимости), удовлетворяющий заданной спецификации. Фильтр был рассчитан методом билинейного преобразования, относящегося к методам, основанным на аналоговых прототипах, из-за простоты проектирования и высокого качества результирующего фильтра. Получившийся  фильтр имеет довольно хорошую амплитудно-частотную характеристику, но его фазо-частотная характеристика нелинейная.

Была предложена каскадная (последовательная) форма реализации фильтра, выполненная на 7 фильтрах второго порядка. АЧХ полученной системы полностью удовлетворяет спецификации.

 Также было проведено тестирование фильтра, где фильтр показал себя с лучшей стороны. Тестирование заключалось в пропускании через фильтр аддитивной смеси двух сигналов: высокочастотного (полезного) и низкочастотного (помехи). На выходе наблюдалась только высокочастотная составляющая, что свидетельствует о хорошей работе фильтра.

В последнем пункте курсовой работы была произведена оценка быстродействия фильтра.


Список литературы.

  1. Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов: Учеб. пособие. – Новосибирск: Изд-во НГТУ, 1998. – Ч.2. – 115  с.
  2. Курс лекций по дисциплине «Теория и обработка сигналов», преподаватель доц. Щетинин Ю.И. Учебный год: 2005-2006 (лекции 24-28)

Скачать файл