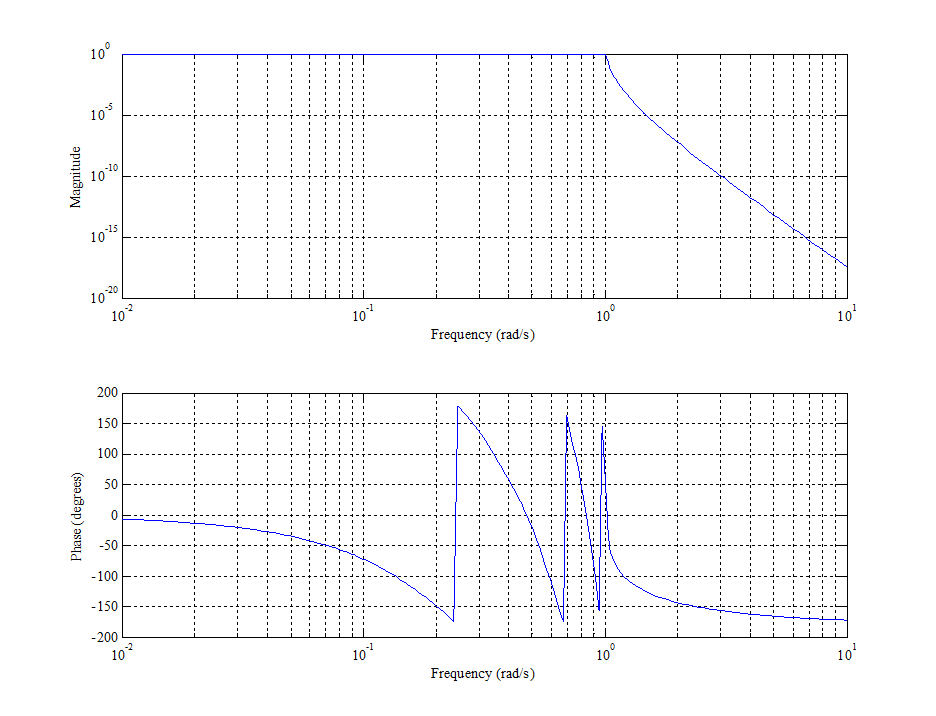
Информатика и выч. техника \ Теория и обработка сигналов

Проектирование цифрового БИХ-фильтра Чебышева 1-го типа верхних частот. Вариант 16, страница 2

 

Рис. 2. АЧХ и ФЧХ НФНЧ.

Преобразование НФНЧ в аналоговый ФВЧ с помощью частотного преобразования :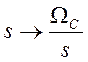

[bt , at] = LP2HP (b, a, Wo) – функция Matlab для трансформации коэффициентов передаточной функции  фильтра нижних частот в фильтр верхних частот.

[bt, at] = lp2hp (b, a, 0.50952544949443)

bt =

bt0-bt4

bt5-bt9

bt10-bt4

0.94406087628592

-0.00000000000001

0.00000000000000

0.00000000000000

0.00000000000001

-0.00000000000000

0.00000000000004

0.00000000000000

0.00000000000000

-0.00000000000000

-0.00000000000000

-0.00000000000000

-0.00000000000001

-0.00000000000000

0.00000000000000

at = 1.0e+002 *

at0-at4

at5-at9

at10-at14

0.01000000000000

0.87009439183045

0.21353201848537  

0.06161556432509 

1.03371778157729 

0.06223530602182

0.21749224444735 

0.74687205770683  

0.03427737062441  

0.43370906990201  

0.65663663696077  

0.00478298839802  

0.77408403589043 

0.31130267394347 

0.00214745975803

Преобразование аналогового ФВЧ в цифровой ФВЧ с помощью билинейного преобразования:

[NUMd, DENd] = BILINEAR (NUM, DEN, Fs) – функция Matlab для билинейного преобразования коэффициентов передаточной функции АФ в коэффициенты передаточной функции ЦФ.

[numd, dend] = bilinear(bt, at, 0.5)

numd =

numd0-numd4

numd5-numd9

numd10-numd14

0.00173780201716 

-3.47907963834764

1.73953981917384 

-0.02432922824019  

5.21861945752144 

-0.63255993424504

0.15813998356125

-5.96413652288168  

0.15813998356126

-0.63255993424503  

5.21861945752149 

-0.02432922824020  

1.73953981917381 

-3.47907963834767  

0.00173780201716

dend =

dend0-dend4

dend5-dend9

dend10-dend14

1.00000000000000 

-3.82095693715313

0.56190235937284  

-2.19944914294659  

3.60046568328836 

   0.06535454240270

4.97217243772519 

-0.71011342362416  

0.30845999595192 

-5.37143140826946  

1.24102442645085  

-0.03140558014400  

6.55080659990994 

0.22667394231546  

0.08306958653557

Расположение нулей и полюсов передаточной функции ЦФ:

zplane (numd ,dend) – построение диаграммы нулей и полюсов.

Рис. 3. Диаграмма нулей и полюсов.

По условию устойчивости полюсы должны быть внутри единичного круга на плоскости z. Из полученной диаграммы видно, что спроектированный фильтр устойчив, так как все его полюса строго лежат внутри круга единичного радиуса.

Частотные характеристики ЦФ:

Фрагмент кода для построения графиков АЧХ и ФЧХ ЦФ:

[k,f]= freqz(numd, dend, 512, 20000);

subplot(211)

plot(f, abs(k))

xlabel('Frequency, Hz ')

subplot(212)

plot(f, 20*log10(abs(k)))

xlabel('Frequency, Hz ')

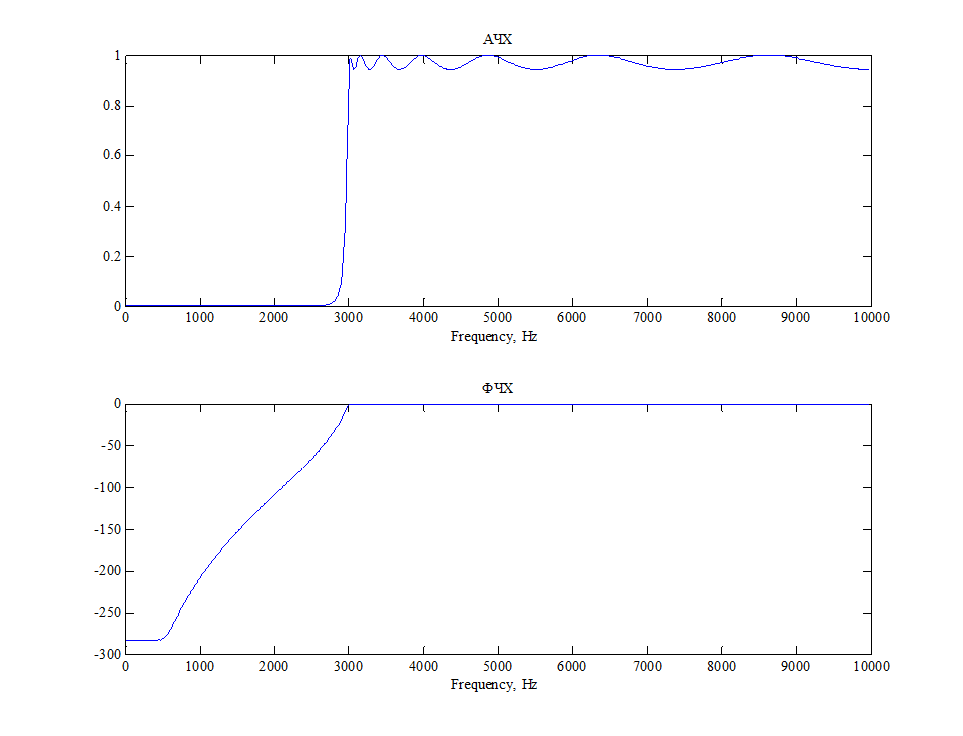
Рис.4. АЧХ и ФЧХ ЦФ.

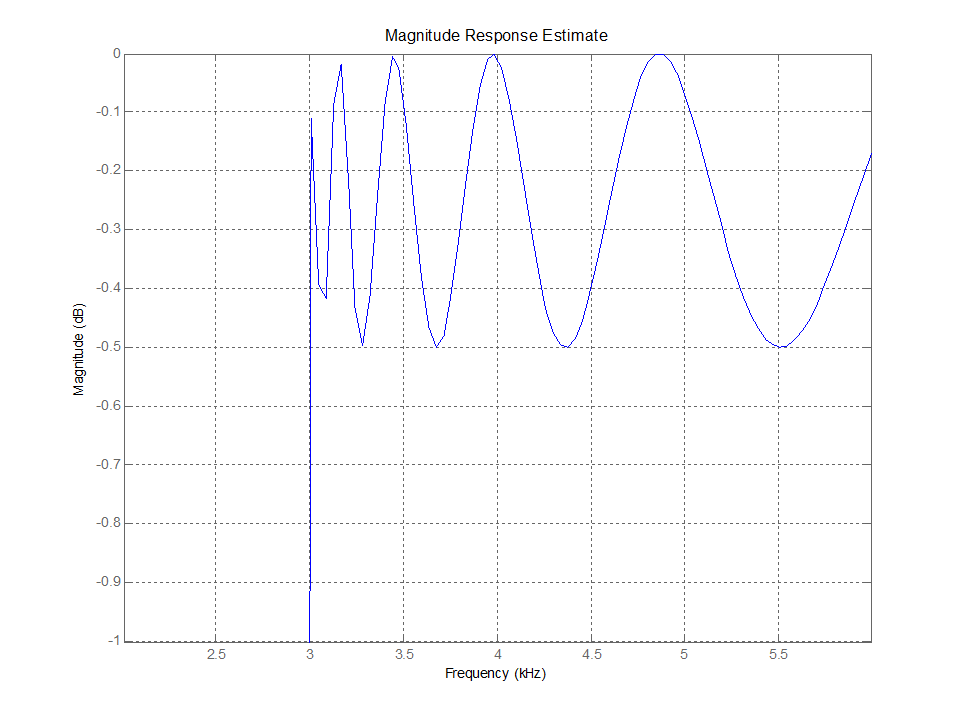
Рис. 5. Пульсация в полосе пропускания (увеличенный масштаб)

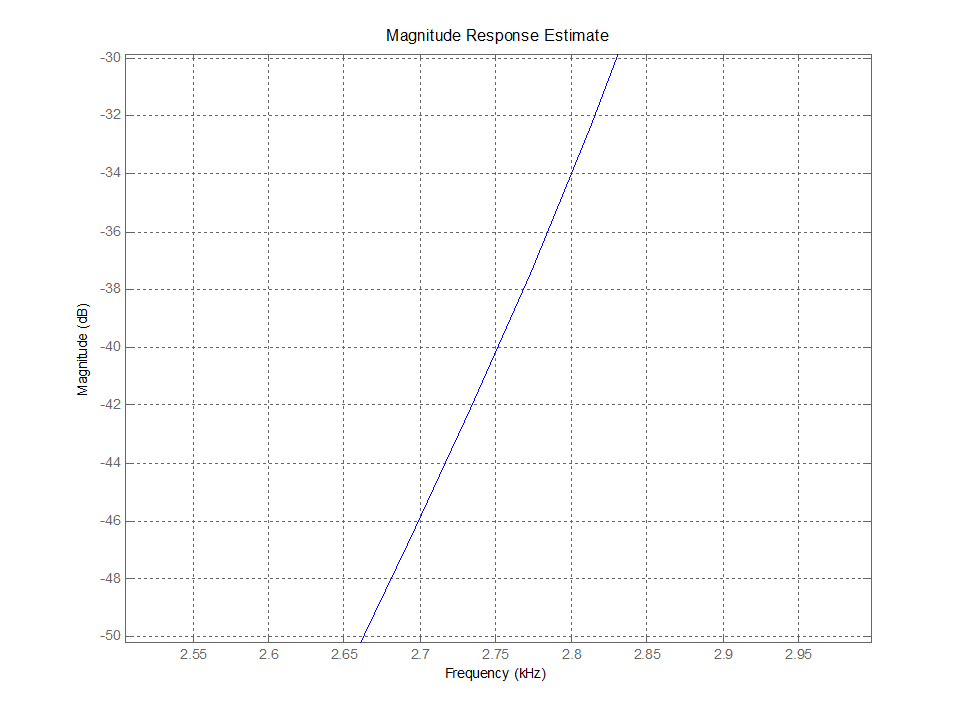
Рис. 6. Граничная частота задерживания (увеличенный масштаб)

Данные графики наглядно показывают, что АЧХ фильтра полностью соответствует его спецификации.


Уравнение фильтра.

Передаточная функция ФВЧ  имеет вид дробно-рационального выражения:

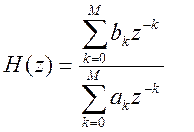
В общем виде линейный цифровой фильтр описывается линейным разностным уравнением с постоянными коэффициентами:

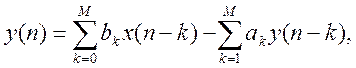
где x(n) – входной сигнал, y(n) – выходной сигнал, ak, bk – коэффициенты фильтра.

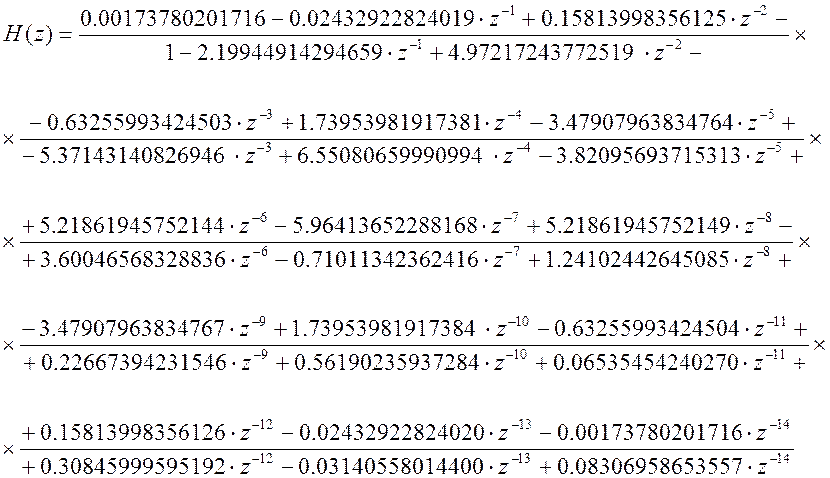
Следовательно, уравнение фильтра будет иметь следующий вид:

y(n)= 0.00173780201716x(n)-0.02432922824019x(n-1)+ 0.15813998356125x(n-2)-

-0.63255993424503x(n-3)+1.73953981917381x(n-4)-3.47907963834764x(n-5)+ +5.21861945752144x(n-6)-5.96413652288168x(n-7)+5.21861945752149x(n-8)-

-3.47907963834767x(n-9)+1.73953981917384x(n-10)-0.63255993424504x(n-11)+

+0.15813998356126x(n-12)-0.02432922824020x(n-13)+0.00173780201716x(n-14)+

+2.19944914294659y(n-1)-4.97217243772519y(n-2)+5.37143140826946y(n-3)-

-6.55080659990994y(n-4)+3.82095693715313y(n-5)-3.60046568328836y(n-6)+

+0.71011342362416y(n-7)-1.24102442645085y(n-8)-0.22667394231546y(n-9)-

-0.56190235937284y(n-10)-0.06535454240270y(n-11)-0.30845999595192y(n-12)+

+0.03140558014400y(n-13)-0.08306958653557y(n-14)


Реализация фильтра.

Для реализации рассчитанного  фильтра я использую  последовательную (каскадную) форму реализации, так как она менее чувствительна к погрешностям квантования. Для этого были использованы следующие функции MatLab:

[z,p,k]=tf2zp(numd, dend)

sos=zp2sos(z,p,k)

sos =

0.00173780201716 

0.00353414054081  

-0.00174147401282  

1.00000000000000 

1.10768915931740

0.38282971367742

1.00000000000000 

-2.33796856625263  

1.37505253116290  

1.00000000000000  

0.53005925145465  

0.51793859935682

1.00000000000000 

-2.20520122302418

1.23962425399669  

1.00000000000000 

-0.11844312649894  

0.67196892494537

1.00000000000000 

-2.04427933438687  

1.07558708082703  

1.00000000000000 

-0.59154364917854  

0.78886911535303

1.00000000000000 

-1.70336367792585  

0.72971206012283  

1.00000000000000 

-0.89200073089876  

0.87021451069460

1.00000000000000 

-1.77938551227314  

0.80650626817012  

1.00000000000000 

-1.07064940469863  

0.92928004581301

1.00000000000000

-1.89611746554437  

0.92484530450940  

1.00000000000000

-1.16456064244377  

0.97730710590806

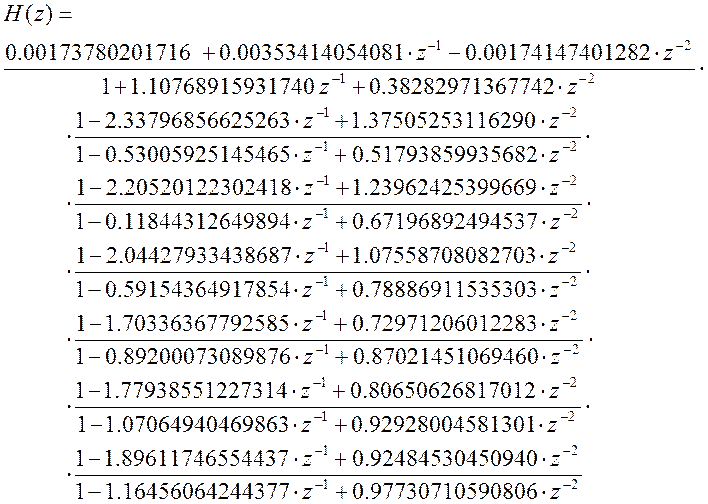
Рис. 7. Структурная схема каскадной реализации фильтра.

Фрагмент кода Matlab Script для построения графиков АЧХ исходного фильтра и фильтра в каскадной форме:

[z, p, k]=sos2zp(sos);

[b_q, a_q]=zp2tf(z, p, k);

[H_q, f1]=freqz(b_q, a_q, 256, 20000);

figure(3)

plot(f, abs(H), f1,abs(H_q), '--');

grid;

legend('АЧХ ЦФ', 'АЧХ ЦФ в каскадной форме представления')

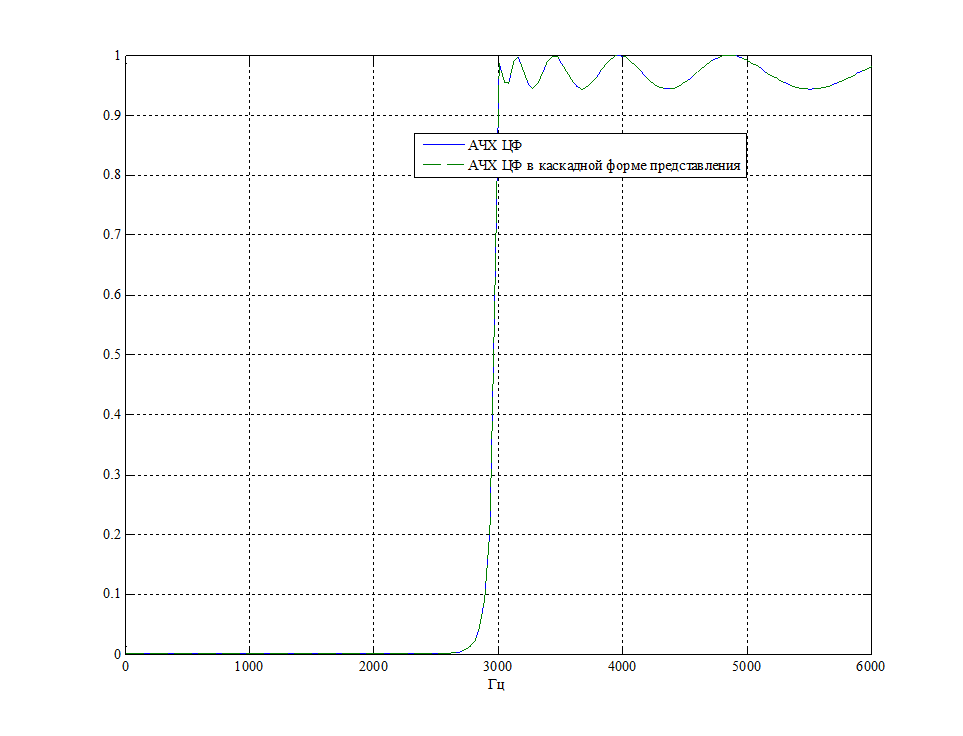
Рис. 8. АЧХ исходного ЦФ и ЦФ в каскадной форме.

Как видно из графика АЧХ исходного ЦФ и АЧХ ЦФ в каскадной форме полностью совпадают, следовательно, фильтр в каскадной форме полностью отвечает требуемой спецификации.

Тестирование фильтра.

Тестирование фильтра заключается в пропускании через него аддитивной смеси двух сигналов с различными частотами: полезного, частота которого находится в полосе пропускания, и помехи, частота которой попадает в полосу задерживания.

Фрагмент Matlab Script для тестирования фильтра:

N=500;

i=0:1:N-1;

s=2*sin(2*pi*50*i/20000);

s1=sin(2*pi*4000*i/20000);

x=s+s1;

subplot(411);

plot(i, s);

title('Сигнал помехи 50 Hz' );

subplot(412);

plot(i, s1);

title('Полезный сигнал 4000 Hz');

subplot(413);

plot(i, x);

title('Аддитивная смесь полезного сигнала и низкочастотной помехи');

subplot(414);

F=filter(numd, dend, x);

plot(i, F);

title('Отфильтрованный сигнал');

Скачать файл