Проектирование цифрового БИХ-фильтра Чебышева 1-го типа верхних частот. Вариант 1, страница 4

1.00000000000000	-2.10546875000000	1.10546875000000	1.00000000000000	0.71093750000000	0.28515625000000
1.00000000000000	-2.06250000000000	1.06250000000000	1.00000000000000	-0.28906250000000	0.58203125000000
1.00000000000000	-1.90234375000000	0.90234375000000	1.00000000000000	-0.96093750000000	0.78906250000000
1.00000000000000	-1.99609375000000	1.00000000000000	1.00000000000000	-1.28515625000000	0.89843750000000
1.00000000000000	-1.93750000000000	0.93750000000000	1.00000000000000	-1.43359375000000	0.96875000000000

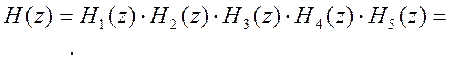
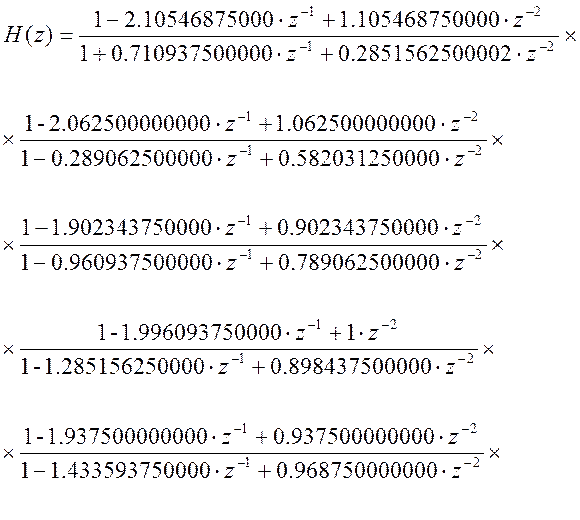
Полностью фильтр будет представлен структурной схемой вида:

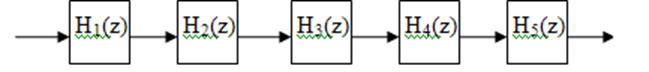
Где H₁(z),…H₅(z) – передаточные функции звеньев второго порядка

Построение АЧХ:

[numr,denr]=sos2tf(sos1,G);

[Hreal fr] = freqz(numr,denr,1024,5000);

plot(f,abs(H),':',fr,abs(Hreal),'-'),grid

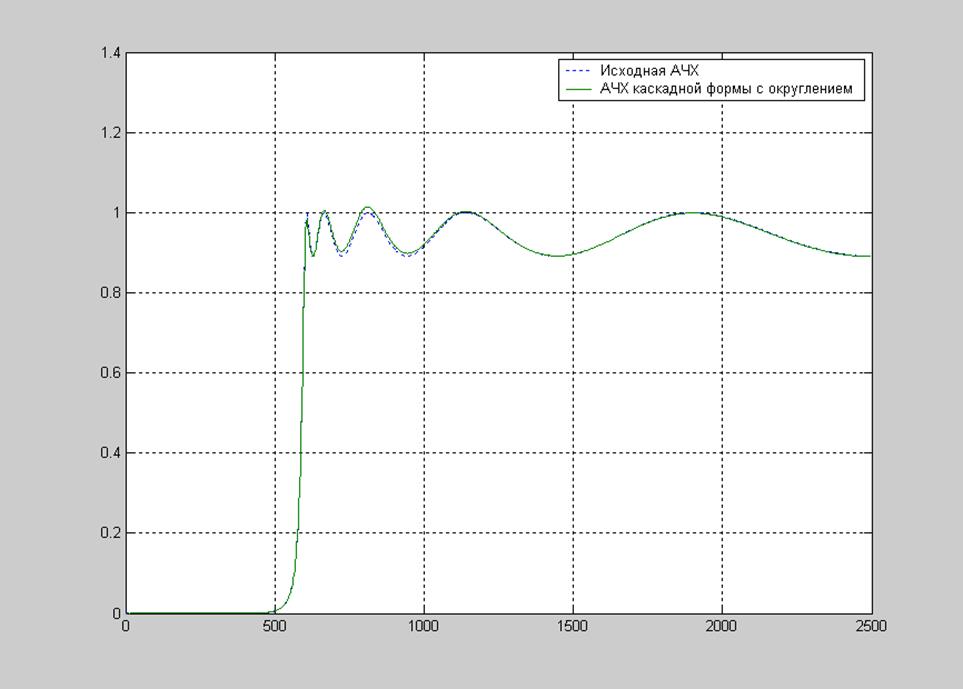
Рисунок 9. АЧХ спроектированного ФВЧ Чебышева первого типа и реализованного в каскадной форме фильтра

Глядя на графики можно судить о том, что АЧХ реализованного фильтра мало отличается от АЧХ спроектированного, таким образом подтверждается, что метод реализации фильтра был выбран верный.

6. Тестирование фильтра

Как уже упоминалось ранее, основной задачей фильтрации сигналов является определение истинной природы сигнала, а именно – выделение полезных составляющих и подавление шумов. В данном пункте рассматривается фильтрация сигнала имеющего две частотные составляющие – одна из полосы задерживания, другая – из полосы пропускания.

Для проверки работоспособности фильтра, подадим на его вход сигнал, состоящий из суммы гармоник. Одна из них будет находится на частоте из полосы пропускания фильтра, а другая – в полосе задерживания

Fs=5000;

n=0:1000;

x1=2*cos(2*pi*100*n/Fs);

x2=1*cos(2*pi*1500*n/Fs);

x=x1+x2;11

y=filter(numr,denr,x);

subplot(4,1,1)

plot(n,x1)

axis([0 500 -2 2])

subplot(4,1,2)

plot(n,x2)

axis([0 500 -2 2])

subplot(4,1,3)

plot(n,x)

axis([0 500 -3 3])

subplot(4,1,4)

plot(n,y)

axis([0 500 -2 2])

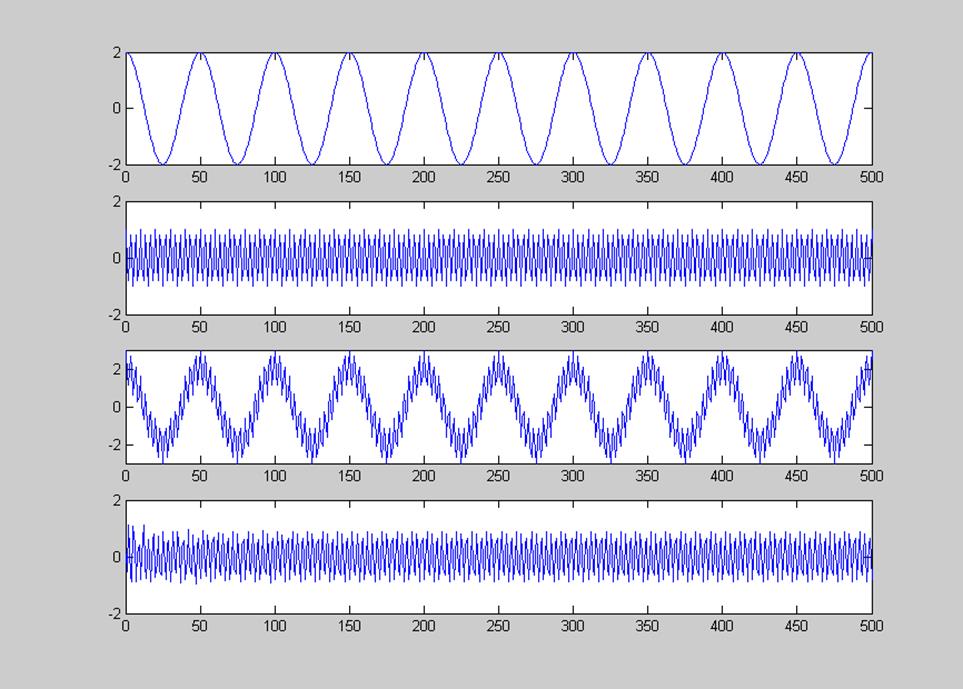
Рис. 10. Графики входного и выходного сигналов фильтра.

Результаты, представленные на графике доказывают, что фильтр пропускает составляющие сигнала с частотами из полосы пропускания и подавляет составляющие с частотами из полосы задерживания.

§  Граничная частота  полосы  пропускания - 1000 Гц,

§  Граничная частота  полосы задерживания– 800  Гц,

§  Неравномерность передачи в полосе пропускания – 0,5 дБ,

§  Минимальное ослабление в полосе задерживания – 45 дБ,

§  Частота дискретизации – 10 кГц.  

 - граничная частота полосы пропускания;

- граничная частота полосы задерживания;

 - минимальное ослабление в полосе задерживания;

- неравномерность передачи в полосе пропускания;

 - частота дискретизации.

Фильтрация сигналов из разных полос (полосы задерживания, полосы пропускания и полосы перехода )

Fs=5000;

n=0:1000;

x1=2*cos(2*pi*100*n/Fs);

x2=1*cos(2*pi*1000*n/Fs);

y1=filter(numr,denr,x2);     

y2=filter(numr,denr,x1);

x3=1*cos(2*pi*555*n/Fs);

y3=filter(numr,denr,x3);

figure(1);

subplot(2,1,1);

plot(n,x2);

axis([0 500 -2 2]);

subplot(2,1,2);

plot(n,y1);

axis([0 500 -2 2]);

figure(2);

subplot(2,1,1);

plot(n,x1);

axis([0 500 -2 2]);

subplot(2,1,2);

plot(n,y2);

axis([0 500 -2 2]);

figure(3);

subplot(2,1,1);

plot(n,x3);

axis([0 500 -2 2]);

subplot(2,1,2);

plot(n,y3);

axis([0 500 -2 2]);

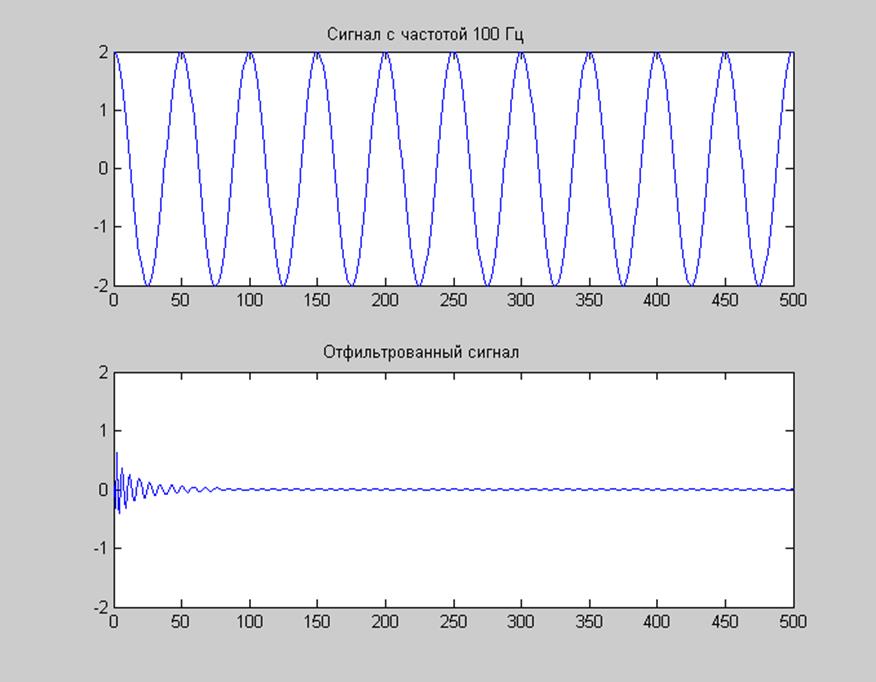
Рисунок 11. Фильтрация сигнала с частотой из полосы задерживания (100 Гц).

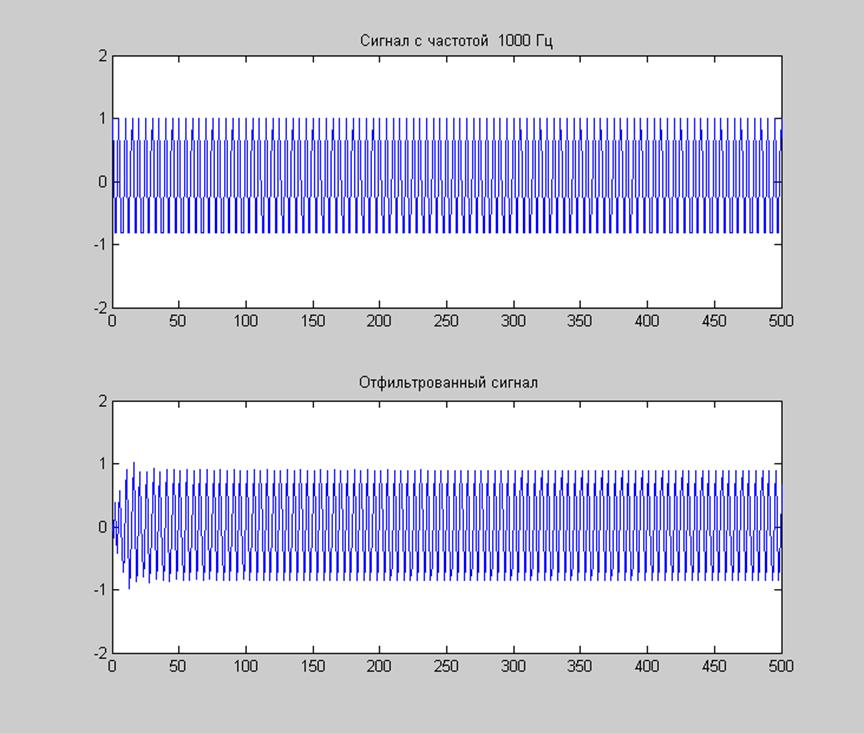
Рис. 12. Фильтрация сигнала с частотой из полосы пропускания (1000 Гц).

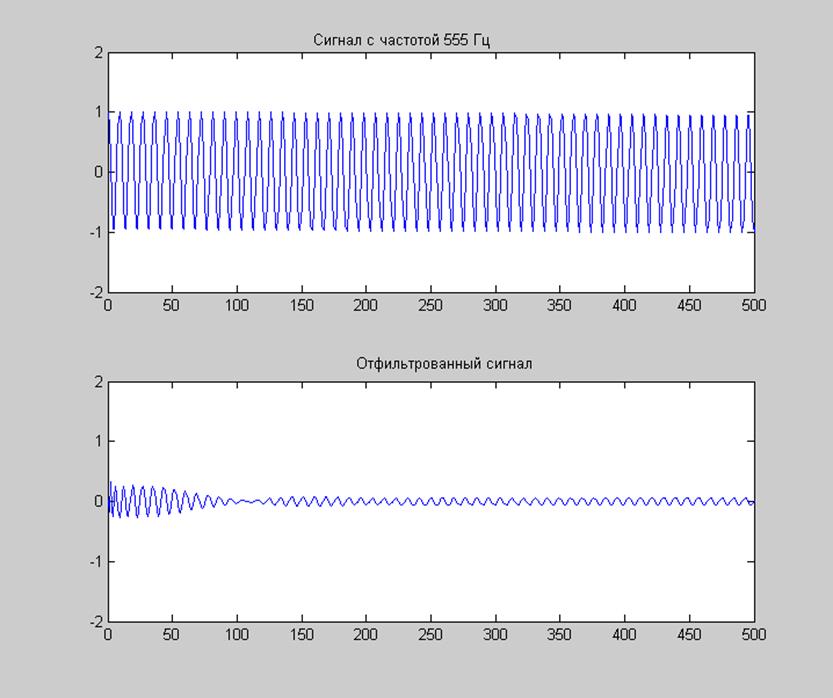
Рис. 13. Фильтрация сигнала с частотой из переходной полосы (555 Гц).

Все представленные выше графики свидетельствуют о наличии переходного процесса при осуществлении процесса фильтрации. При пропускании через фильтр сигнала с частотой из полосы пропускания, на выходе фильтра наблюдается сигнал, мало чем отличающийся от входного: происходит лишь небольшое уменьшение амплитуды и совсем незначительный сдвиг по фазе. В полосе задерживания фильтр почти полностью подавляет входной сигнал, этого вполне достаточно, чтобы получать на выходе сигнал без низкочастотных помех.

7. Программирование фильтра и оценка его быстродействия

В данной работе программирование фильтра осуществлялось на языке C++, поскольку он является одним из самых распространенных языков программирования современного мира. В качестве компилятора использовался Microsoft Visual C++ 6.0. Время фильтрации оценивалось за счет использования функции GetTickCount() библиотеки windows.

Результаты выполнения программы:

Количество отсчетов (N)	Общее время (t), мс.	Время обработки одного отсчета (Т), мкс	Максимальная частота (fmax), кГц
10000	16	1.6	625
50000	31	6.2	161
100 000	74	7.4	135
120 000	91	7.6	131

Для оценки общей f_max надо из всех экспериментов выбрать наихудший: f_max = 131 кГц – максимальная обрабатываемая частота цифровым фильтров.

при количестве отсчетов 10000 время обработки одного отсчета составляет 1.6 мкс.

 Конечно следует учитывать, что эти характеристики могут варьироваться в зависимости от технических параметров каждого конкретного компьютера.

8. Заключение