Проектирование цифрового БИХ-фильтра Чебышева 1-го типа верхних частот. Вариант 1, страница 2

В билинейном методе эта замена осуществляется следующим образом:

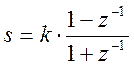                                           (1)

При преобразовании вся мнимая ось  отображается в единичную окружность, левая полуплоскость – во внутреннюю часть единичной окружности, а правая полуплоскость – во внешнюю [1]. Взаимосвязь между частотами аналогового  и цифрового  фильтров описывается выражением:

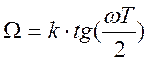                                  (2)

Чаще всего используются значения  и . Применение любого значения k приводит к одинаковым результатам.

Этапы проектирования фильтра билинейным методом:

1.   С помощью частотного преобразования определяются граничные частоты аналогового фильтра.

2.   Проектируется аналоговый нормированный фильтр нижних частот.

3.   С помощью соответствующих преобразований передаточная функция нормированного фильтра преобразуется в передаточную функцию нужного аналогового фильтра.

4.   Путем преобразования (1) осуществляется переход к передаточной функции цифрового фильтра.[1]

4. Проектирование фильтра

Параметры цифрового фильтра:

 - граничная частота полосы пропускания;

- граничная частота полосы задерживания;

 - минимальное ослабление в полосе задерживания;

- неравномерность передачи в полосе пропускания;

 - частота дискретизации.

4.1    Вычисление граничных частот аналогового фильтра:

format long; %Установка формата повышенной точности.

Fpass=600; %Граничная частота полосы пропускания

Fstop=500; %Граничная частота полосы задерживания

Ft=5000; %Частота дискретизации

Rs=40; %Минимальное ослабление в полосе задерживания.

Rp=1; %Неравномерность передачи в полосе пропускания.

%Определение Граничных Частот Аналогового Фильтра.

Ws=tan(2*pi*Fstop/(2*Ft));%Рад/Секунда

Wp=tan(2*pi*Fpass/(2*Ft));%Рад/Секунда

Ws=0.32491969623291 рад/с                                                                 

Wp=0.39592800879772 рад/c

%Проектирование нормированного фильтра нижних частот.

W=Wp/Ws;%Граничная полоса частоты задерживания

W=1.21854111458333                                                                               

4.2    Расчет нормированного фильтра верхних частот (НФНЧ):

            Характеристики НФНЧ:

Граничная частота полосы пропускания .

Граничная частота полосы задерживания:

                                        

            ; .

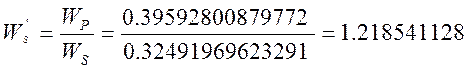
Функция [n,Wn]=cheb1ord(Wp,Ws,Rp,Rs, ‘s’) возвращает значение наименьшего порядка аналогового фильтра с потерями не более Rp в полосе пропускания и не менее Rs в полосе задерживания. Также возвращает частоту среза Wn для получения спецификаций при использовании функции cheby1.

[n,Wn]=cheb1ord(1,1.218541128 ,1,40,'s')

n = 10        Порядок фильтра                                                                

 Wn = 1      Частота среза рад/с

4.3    Определение коэффициентов передаточной функции НФНЧ:

Функция [b,a]=cheby1(N,R,Wn) осуществляет построение фильтра Чебышева нижних частот порядка N с пульсациями в полосе пропускания R децибел.     

[b,a]=cheby1(n,1,Wn,'s');                             

(8)

b = 

b0-b3	b4-b7	b8-b10
0	0	0
0	0	0
0	0	0.00383833345383
0	0

a = 

            Построение АЧХ нормированного фильтра нижних частот:

     [H,w]=freqs(b,a);

     plot(w,abs(H))

axis([0 3 0 1.1])

grid

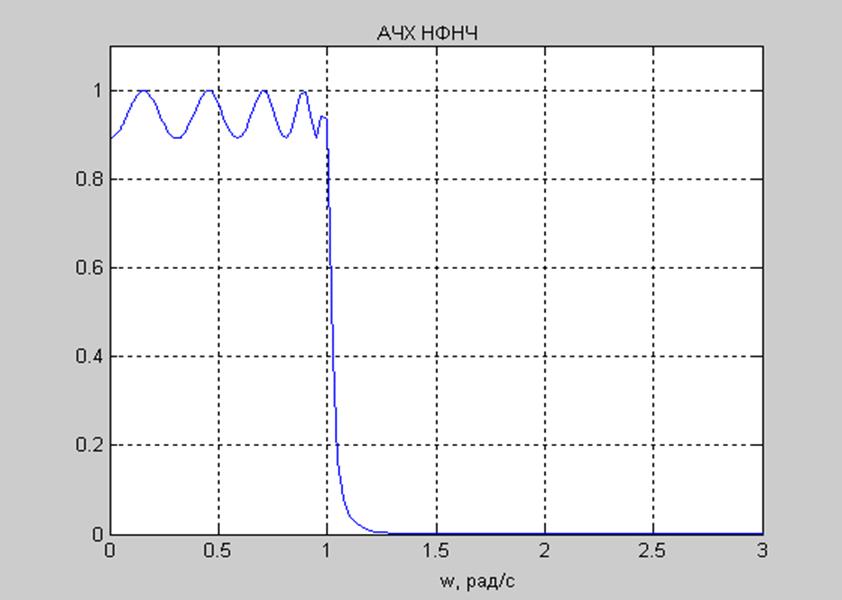
Рис. 2. АЧХ нормированного фильтра нижних частот.

Построенный график амплитудно-частотной характеристики нормированного ФНЧ полностью удовлетворяет требованиям, которые к нему предъявлялись. Колебания в полосе пропускания не превышают 0,1 (т.е.  - не превосходят -1 дБ), частота среза равна 1 рад/с.

4.4    Преобразование НФНЧ в аналоговый фильтр верхних частот:

Функция [numt,dent]=lp2hp(num,den,Wo) преобразует нормированный ФНЧ с частотой среза 1 рад/с в фильтр верхних частот с частотой среза Wo.

Wp=0.39592800879772;

[bt,at]=lp2hp(b,a,Wp)                           

bt =

bt0-bt3	bt4-bt7	bt8-bt11
0.89125093813375	-0.00000000000009	0.00000000000000
0.00000000000002	0.00000000000012	0.00000000000000
-0.00000000000000	-0.00000000000012	-0.00000000000000
0.00000000000000	0.00000000000017

at =

4.5  Преобразование аналогового фильтра в цифровой:

            Преобразование осуществляется путем подстановки в передаточную функцию аналогового фильтра верхних частот (Чебышева 1-го порядка) выражения вида (1).

     [numd,dend]=bilinear(bt,at,0.5)                   

Коэффициенты числителя передаточной функции цифрового фильтра:

numd =