Проектирование цифрового БИХ-фильтра Чебышева 1-го типа верхних частот. Вариант 1, страница 3

numd0-numd3	numd4-numd7	numd8-numd11
0.02783806429466	5.84599350187924	1.25271289325982
-0.27838064294663	-7.01519220225508	-0.27838064294662
1.25271289325984	5.84599350187921	0.02783806429466
-3.34056771535957	-3.34056771535953

Коэффициенты знаменателя передаточной функции цифрового фильтра:

dend =

dend0-dend3	dend4-dend7	dend8-dend11
1.00000000000000	6.39973607246240	0.55070825086603
-3.25681214871289	-3.91006398905721	-0.24390071235775
6.21731769254461	2.06150559369771	0.11446379563430
-7.34020840188480	-0.88974093833454

Отсюда передаточная функция:

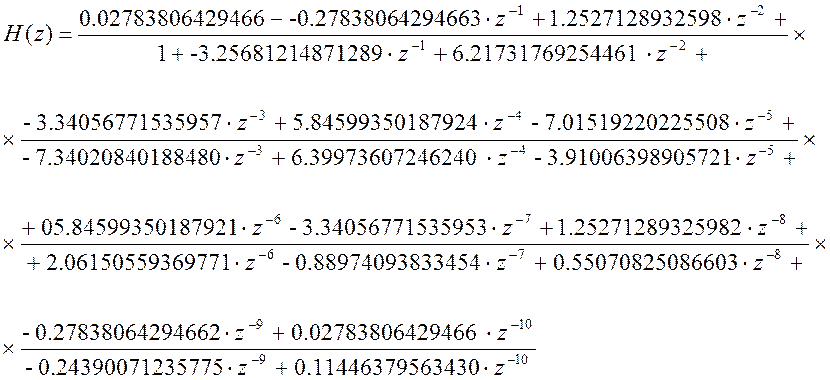
Уравнение фильтра: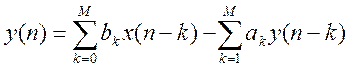

y(n) = 0.02783806429466x(n-0)-0.27838064294663x(n-1)+1.25271289325984x(n-2)- 3.34056771535957x(n-3)+ 5.84599350187924x(n-4)-7.01519220225508x(n-5)+

+5.84599350187921x(n-6)-3.34056771535953x(n-7)+  +1.25271289325982x(n-8)–0.27838064294662x(n-9)+ +0.02783806429466x(n-10)+3.25681214871289y(n-1)- 6.21731769254461y(n-2)+7.34020840188480y(n-3)-

-6.39973607246240y(n-4)+3.91006398905721y(n-5)-2.06150559369771y(n-6)+0.88974093833454y(n-7)-

0.55070825086603y(n-8)+0.24390071235775y(n-9)-

-0.11446379563430y(n-10)

4.6 Построение диаграммы нулей и полюсов фильтра:

zplane(numd, dend)

Построение диаграммы нулей и полюсов позволяет судить об устойчивости спроектированной системы. В случае непрерывных систем, для устойчивости необходимо и достаточно, чтобы действительные части всех полюсов были отрицательными. Поскольку левая полуплоскость  (отрицательные действительные значения) отображается во внутреннюю часть окружности единичного радиуса в z-плоскости, то для устойчивости дискретных систем необходимо, чтобы полюса располагались внутри этой окружности.

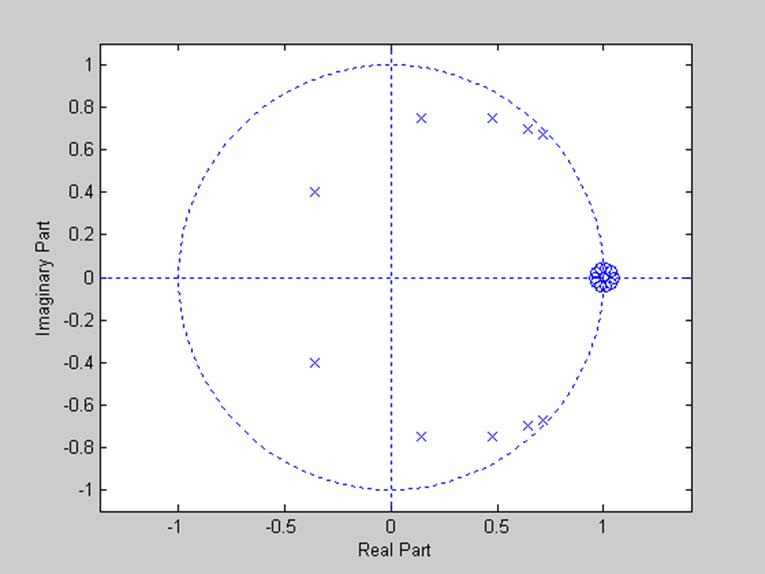
Рис. 3. Диаграмма нулей и полюсов цифрового фильтра.

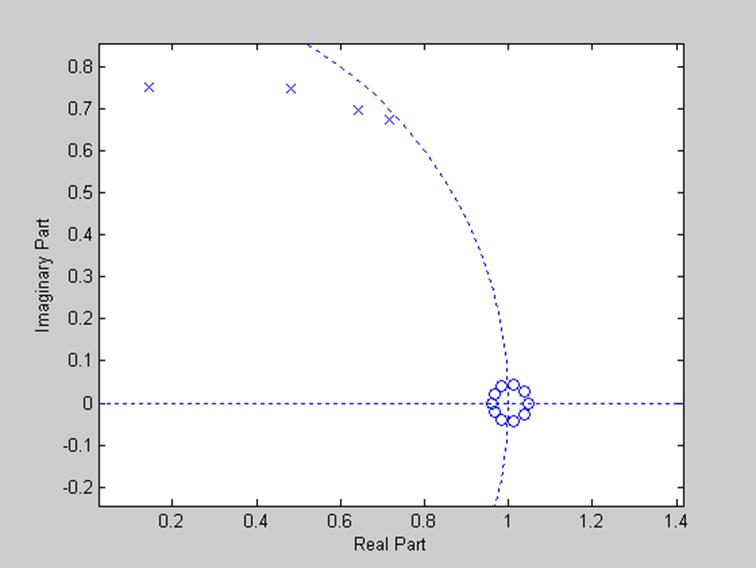
Рис. 4. Приближенный вариант диаграммы нулей и полюсов цифрового ФВЧ.

Диаграммы, представленные на рис.3-4 служат доказательством устойчивости фильтра, несмотря на то, что некоторые полюса близки к границе устойчивости. Всего на диаграммах изображено 10 нулей и 10 полюсов, что соответствует порядку фильтра.

4.7    Построение АЧХ цифрового фильтра:

[H, f] = freqz(numd, dend, 1024, Ft);

subplot(211)

plot(f, abs(H))

grid

subplot(212)

plot(f, 20*log10(abs(H)))

grid

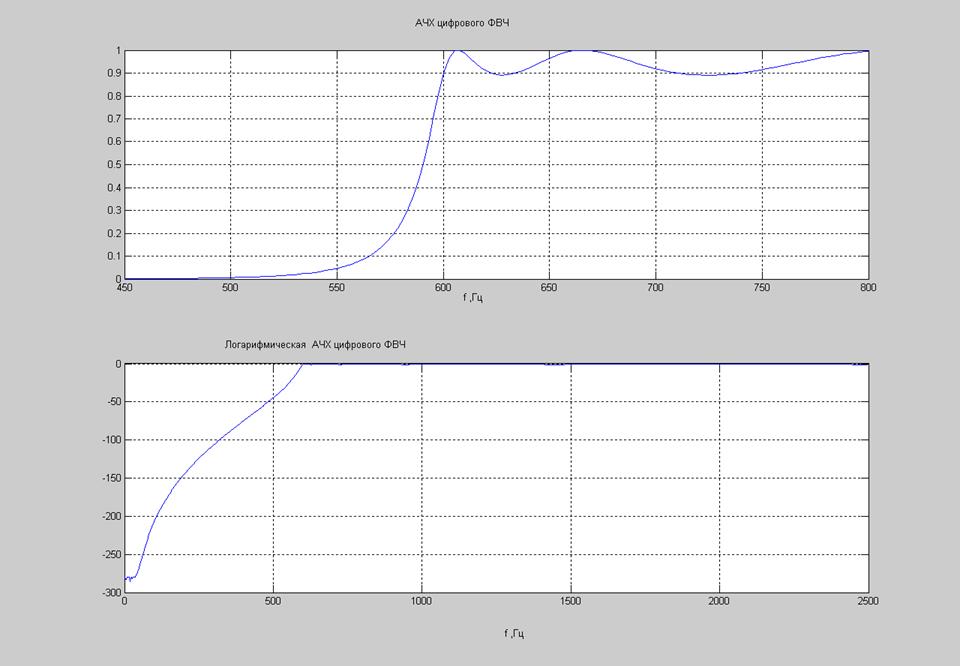
Рис. 5. Графики АЧХ и ЛАЧХ цифрового ФВЧ.

Увеличим  ЛАЧХ:

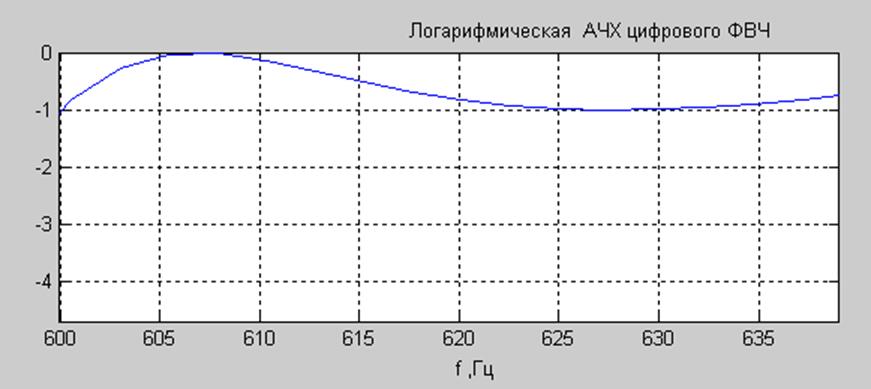
Рис. 6. Пульсации в полосе пропускания фильтра.

Пульсации в полосе пропускания фильтра не превышают требуемого значения – 1 дБ.

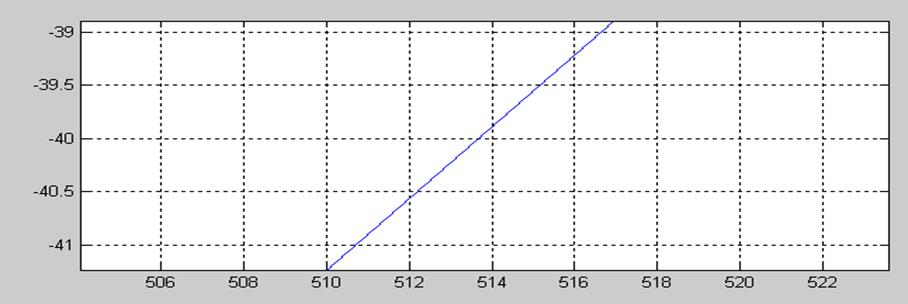
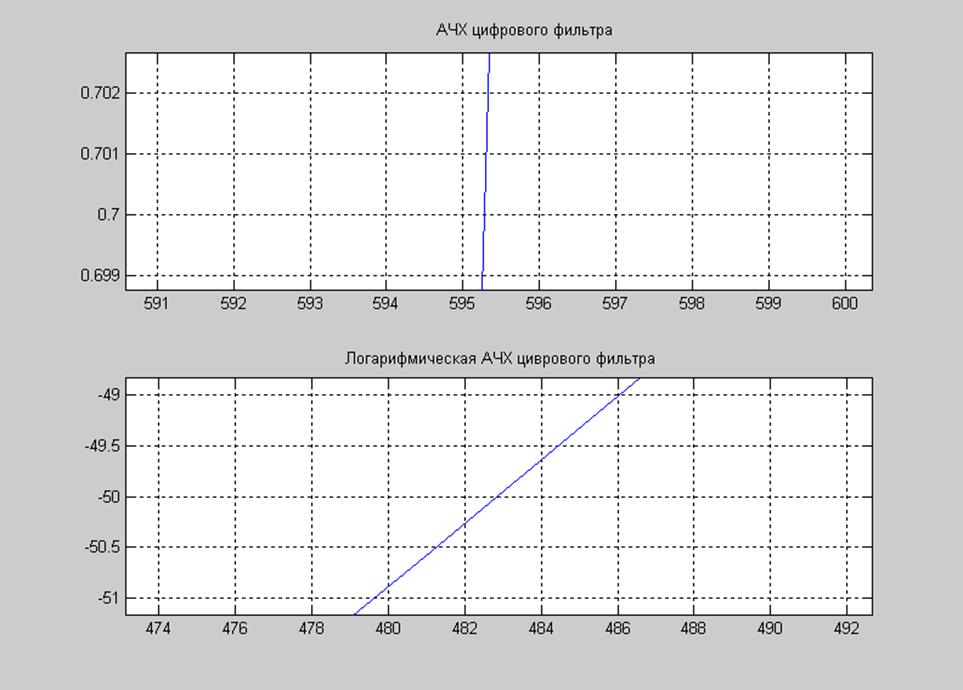
Рис. 7. График АЧХ (увеличенный) и ослабление в полосе задерживания.

Из графиков на рис.7 можно определить, что смещение граничной частоты полосы пропускания составляет 5 Гц (требуемая , спроектированная  ). Минимальное ослабление в полосе задерживания – не менее 40 дБ для всех частот до 513,5 Гц.

Из АЧХ (рис.7) видно, что пульсации наблюдаются в полосе пропускания и отсутствуют в полосе задерживания – это свойство присуще фильтрам Чебышева первого типа.
 4.8 Построение ФЧХ цифрового фильтра:

plot(f,unwrap(angle(H)))

grid

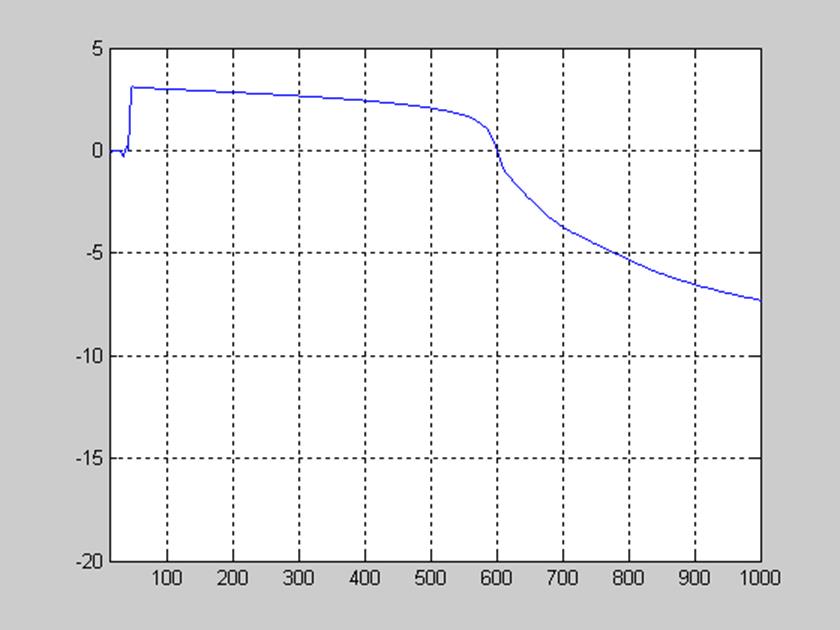
Рис. 8. Фазочастотная характеристика цифрового ФВЧ Чебышева 1-го типа.

Фазочастотная характеристика не является линейной. В границах полосы пропускания (от 600 Гц) функция убывает гораздо быстрее, чем в полосе задерживания и переходной полосе. 

5. Реализация фильтра

При проектировании принимается предположение о возможности реализации фильтра с любыми коэффициентами. Но в действительности из-за конечной разрядности процессоров производится округление коэффициентов, что несомненно приводит к нежелательным последствиям: смене положения нулей и полюсов на z-плоскости и как следствие – изменению частотных характеристик фильтра, а возможно и приведению фильтра в неустойчивое состояние (что весьма возможно для данной работы, где некоторые из полюсов находятся вблизи границы устойчивости). Поэтому необходимо достаточно тщательно  осуществлять подбор формы реализации фильтра.

Существует множество способов реализации БИХ-фильтров. Но чаще остальных используются следующие:

·  прямая,

·  каскадная

·   параллельная формы.

Прямая форма подразумевает под собой непосредственное представление передаточной функции фильтра.

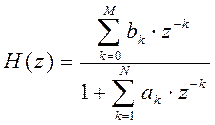
«Такая форма реализации дает приемлемую точность для ФНЧ и ФВЧ порядка не выше 10» [1], поэтому в данной работе она не будет использоваться.

 При параллельной форме передаточная функция представляется в виде суммы передаточных функций первого или второго порядка:

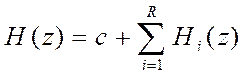, где .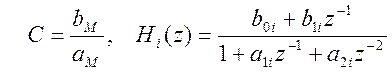

Но при синтезе фильтров на основе билинейного преобразования предпочтительнее использовать каскадную (последовательную) форму реализации [1].

Каскадная форма реализации:

Для цифрового фильтра передаточную функцию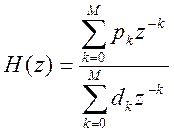 можно представить в виде:

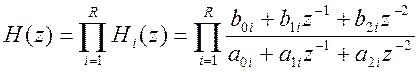, где .         (3)

Эта форма реализации фильтра более устойчива к ошибкам квантования и погрешностям округления.

Порядок фильтра, проектируемого в данной работе – 10, поэтому передаточная функция будет представлена в виде пяти  звеньев второго порядка.

Функция [sos,G]=tf2sos(b,a) предназначена для представления передаточной функции, описанной числителем b и знаменателем a, в виде звеньев второго порядка.

 [sos,G]=tf2sos(numd,dend);

 sos1=round(sos*256)/256;          %округление до 8 бит

sos1 =