


Министерство общего и профессионального образования Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра систем сбора и обработки данных
Дисциплина «Теория и обработка сигналов»
(5 - й семестр)
Расчетно-графическая работа
Выполнила: Преподаватель:
Группа: АТ-53 Щетинин Ю.И.
Студентка: Литвинцева Ю.В.
Шифр: 010805306
НОВОСИБИРСК
2007
Раздел 1
1.6. Нахождение периода сигнала
![]()
Сумма
двух периодических сигналов ![]() , где x1(t) и x2(t)
–периодические сигналы с периодами T1 и Т2 соответственно, является также
периодическим сигналом с периодом, равным наименьшему общему кратному T1 и Т2.
Пусть
, где x1(t) и x2(t)
–периодические сигналы с периодами T1 и Т2 соответственно, является также
периодическим сигналом с периодом, равным наименьшему общему кратному T1 и Т2.
Пусть 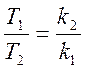 , положим
, положим ![]() .
Для периодического сигнала
.
Для периодического сигнала
![]() .
.
Для
сигнала cos(6t) ![]() ,
для сигнала sin(8t)
,
для сигнала sin(8t) ![]() ,
, 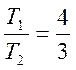 . Поэтому период их суммы
. Поэтому период их суммы ![]()
Ответ: Период T = π.
1.7. Исследование характера
поведения экспоненциального сигнала дискретного времени ![]() при комплексных значениях
при комплексных значениях ![]() .
.
![]()
Используя формулу Эйлера ![]() , функцию x[n] можно выразить в виде
, функцию x[n] можно выразить в виде ![]() .
.
Данный комплексный
периодический сигнал имеет период 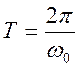 , действительная и
мнимая части – гармоники с частотой
, действительная и
мнимая части – гармоники с частотой ![]() .
.
Если ![]() <1,
то в области положительных значений n амплитуда функции будет
затухающей. В области отрицательных значений, наоборот – возрастающей. Если
<1,
то в области положительных значений n амплитуда функции будет
затухающей. В области отрицательных значений, наоборот – возрастающей. Если ![]() >1, то функция затухает в области
отрицательных значений, возрастает в положительной области.
>1, то функция затухает в области
отрицательных значений, возрастает в положительной области.
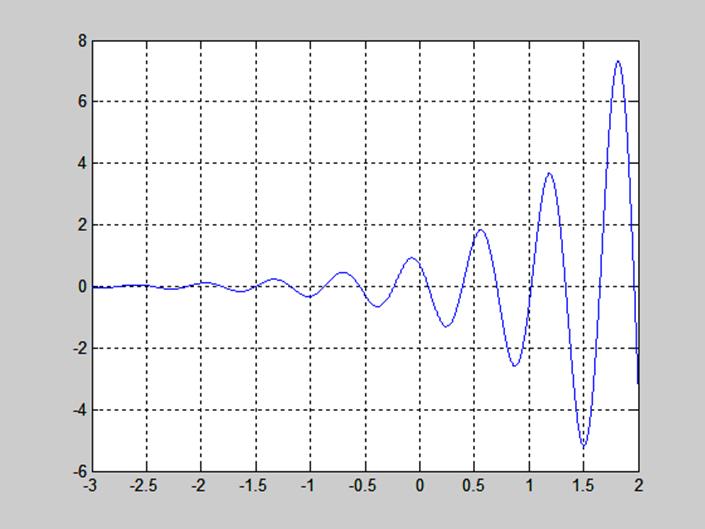
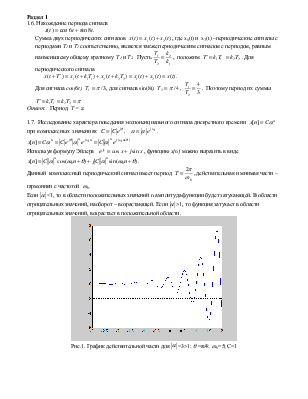
Рис.1. График действительной части для ![]() =3>1;
=3>1; ![]() =π/4;
=π/4;
![]() =5; С=1
=5; С=1
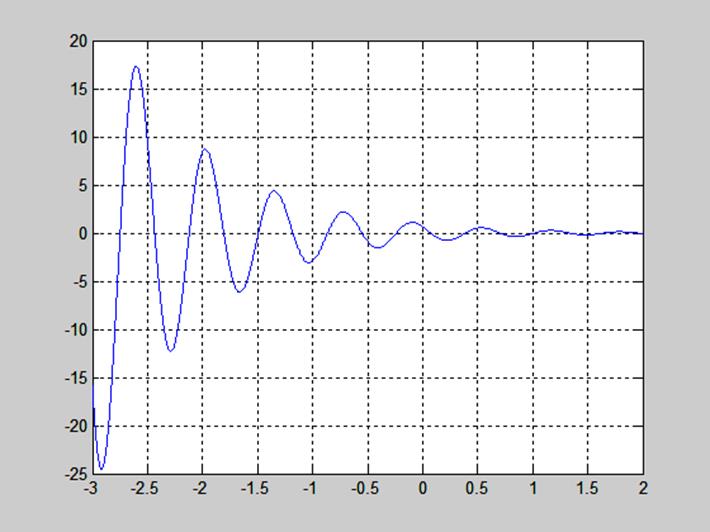
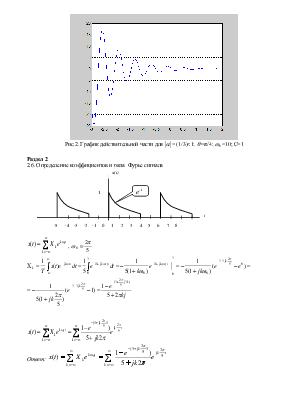
Рис.2. График действительной части для ![]() = (1/3)<1;
= (1/3)<1; ![]() =π/4;
=π/4;
![]() =10; С=1
=10; С=1
Раздел 2
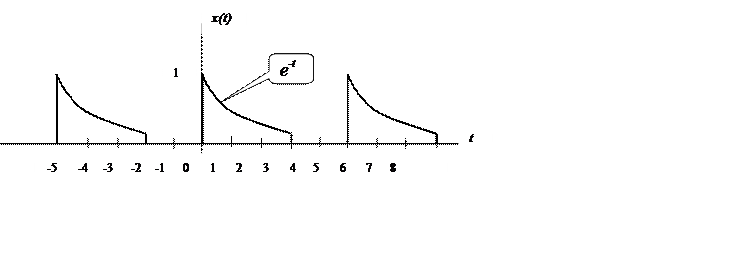 2.6.
Определение коэффициентов и ряда Фурье сигнала
2.6.
Определение коэффициентов и ряда Фурье сигнала
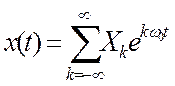 ,
, 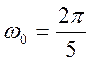
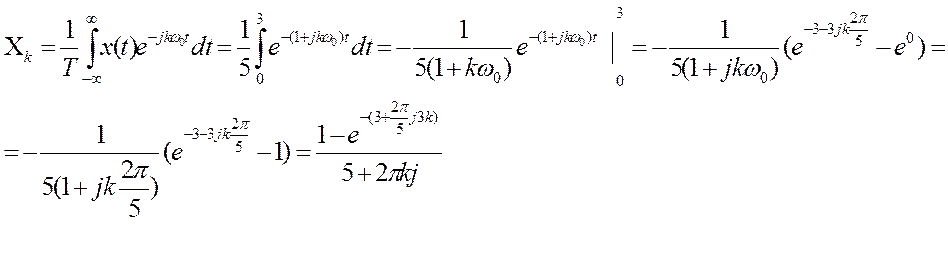
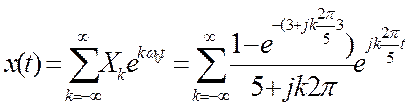
Ответ: 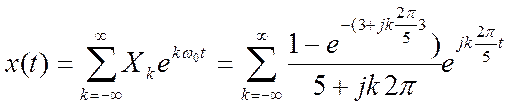
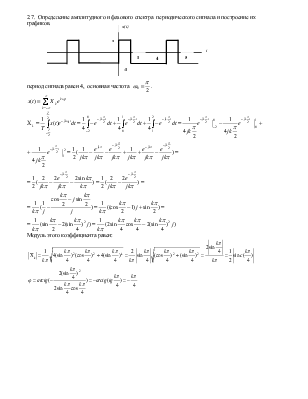
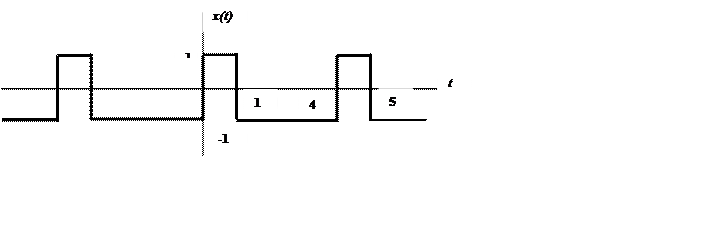 2.7.
Определение амплитудного и фазового спектра периодического сигнала и
построение их графиков.
2.7.
Определение амплитудного и фазового спектра периодического сигнала и
построение их графиков.
период сигнала равен 4,
основная частота 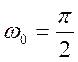 .
.
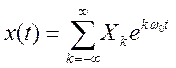
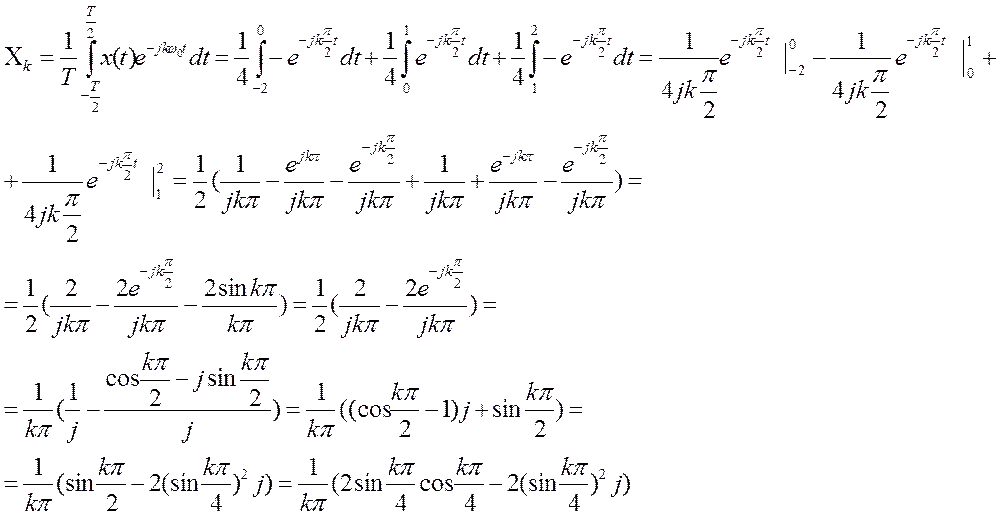
Модуль этого коэффициента равен:
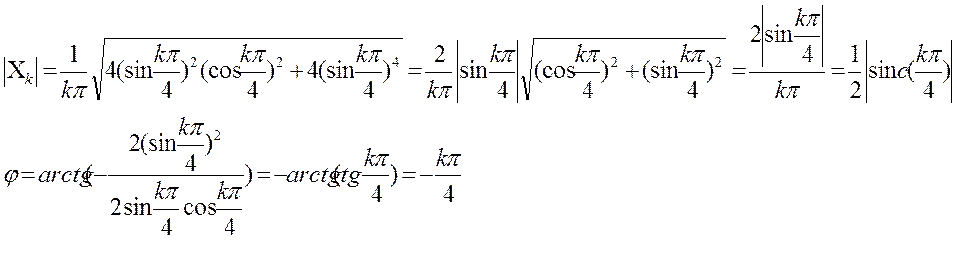
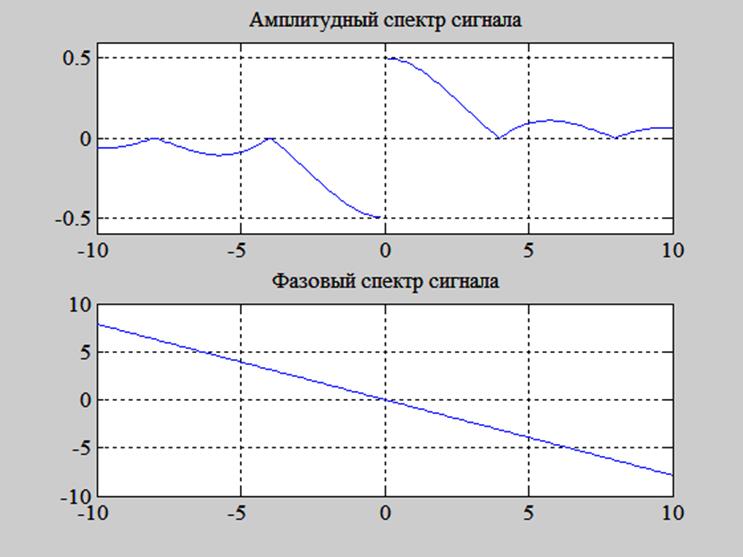
Рис. 3. Графики амплитудного и фазового спектров сигнала.
Раздел 3.
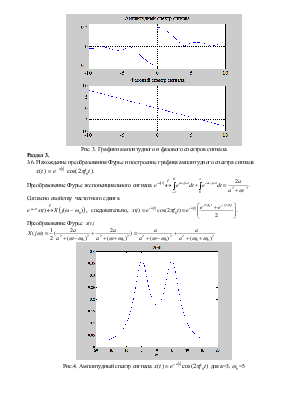
3.6. Нахождение преобразования Фурье и построение графика амплитудного спектра сигнала
![]()
Преобразование Фурье
экспоненциального сигнала 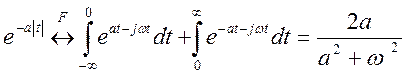 .
.
Согласно свойству частотного сдвига
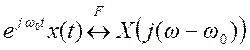 ,
следовательно,
,
следовательно, 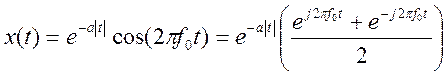 .
.
Преобразование Фурье x(t)
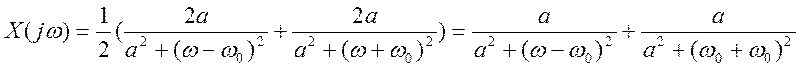
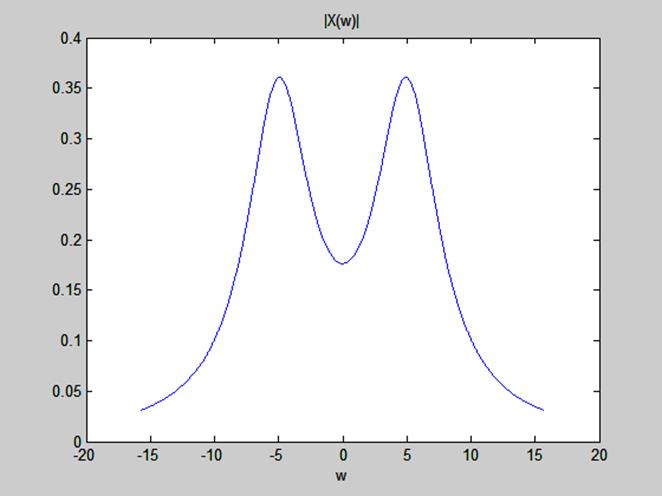
Рис.4. Амплитудный спектр сигнала ![]() для а=3,
для а=3, ![]() =5
=5
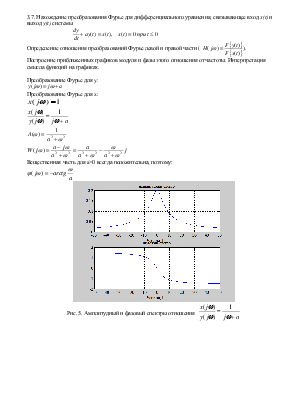
3.7. Нахождение
преобразования Фурье для дифференциального уравнения, связывающее вход x(t) и выход y(t) системы
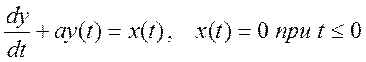
Определение отношения
преобразований Фурье левой и правой части ( 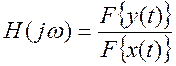 ).
).
Построение приближенных графиков модуля и фазы этого отношения от частоты. Интерпретация смысла функций на графиках.
Преобразование Фурье для y:
![]()
Преобразование Фурье для x:
![]()
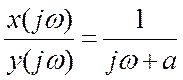
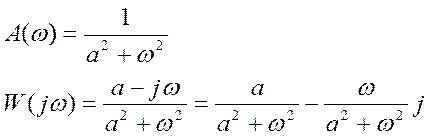
Вещественная часть для a>0 всегда положительна, поэтому:
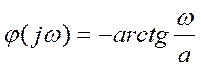
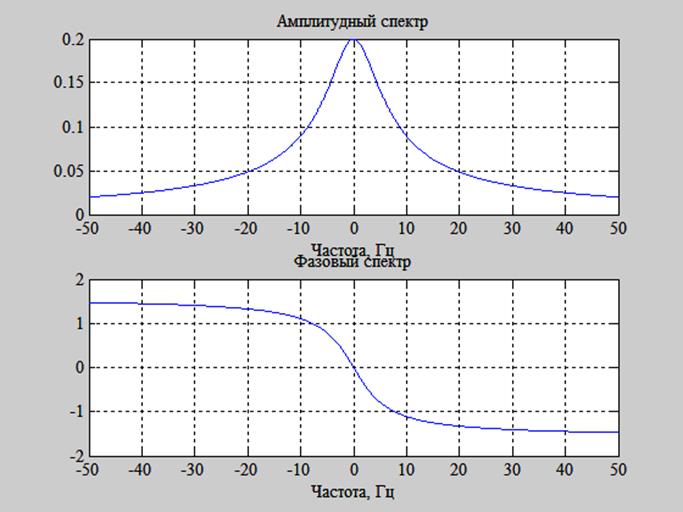
Рис. 5. Амплитудный и фазовый спектры отношения 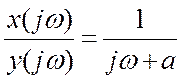
Раздел 4.
4.6.
Докажем, что для действительной последовательности x[n] амплитудный спектр 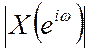 является
четной функцией от ω, а фазовый спектр
является
четной функцией от ω, а фазовый спектр ![]() -
нечетной функцией от ω.
-
нечетной функцией от ω.
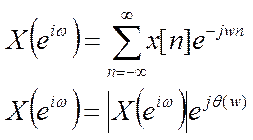
Сигнал x[n] можно представить в виде суммы четной и нечетной составляющей:
x[n]=xe[n]+xo[n], где первая – это четная составляющая, а вторая – нечетная.
Подставим это выражение в первую формулу:
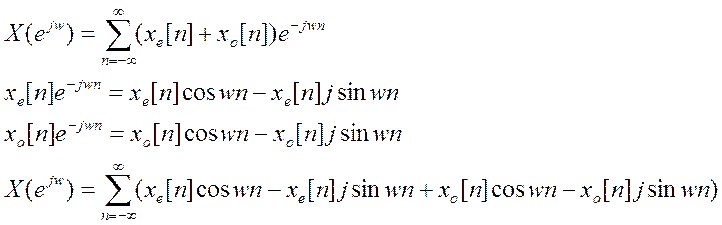
Поскольку бесконечная сумма нечетной функции равна 0, запишем это равенство в следующем виде:
![]()
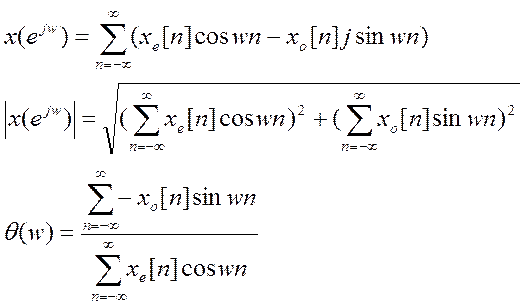
Для выражения амплитудного спектра видно, что под корнем получается четная функция, а значит и сам корень является четной функцией.
Для фазового спектра - так как в сумму числителя входит sin, то функция является нечетной.
4.7. Найдите вид сигнала x[n], ДВПФ которого
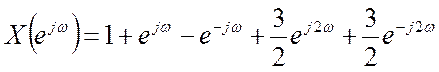 .
.
Из формулы для прямого ДВПФ:
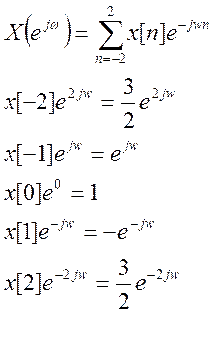
Непосредственное сравнение левой и правой части дает:
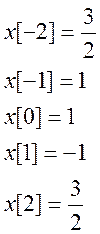 Отсюда
Отсюда ![]()
Ответ. x[-2]=1,5, x[-1]=1, x[0]=1, x[1]= -1, x[2]=1,5.
Раздел 5.
5.6. Вычисление свертки сигналов. Построение графика свертки.
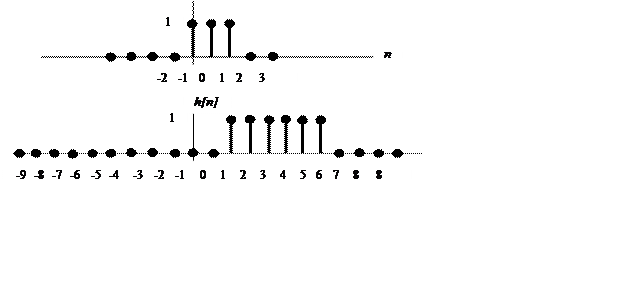 |
Используя свойство свертки
ДПФ, запишем: 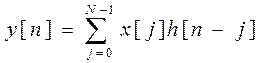
Вычислим свертку x[n] и
h[n] для 0![]() n
n ![]() 9:
9:
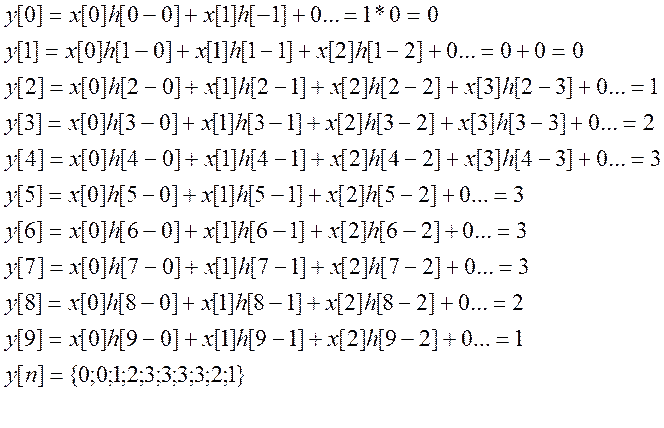
В итоге y[n]= 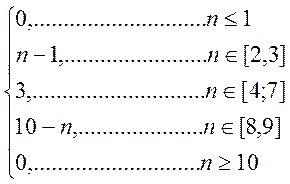
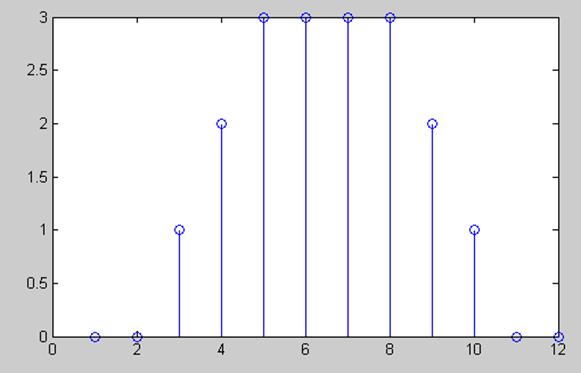
Рис. 6. График свертки x[n] и h[n].
Ответ: 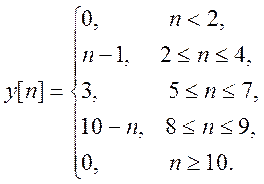
5.7.
Вычисление свертки двух непрерывных сигналов и построение её графика
В соответствии с геометрическим смыслом операция свертки заключается в зеркальном отражении одной из участвующих в свертке функций, сдвиге её на значение t, перемножении операндов и интегрировании результата перемножения.
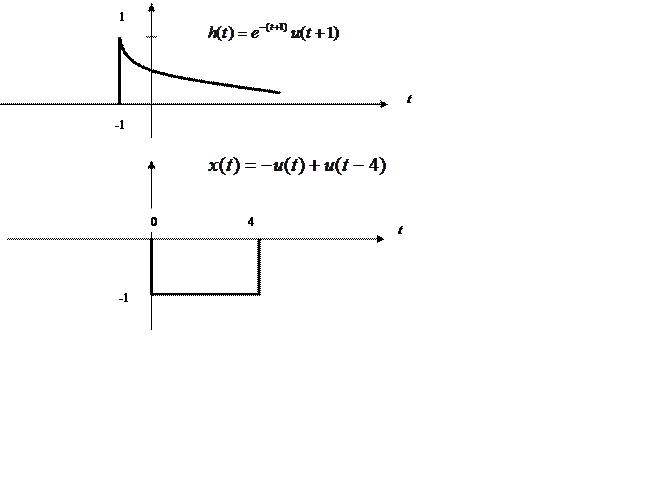 |
|||
 |
|||
Интервал интегрирования при этом разбивается на следующие подинтервалы:
1) t<-1, при этом x(τ) и h(t-τ) не перекрываются и выходной сигнал y(t)=0.
2)
![]() ,
x(τ), h(t-τ) перекрываются на интервале
,
x(τ), h(t-τ) перекрываются на интервале ![]()
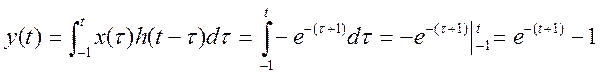
3)
![]()
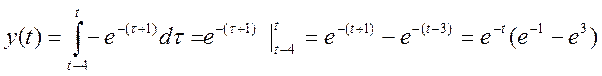
Таким образом, результат свертки:
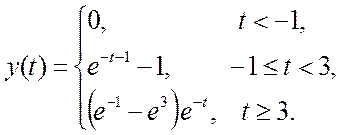
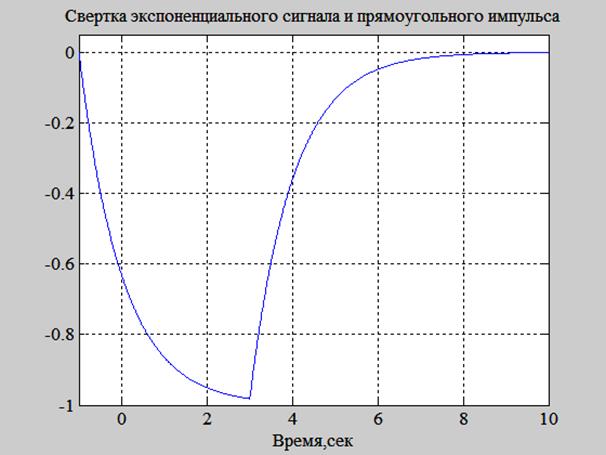
Рис. 7. График свертки сигналов h(t) и x(t).
Ответ. 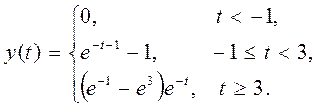
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.