





НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов»
РАССЧЕТНО ГРАФИЧЕСКОЕ ЗАДАНИЕ
Вариант составлен индивидуально.
Группа: АТ-73 Преподаватель: Щетинин Ю.И.
Студент: Засыпкин Г.Е.
Новосибирск
2010
1. Дискретный по времени сигнал имеет вид
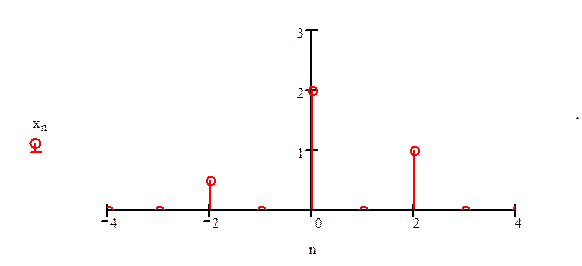
Найдите x[4-2n].
Решение :
Преобразуем x[4-2n] и получим x[-2(n-2)].
Для n= 3, y[3]=x[-2]= 0.5;
Для n = 2, y[2]=x[0]=2;
Для n = 1, y[1]=x[2]=1;
Для n = 0 y[0]=x[4]=0.
Таким образом график y= x[4-2n] имеет вид:
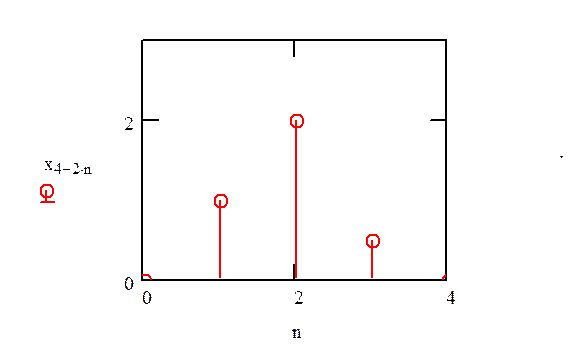
Рис.1. График преобразованного сигнала.
2.
Определите, является ли линейной, стационарной (инвариантной во
времени) и Система является линейной, если для неё справедлив принцип
суперпозиции: Определите, является ли линейной, стационарной (инвариантной во
времени) и устойчивой система- интегратор с уравнением 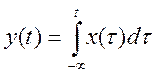 ?
?
Решение:
Система является линейной, если для неё справедлив принцип суперпозиции:
Если ![]() , то
, то 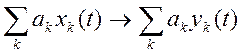
Проверим, линейна ли заданная система.
Пусть при ![]()
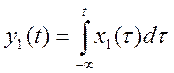 и при
и при ![]()
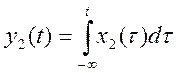 .
.
Если ![]() , то
, то
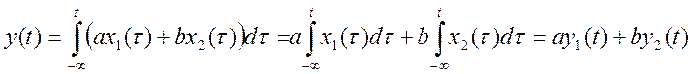 , значит, система линейна.
, значит, система линейна.
Система является стационарной (инвариантной во времени), если временной сдвиг сигнала на входе вызывает такой же сдвиг сигнала на выходе системы.
Проверим, стационарна ли заданная система.
Если ![]() , то
, то
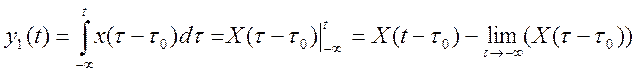
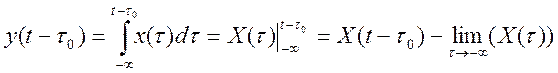
![]() ,значит, система
стационарна.
,значит, система
стационарна.
Система неустойчива система, т.к., если ![]() , то выходной сигнал неограниченно
возрастает с увеличением времени интегрирования t.
, то выходной сигнал неограниченно
возрастает с увеличением времени интегрирования t.
Ответ. Система - линейная, инвариантная во времени, но неустойчивая.
3.
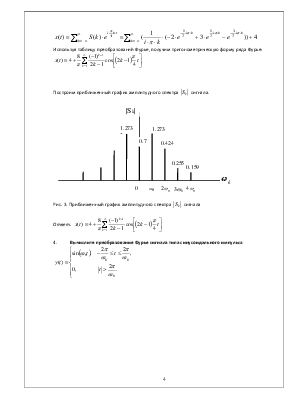
Разложите в ряд Фурье сигнал
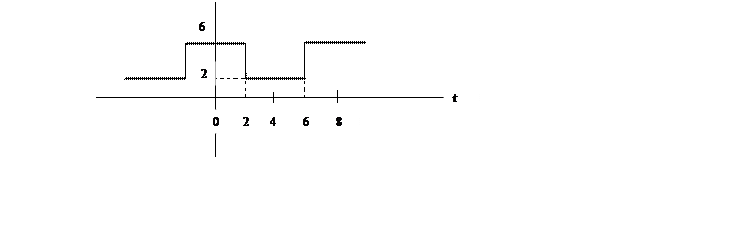
Рис.2. Сигнал.
и постройте его амплитудный спектр.
Функция периодическая с периодом T = 8 и угловой частотой:
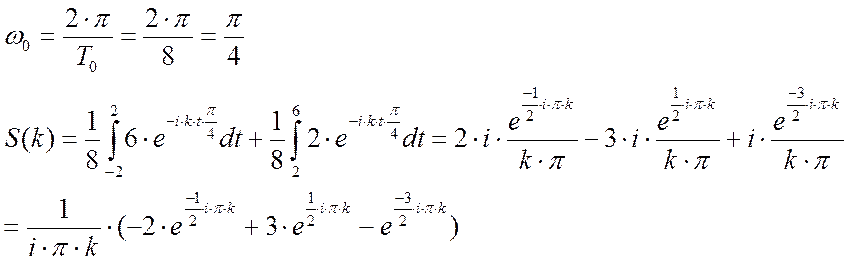
Запишем комплексный ряд Фурье:
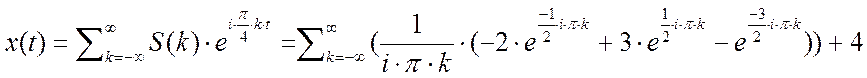
Используя таблицу преобразований Фурье, получим тригонометрическую форму ряда Фурье:
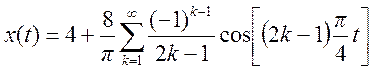
Построим
приближенный график амплитудного спектра ![]() сигнала.
сигнала.
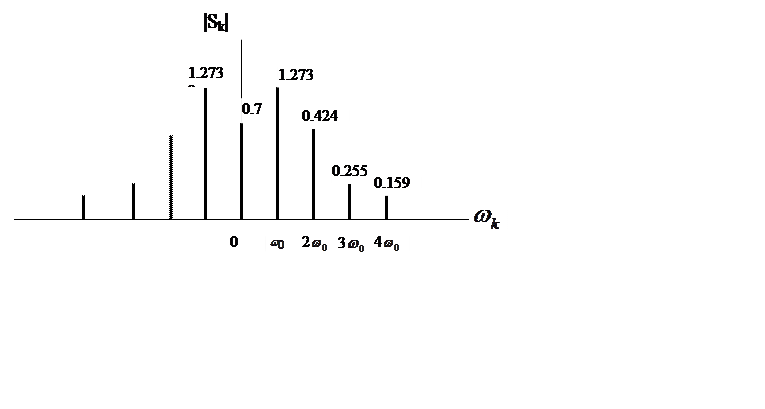
Рис.
3. Приближенный график амплитудного спектра ![]() сигнала
сигнала
Ответ. 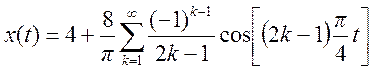
4.
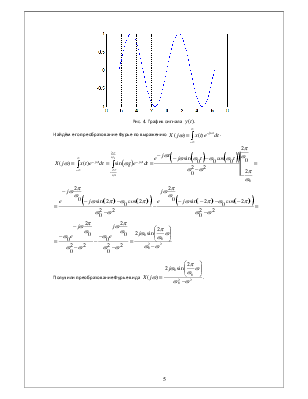
Вычислите преобразование Фурье сигнала типа синусоидального импульса
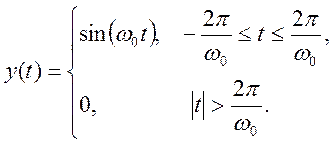
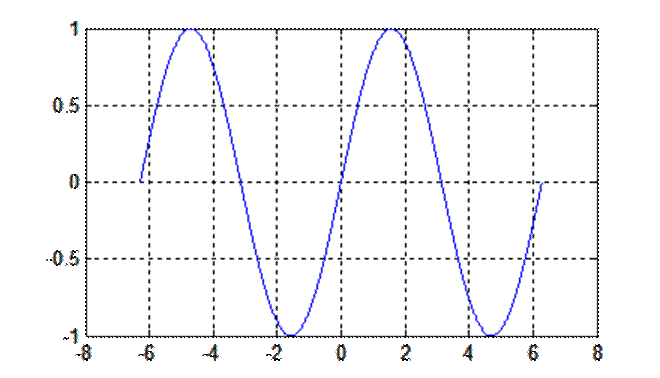
Рис. 4. График сигнала ![]() .
.
Найдём его
преобразование Фурье по выражению 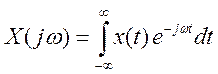 .
.
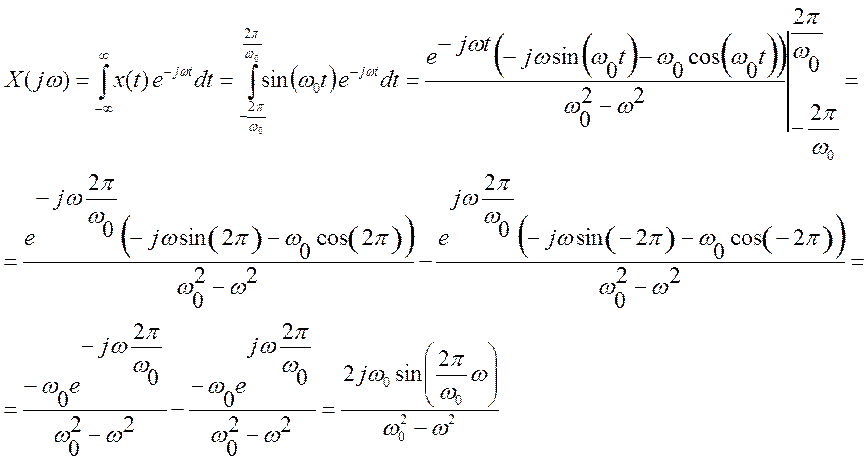
Получили
преобразование Фурье вида 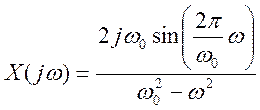 .
.
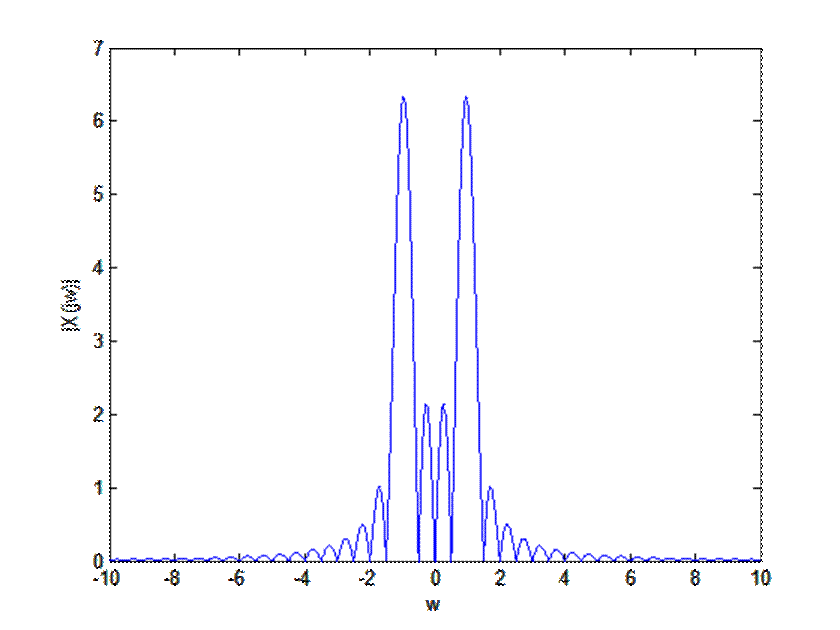
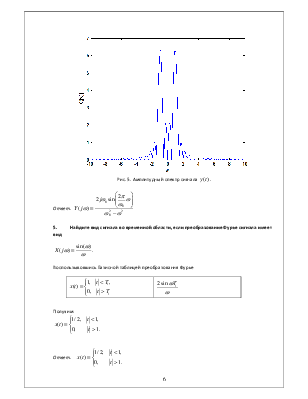
Рис. 5. Амплитудный спектр сигнала ![]() .
.
Ответ. 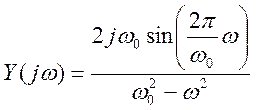
5. Найдите вид сигнала во временной области, если преобразование Фурье сигнала имеет вид
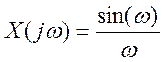 .
.
Воспользывовшись Базисной таблицей преобразования Фурье
|
|
|
Получим:
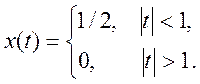
Ответ. 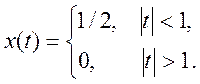
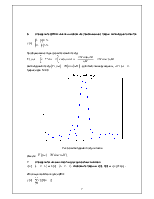
6. Определите ДВПФ сигнала и изобразите (приближенно) график амплитудного спектра
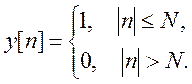
Преобразование Фурье (комплексный спектр)
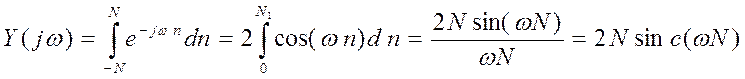
Амплитудный
спектр ![]() - действительная функция ω,
- действительная функция ω, ![]() .
.
Графики для N=0.5:
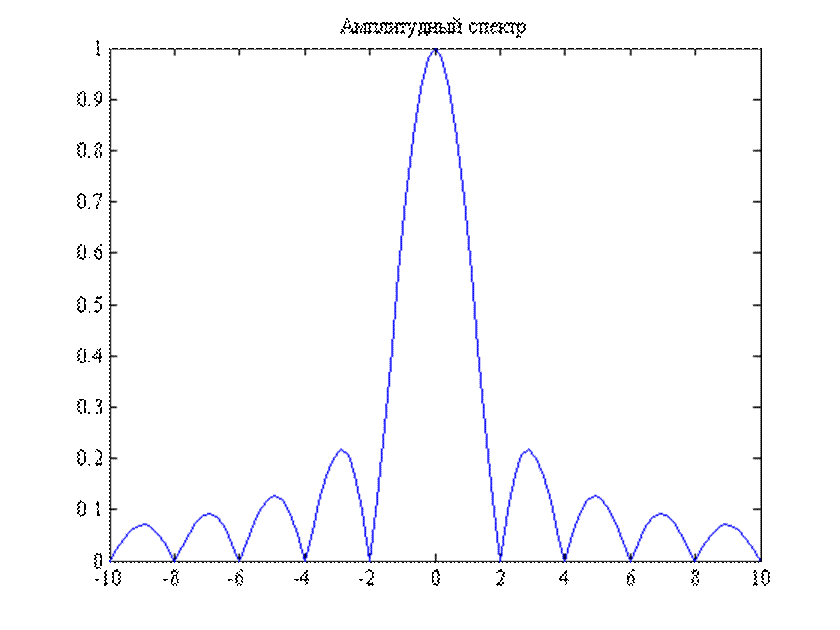
Рис.6. Амплитудный спектр сигнала
Ответ: ![]() .
.
7.
Определите значения свертки двух дискретных сигналов:
![]() и
и ![]() .
Изобразите графики x[n], h[n] и
.
Изобразите графики x[n], h[n] и ![]() .
.
Используя свойство свертки ДПФ:
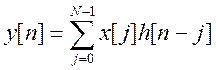
Вычислим свертку x[n] иh[n] :
y[0]=1*3=3
y[1]=1*2+2*3=8
y[2]=1*1+2*2+3*3=14
y[3]=2*1+3*2=8
y[4]=3*1=3
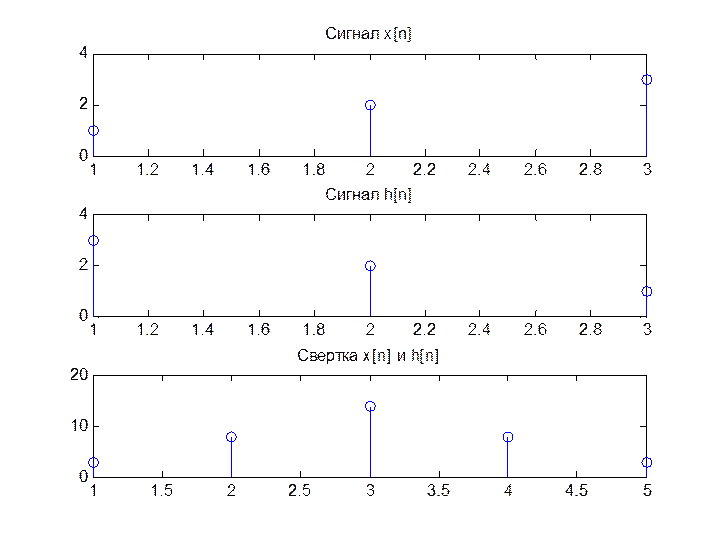
Рис.7. Графики сигналов и их свертки.
Ответ: y = { 3, 8, 14, 8, 3}.
8.
Сигнал x(t)
со спектральной плотностью ![]() дискретизируется
с интервалом отсчетов, равным 100 мкс. Возможно ли полное восстановление
сигнала по его отсчетам?
дискретизируется
с интервалом отсчетов, равным 100 мкс. Возможно ли полное восстановление
сигнала по его отсчетам?
Сигнал x(t) со спектральной
плотностью ![]() дискретизируется с интервалом
отсчетов, равным 100 мкс.
дискретизируется с интервалом
отсчетов, равным 100 мкс.
Определим возможно ли полное восстановление сигнала по его отсчетам.
Согласно
теореме отсчётов, если сигнал не имеет спектральных составляющих с частотами
выше fm, то он полностью
определяется своими отсчетами в дискретные моменты времени через интервал
отсчетов 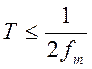 .
.
Спектральная
плотность заданного сигнала x(t) ![]() ,
т.е. сигнал не имеет спектральных составляющих с частотами выше
,
т.е. сигнал не имеет спектральных составляющих с частотами выше 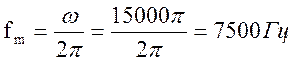 .
.
Значит,
данный сигнал полностью определяется отсчётами, взятыми в дискретные моменты
времени через интервал отсчетов 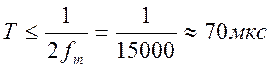 .
.
По
условию, дискретизация проводится с интервалом отсчётом ![]() ,
следовательно, сигнал не может быть точно восстановлен по отсчётам.
,
следовательно, сигнал не может быть точно восстановлен по отсчётам.
Ответ: Сигнал не может быть восстановлен по отсчетам.
9.
Сигнал
x(t) имеет
синусоидальные компоненты с частотами f1 = 250, f2 = 450,
f3 = 1000 Гц. Этот сигнал
преобразуется в дискретный с частотой отсчетов FS = 1,5 кГц. После
дискретизации сигнал восстанавливается с помощью ФНЧ с частотой среза 750
Гц. Определите частотные компоненты восстановленного сигнала.
Определим частотные компоненты восстановленного сигнала.
Согласно теореме отсчётов сигнал точно восстанавливается по
своим отсчётам, если они взяты с частотой ![]() .
При частоте отсчетов Fs максимально
возможная частота синусоиды
.
При частоте отсчетов Fs максимально
возможная частота синусоиды 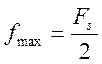 .
.
В данной задаче 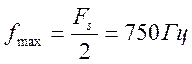 .
Значит, синусоидальные компоненты сигнала с частотами f1
= 250 и f2 = 450 Гц могут быть
точно восстановлены по отсчётам, взятым с частотой FS
= 1,5 кГц.
.
Значит, синусоидальные компоненты сигнала с частотами f1
= 250 и f2 = 450 Гц могут быть
точно восстановлены по отсчётам, взятым с частотой FS
= 1,5 кГц.
Но компонента с частотой ![]() не может быть точно
восстановлена и происходит свёртывание данной гармоники относительно частоты
не может быть точно
восстановлена и происходит свёртывание данной гармоники относительно частоты ![]() и частота
и частота ![]() подменяется частотой 500 Гц.
подменяется частотой 500 Гц.
Таким образом, получили, что в выходном сигнале будут присутствовать синусоидальные составляющие с частотами 250, 450, 500 Гц.
Ответ: в выходном сигнале будут присутствовать синусоидальные
составляющие с частотами 250, 450, 500 Гц.
10. Определите передаточную функцию, полюса, АЧХ и ФЧХ RLC – цепи, изображенной на рис.
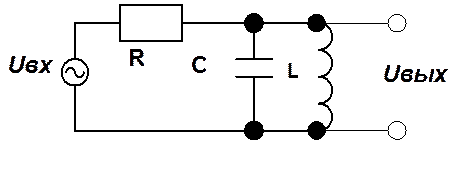
![]()
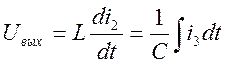
![]()
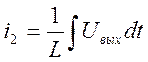 и
и 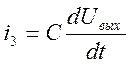
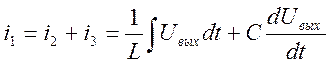
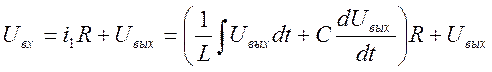
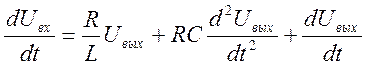
Возьмём преобразование Лапласа от обеих частей полученного уравнения.
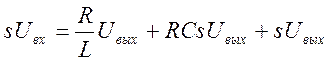
Найдём передаточную функцию
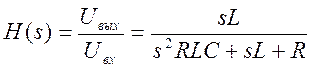
Примем значения параметров схемы равными:
R = 1 Ом
L = 1 Гн
C = 1 Ф
Передаточная функция при данных значениях параметров примет вид:
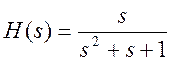
Найдём полюса (корни знаменателя) передаточной функции
![]()
Решая данное уравнение, получим полюса передаточной функции:
![]()
Действительные части полюсов отрицательны, значит, система устойчива.
Найдём АЧХ и ФЧХ RLC – цепи.
Частотная характеристика заданной цепи:
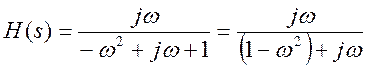
Выделим вещественную и мнимую части.
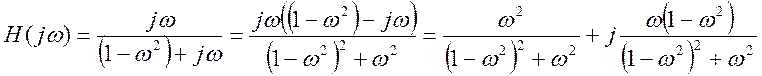
АЧХ:
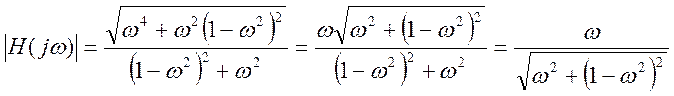
ФЧХ:
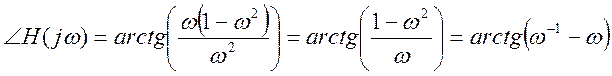
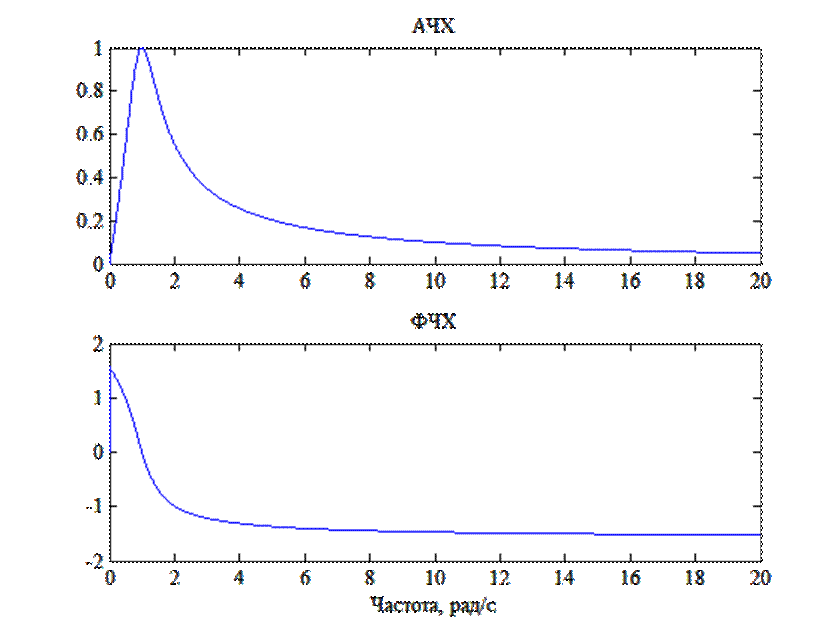
Рис. 8. Графики АЧХ и ФЧХ RLC – цепи.
Ответ. 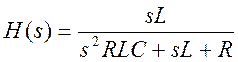
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.