Линейные непрерывные стационарные системы. Вариант 4

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Кафедра ССОД

Лабораторная работа № 7

«Линейные непрерывные стационарные системы»

Выполнил студент:

Факультет: АВТ

Группа: АИ-22

          Серебрянников В. Н.

Преподаватель:

Доц.  Щетинин Ю. И.

Новосибирск 2004г.

Цель работы:знакомство с динамическими характеристиками  линейных непрерывных стационарных (инвариантных во времени) систем  и их использованием для анализа систем в среде MATLAB.

1. Определение передаточной  функции активного фильтра (рис. 1).  При этом операционный усилитель предполагается идеальным с бесконечно большим коэффициентом усиления и бесконечным входным сопротивлением.

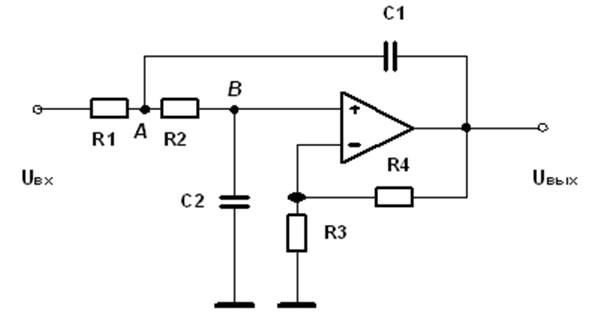
Рис. 1. Схема фильтра нижних частот

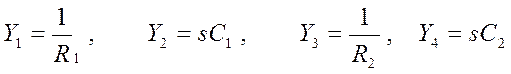
Первый закон Кирхгофа для узла  А:

.                                                   

Выразим токи через напряжения и проводимости Y_i

.                     

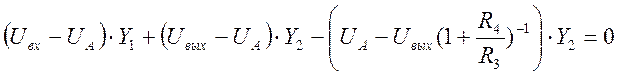Отсюда выражение для потенциала узла А

                         .                               

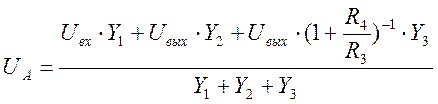Выражение для тока узла B

 .                     

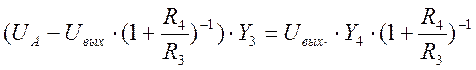Отсюда

                                                           .                                                

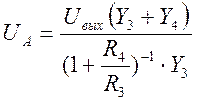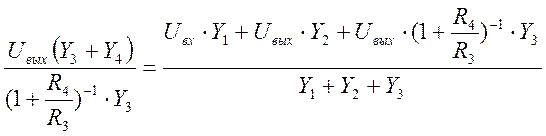
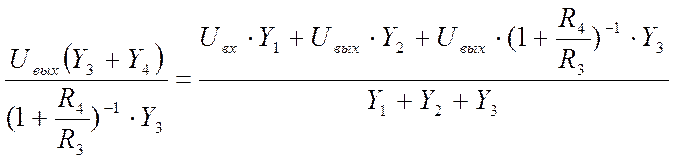
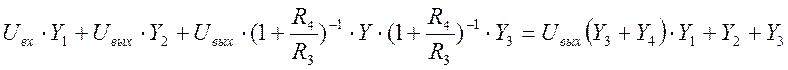
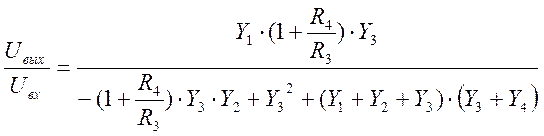
Передаточная функция  данного фильтра, как отношение преобразований Лапласа выходного и входного сигнала, имеет вид

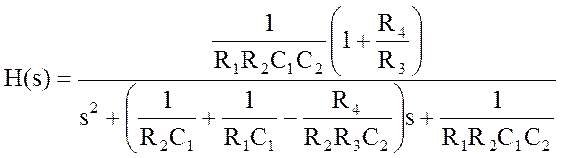
R1=1 кОм, R2=0,5 кОм, R3=2 кОм, R4=10 кОм,   С1=0,1 мкФ,    С2= 1  мкФ

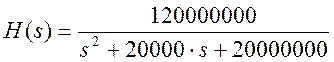
2. Определение нулей и полюсов фильтра с помощью функций  roots() и tf2zp().  

   Найдем нули и полюса фильтра с помощью функции roots():

>> den=[1 20000 20000000];

>> R=roots(den)

R =

  1.0e+004 *

   -1.8944

   -0.1056

Определим нули и полюса фильтра с помощью функцииtf2zp():   

>> den=[1 20000 20000000];

>> num=[120000000];

>> [z, p, k]=tf2zp(num, den)

z =

   Empty matrix: 0-by-1

p =

  1.0e+004 *

   -1.8944

   -0.1056

k =

   120000000

Построение диаграммы нулей и полюсов с помощью функции zplane(z,p).

>> zplane(z,p)

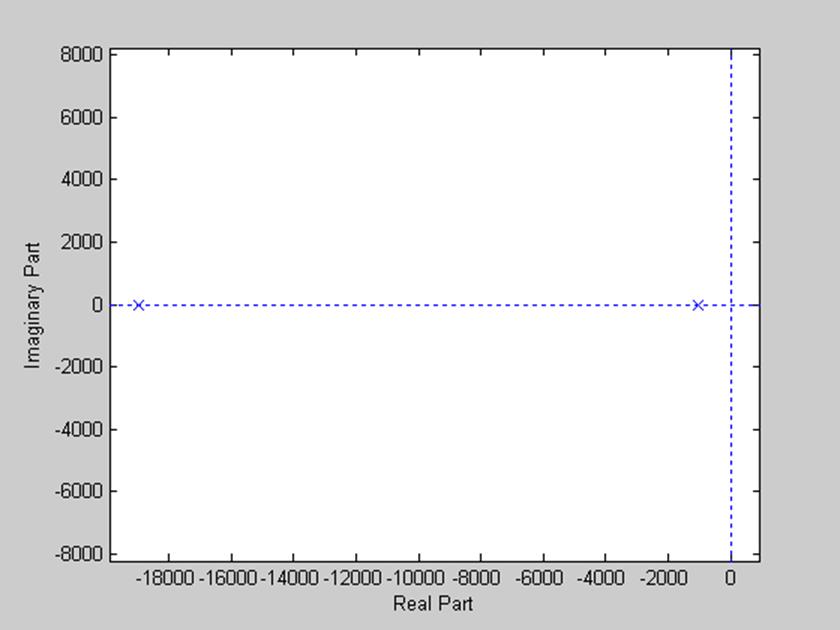
Рис. 2. Полюса фильтра

3. Разложение передаточной функции на простые (элементарные) дроби с использованием функции residue().

>>den=[1 20000000 20000000];

>>num=[120000000];

>> [z,p,k]=residue(num, den)

z =

  1.0e+003 *

   -6.7082

    6.7082

p =

  1.0e+004 *

   -1.8944

   -0.1056

k =

     []

4. Построение диаграммы Боде (функция bode()) .Определение частоты среза по уровню 3дБ и полосы пропускания фильтра.

>> num=[120000000];

>>den=[1 20000 20000000];

>>bode(num, den)

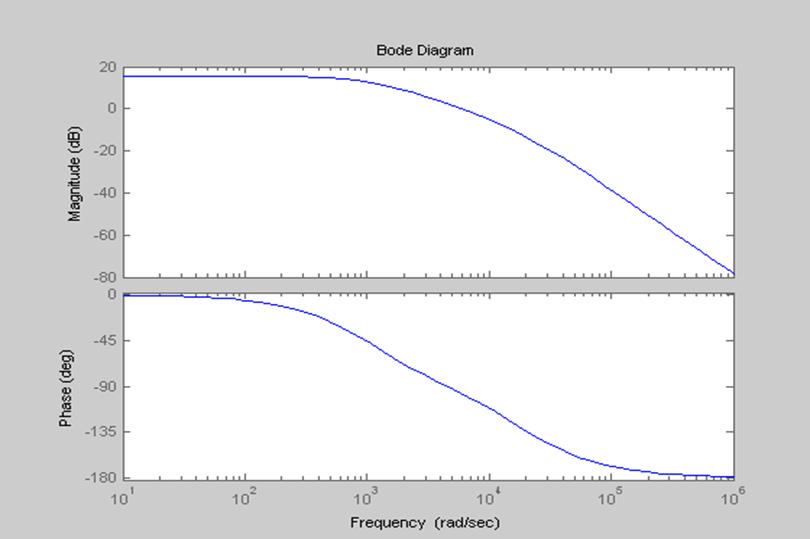
рис.3 Диаграмма Боде

Частота, на которой коэффициент передачи равен (спад коэффициента передачи равен 3 дб), называется частотой среза. Для данного фильтра частота среза приблизительно равна 1000 рад/сек.

Интервал частот, в пределах которых значение АЧХ уменьшается на, называется полосой пропускания системы. Полоса пропускания фильтра в пределах от нуля до 1000 рад/сек.

          Построение графиков АЧХ  и ФЧХ фильтра (функция freqs()).

>>num=[120000000];

>>den=[1 20000 20000000];

>>freqz(num,den)

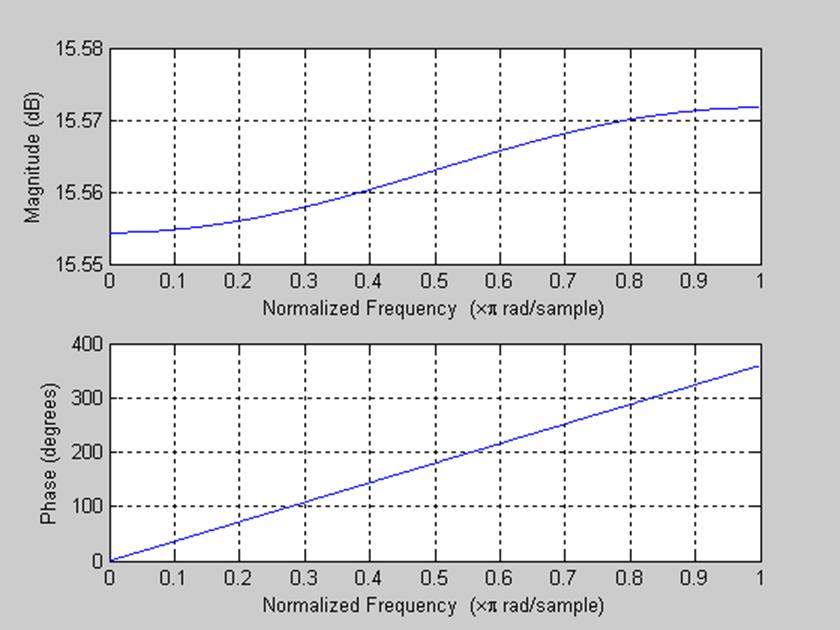
рис. 4 Графики АЧХ и ФЧХ системы.

5.ПостроениеАЧХ, ФЧХ и полосы пропускания фильтра при изменении значений параметров схемы. 

а) Для исследования поведения АЧХ И ФЧХ фильтра при изменении параметров схемы увеличим сопротивление резистора R₁=1кОм в 4 раза.

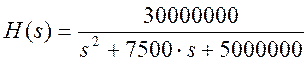
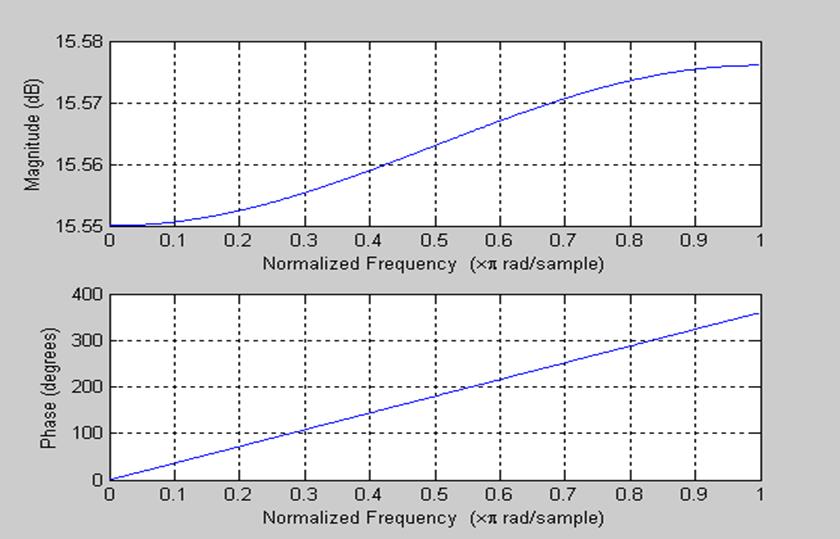
рис. 5 АЧХ и ФЧХ фильтра при R₁ = 4 кОм.

Частота среза при увеличении R₁ в 4 раза стала  примерно равна 650 рад/сек.

Соответственно полоса пропускания уменьшилась, т.е. интервал частот составляет промежуток от нуля до 650 рад/сек.

б) Уменьшим сопротивление резистора R₁ в 4 раза. Передаточная функция системы при этих изменениях примет вид:

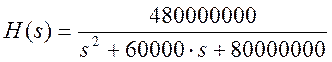
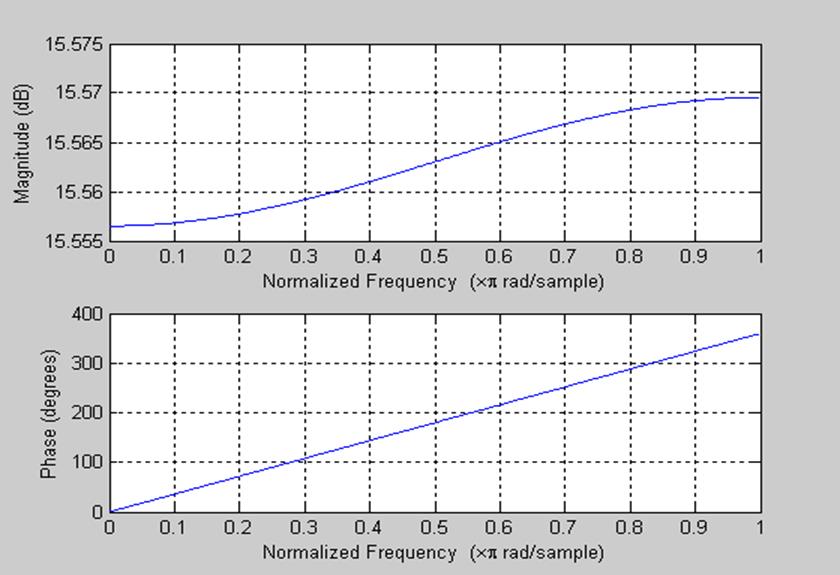
рис. 6 АЧХ и ФЧХ фильтра при R₁ = 250 Ом.

Частота среза при уменьшении R₁ в 4 раза стала  примерно равна 1350 рад/сек.

Соответственно, полоса пропускания уменьшилась вдвое, т.е. интервал частот  будет составлять промежуток от нуля до 1350 рад/сек.

Вывод:

6. Построение  графиков переходной и импульсной   характеристик фильтра с помощью функции step() и impulse().

>>num=[120000000];

>>den=[1 20000 2000000];

>>step(num, den)

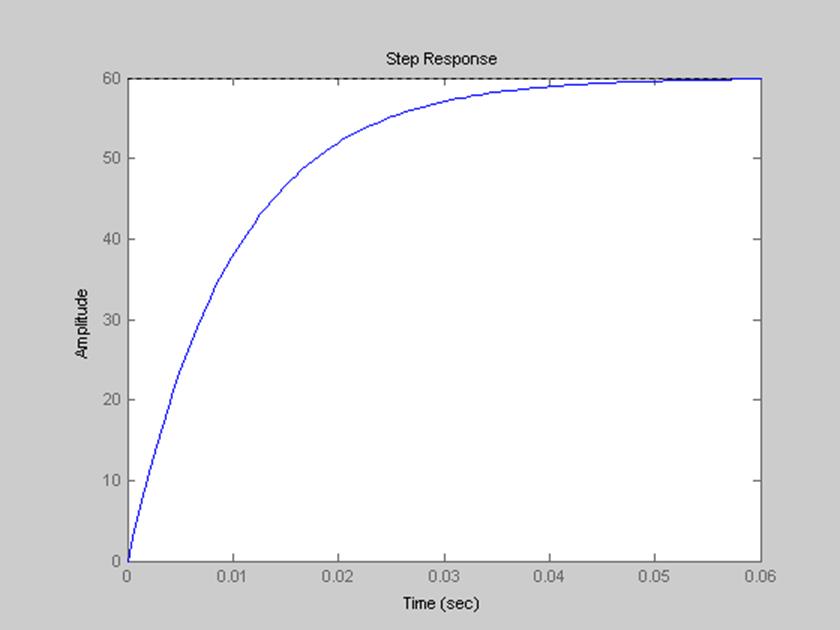
рис. 7 График переходной  характеристики фильтра

>>num=[120000000];

>>den=[1 20000 2000000];

>>impulse(num, den)

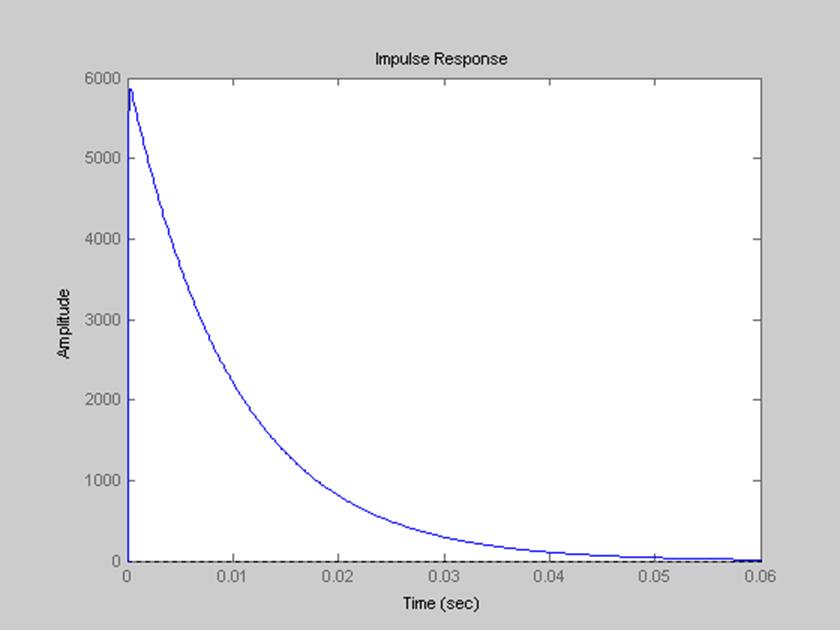
Рис. 9. График импульсной характеристики фильтра

Переходной называется функция, которая описывает реакцию ЛНСС на единичную ступенчатую функцию при нулевых начальных условиях. Обозначается как h(t).

            Импульсной называется функция, которая описывает реакцию ЛНСС на единичное импульсное воздействие при нулевых начальных условиях. Обозначается как g(t).

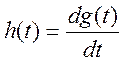- связь между переходной и импульсной характеристиками системы.

7. Определение входного гармонического сигнала с частотой, входящей в полосу пропускания фильтра. Нахождение отклика (выходного сигнала) системы на данный входной сигнал, с  использованием функции lsim(). Построение графиков входного и выходного сигналов.

М-файл:

n=[120000000];                     % Числитель и знаменатель передаточной функции

d=[1   20000    20000000];

 t= linspace(0,0.15,151);        % Задание временного интервала

 u=cos(2*pi*100*t);               % Входной сигнал

 [y,x]=lsim(n, d, u, t);            % Выходной сигнал

 plot(t,y,'r',t,u,'k');

 axis([0, 0.1, -6.5, 6.5])

 xlabel('Time,  sec'); 

 ylabel('Amplitude');

Реализация М-файла:

>>response

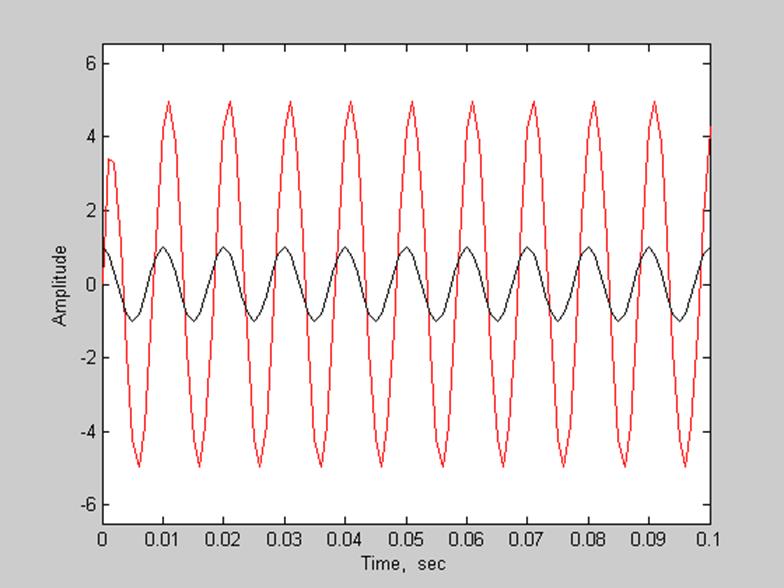
рис. 9 Графики входного и выходного сигналов.

Вывод: При подаче гармонического сигнала на вход системы с частотой 628 рад/сек. (выбранная частота входит в полосу пропускания фильтра) был найден отклик (выходной сигнал).

По  представленному графику видно, что амплитуда выходного сигнала приблизительно равна 5. Выходной сигнал «опережает» входной по фазе.

Если на вход мы подаем сигнал: , частота которого равна 628 рад/сек.

   Выходной сигнал (отклик) определяется как  .

 ,

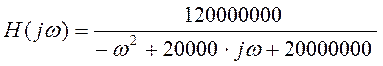
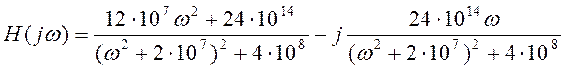
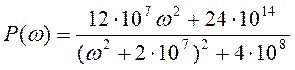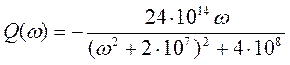
, при    

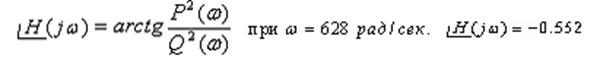
Из расчетов видно, что амплитуда выходного сигнала составляет 5.01 и фаза отклика составляет  .

Сопоставив экспериментально полученные данные с аналитическими расчетами, можно сделать вывод о том, что значительных расхождений между ними нет, т.е. аналитические расчеты подтверждают правильность экспериментального определения выходного сигнала на гармонический входной.