






НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов»
Лабораторная работа № 7
«Линейные непрерывные стационарные системы»
Группа: АИ-52
Студент: Повещенко А.А.
Вариант: 3
Преподаватель: доц. Щетинин Ю. И.
Новосибирск, 2007
Цель работы:
Знакомство с динамическими характеристиками линейных непрерывных стационарных (инвариантных во времени) систем и их использованием для анализа систем в среде MATLAB.
Схема фильтра
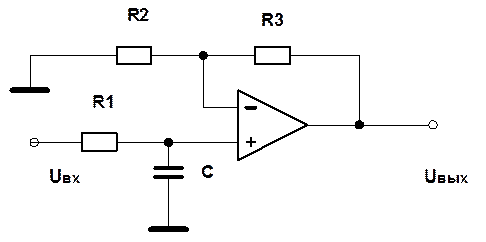
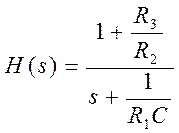
Рис.1. Фильтр низких частот.
R1=1 кОм,R2=1 кОм, R3=500 кОм, C=0,5 мкФ.
В силу предположения об идеальности предлагаемого ОУ считаем его входные токи нулевыми:
![]() .
.
Тогда, 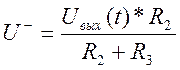
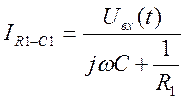
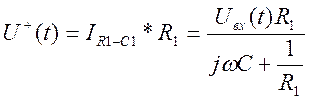
Для идеального операционного усилителя, охваченного отрицательной обратной связью
![]() . Отсюда,
. Отсюда,
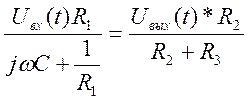
Поскольку передаточная функция линейной системы представляет собой отношение преобразований Лапласа выходного и входного сигналов при н.н.у., то выразим преобразование Лапласа от обеих частей полученного уравнения.
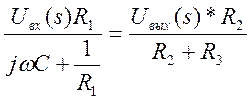
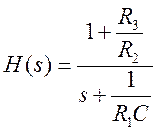
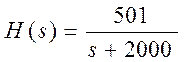
2. Определение полюсов и нулей передаточной функции.
Функция roots(C) вычисляет корни полинома с коэффициентами, указанными в векторе С. Общий вид полинома: C(1)*X^N + ... + C(N)*X + C(N+1).
>> num=[501];
>> den=[1 2000];
Определение нулей передаточной функции:
>> x=roots(num)
x = Empty matrix: 0-by-1
Определение полюсов передаточной функции:
>> y=roots(den)
y = -2000
Определение нулей, полюсов и коэффициента усиления с помощью функции tf2zp():
>> [z, p, k]=tf2zp(num, den)
z = Empty matrix: 0-by-1
p = -2000
k = 501
>> zplane(num, den)
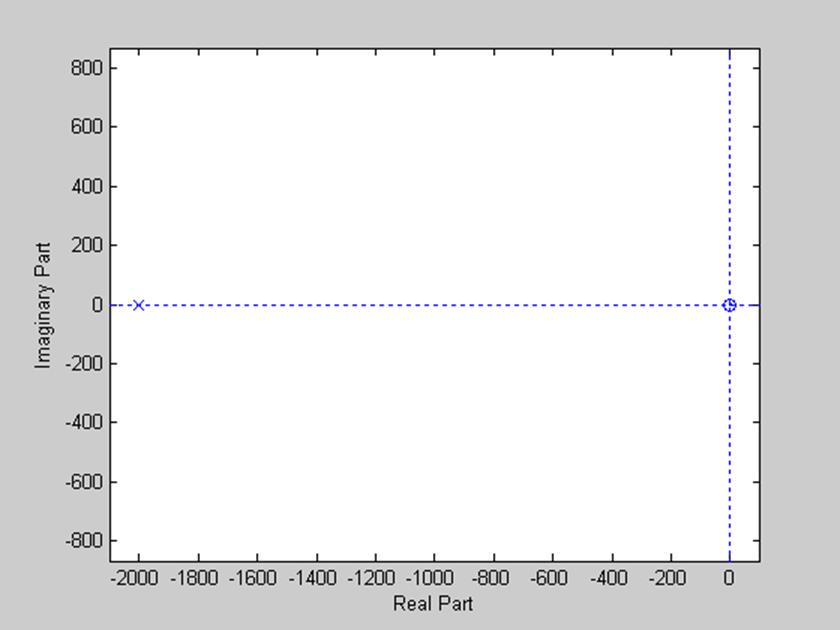
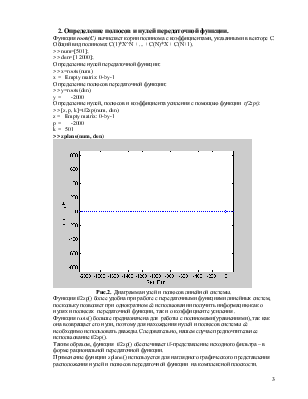
Рис.2. Диаграмма нулей и полюсов линейной системы.
Функция tf2zp() более удобна при работе с передаточными функциями линейных систем, поскольку позволяет при однократном её использовании получить информацию как о нулях и полюсах передаточной функции, так и о коэффициенте усиления .
Функция roots() больше предназначена для работы с полиномами(уравнениями), так как она возвращает его нули, поэтому для нахождения нулей и полюсов системы её необходимо использовать дважды. Следовательно, нашем случае предпочтительнее использование tf2zp().
Таким образом, функция tf2zp() обеспечивает tf-представление исходного фильтра – в форме рациональной передаточной функции.
Применение функции zplane()
используется для наглядного графического представления расположения нулей и
полюсов передаточной функции на комплексной плоскости. Рассматривая положения
полюсов передаточной функции системы мы можем судить об устойчивости системы в
целом, а также проводить оценку качества переходных процессов в системе. Необходимым
и достаточным условием устойчивости системы является расположение
всех полюсов ПФ в левой полуплоскости - ![]() .
Следовательно, наша система будет устойчивой.
.
Следовательно, наша система будет устойчивой.
3. Разложение передаточной функции на простые (элементарные) дроби.
>> [z1 p1 k1]=residue(num, den)
z1 = 501
p1 = -2000
k1 = []
Т.к. степень полинома знаменателя больше, чем степень полинома числителя, то целая часть их отношения равна 0, поэтому k = [] (пустая матрица).
Функция residue() осуществляет разложение непрерывной передаточной функции на простые дроби
следующим образом.
B(s) R(1) R(2) R(n)
H(s) = ---- = -------- + -------- + ... + -------- + K(s)
A(s) s - P(1) s - P(2) s - P(n)
В этой форме представления передаточная функция описывается:
· вектором – столбцом R вычетов передаточной функции
· вектором – столбцом P полюсов передаточной функции
· вектором – строкой К коэффициентов целой части дробно – рациональной функции.
Тогда H(s)=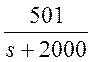
Функция residue() позволяет представить передаточную функцию в виде её разложения на простые дроби с выделением целой части. Кроме того, с помощью данной функции можно осуществить и обратное преобразование(переход): от разложения к передаточной функции.
4. Построение диаграммы Боде (функция bode()) и графиков АЧХ и ФЧХ фильтра (функция freqs()). Нахождение частоты (частот) среза по уровню 3дБ и полосы пропускания фильтра.
num=[501];
den=[1 2000];
bode(num, den)
figure(2)
w=0:10:1000;
freqs(num,den,w)
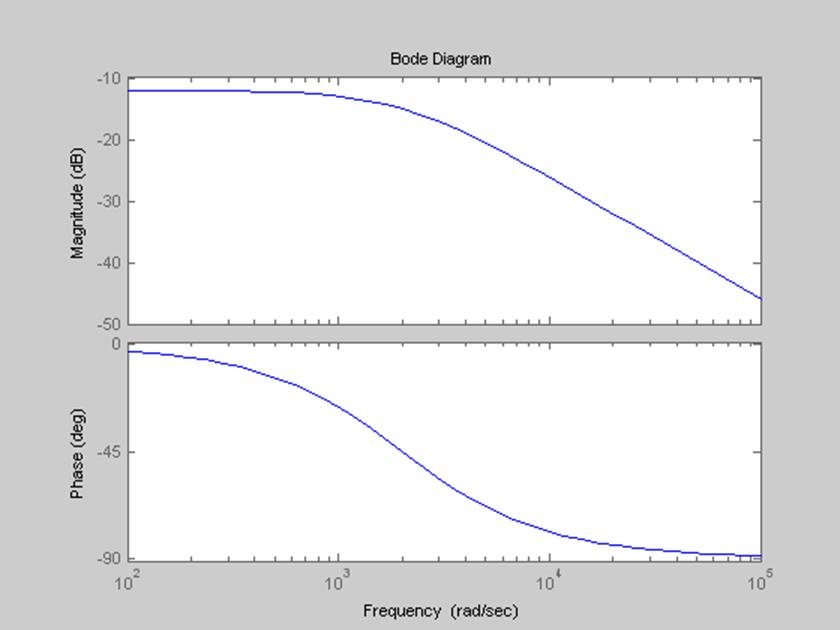
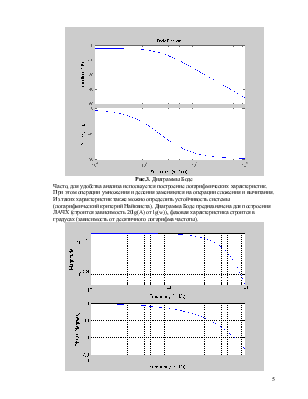
Рис.3. Диаграммы Боде
Часто, для удобства анализа используется построение логарифмических характеристик. При этом операции умножения и деления заменяются на операции сложения и вычитания. Из таких характеристик также можно определить устойчивость системы (логарифмический критерий Найквиста). Диаграмма Боде предназначена для построения ЛАЧХ (строится зависимость 20lg(A) от lg(w)), фазовая характеристика строится в градусах (зависимость от десятичного логарифма частоты).
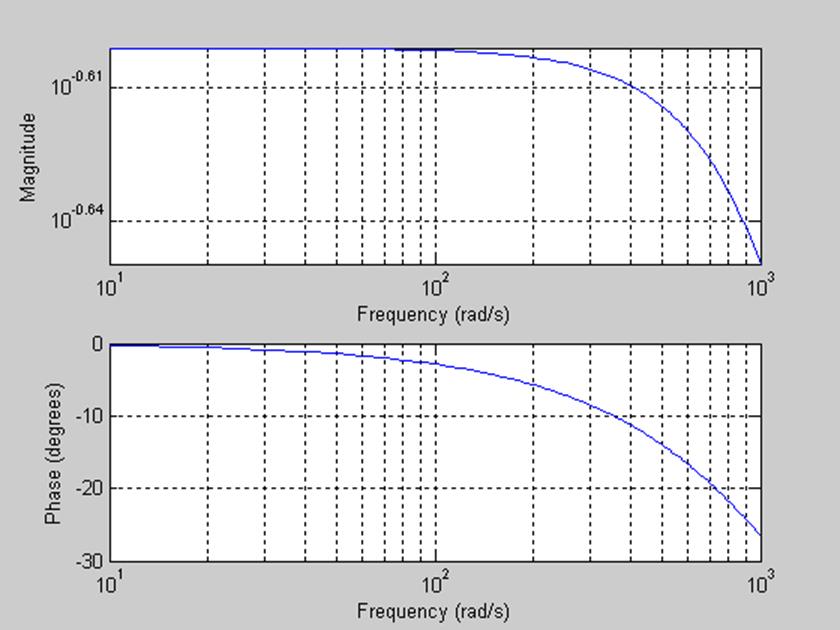
Рис.4. АЧХ и ФЧХ системы.
Модуль передаточной функции 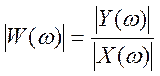 является
АЧХ и характеризует изменение амплитуды гармонического сигнала при прохождении
его через систему. Аргумент
является
АЧХ и характеризует изменение амплитуды гармонического сигнала при прохождении
его через систему. Аргумент 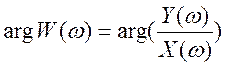 представляет
собой ФЧХ системы, показывающую изменение фазы гармоники на выходе системы.
представляет
собой ФЧХ системы, показывающую изменение фазы гармоники на выходе системы.
Исходя из диаграммы Боде (или АЧХ фильтра), частота, при котором отклонение амплитуды не превышает 3 дБ от максимального значения. Таким образом, полоса пропускания фильтра составляет промежуток (10,103).
5. Поиск полосы пропускания фильтра при изменении параметров схемы.
a)R1=2 кОм;
R2=1 кОм;
R3=500 кОм;
C=0,5 мкФ.
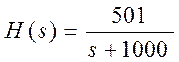
б)R1=20 кОм;
R2=1 кОм;
R3=500 кОм;
C=0,5 мкФ.
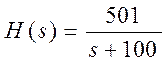
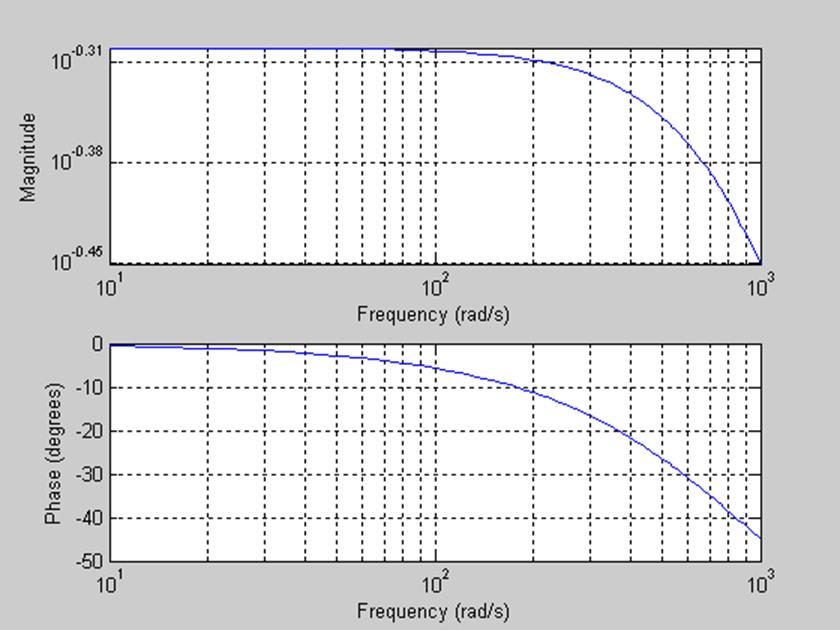
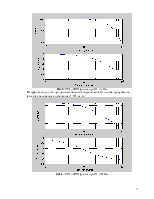
Рис.5.АЧХ и ФЧХ фильта при R1=2 кОм.
Из графика видно, что при данном значении сопротивления R1 полоса пропускания фильтра стала меньше и составила (1,102) рад/с.
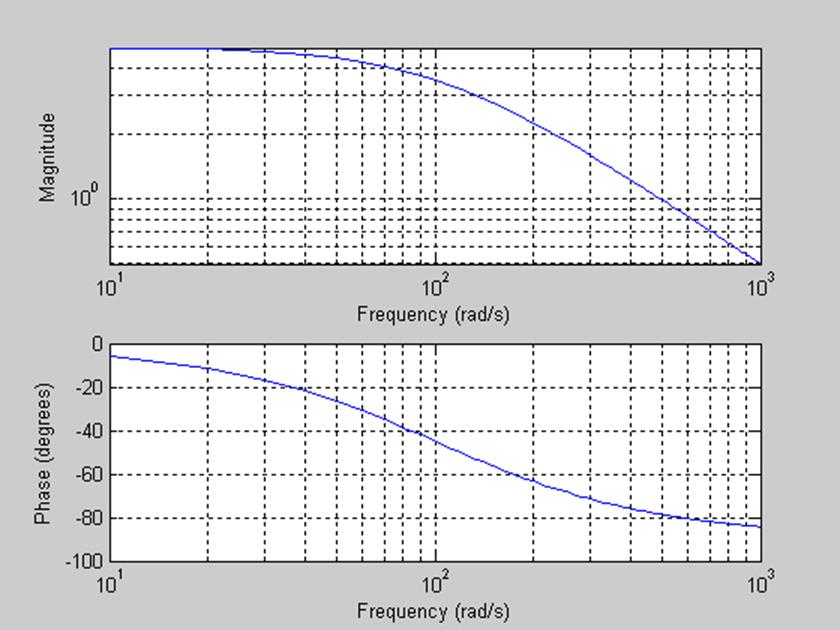
Рис.6. АЧХ и ФЧХ фильта при R1=20кОм.
Из графика видно, что при данном значении сопротивления R1 полоса пропускания фильтра стала больше и составила (1,103) рад/с.
6. Построение переходной и импульсной характеристик фильтра.
Переходной характеристикой называют отклик системы на входное воздействие в виде единичной ступенчатой функции при нулевых начальных условиях.

Рис.7. Структурная схема получения переходной функции.
Импульсная характеристика – реакция системы на входной сигнал в виде дельта-функции при нулевых начальных условиях.
Импульсная переходная функция является производной переходной функции звена:
Рис.8. Структурная схема получения импульсной характеристики.
num= 501;
den= [1 2000];
figure(1)
impulse(num, den);
figure(2)
step(num, den)
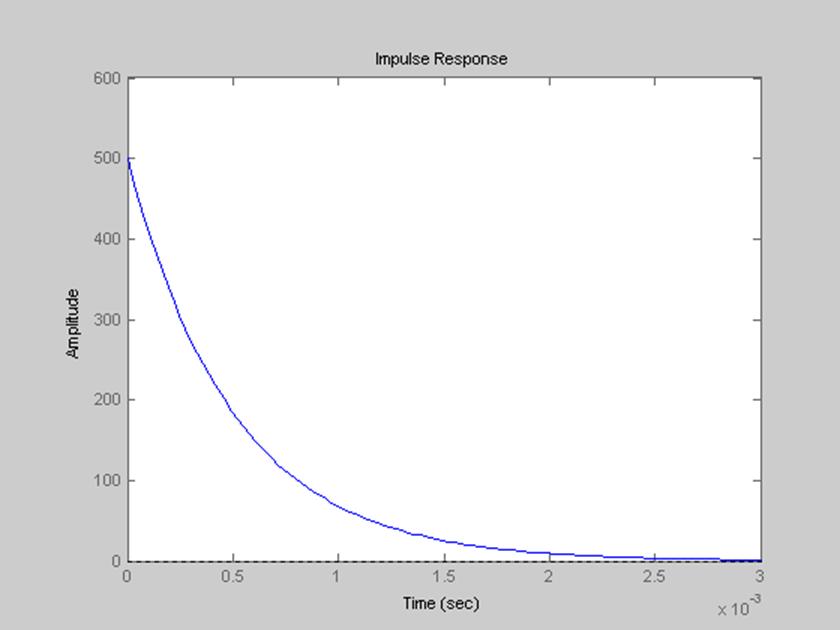
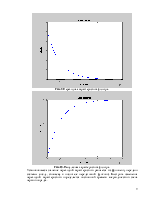
Рис.9. Переходная характеристика фильтра.
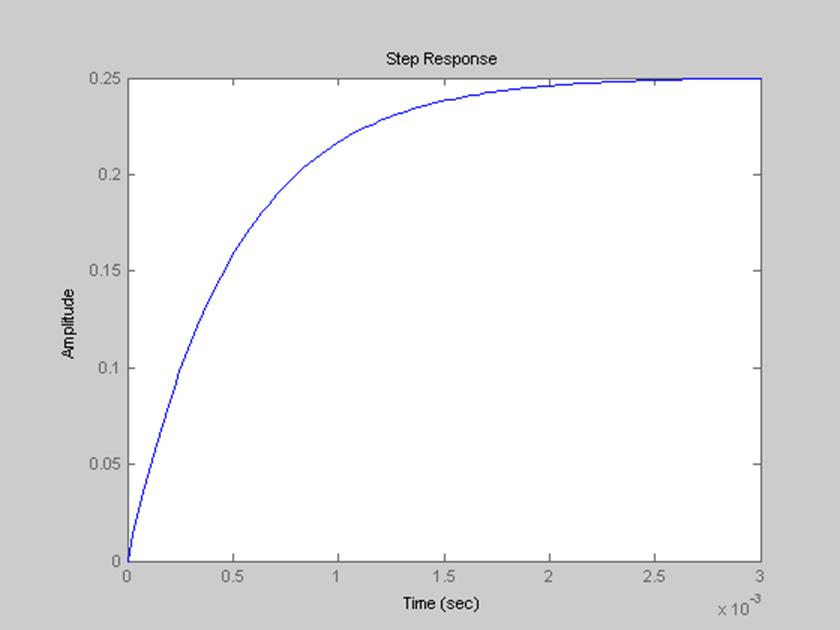
Рис.10. Импульсная характеристика фильтра.
Установившееся значение переходной характеристики равняется коэффициенту передачи системы (числу, стоящему в числителе передаточной функции). Быстрота изменения переходной характеристики определяется постоянной времени апериодического звена первого порядка.
7. Оценка работы системы при подаче на вход гармонического сигнала с частотой, входящую в полосу пропускания фильтра.
n=[501]; % Числитель и знаменатель передаточной функции
d=[1 2000];
t= linspace(0,0.05,500); % Задание временного интервала
u=cos(2*pi*100*t); % Входной сигнал
[y,x]=lsim(n, d, u, t); % Выходной сигнал
plot(t,y,'r',t,u,'k');
axis([0, 0.05, -6.5, 6.5])
xlabel('Time, sec');
ylabel('Amplitude');
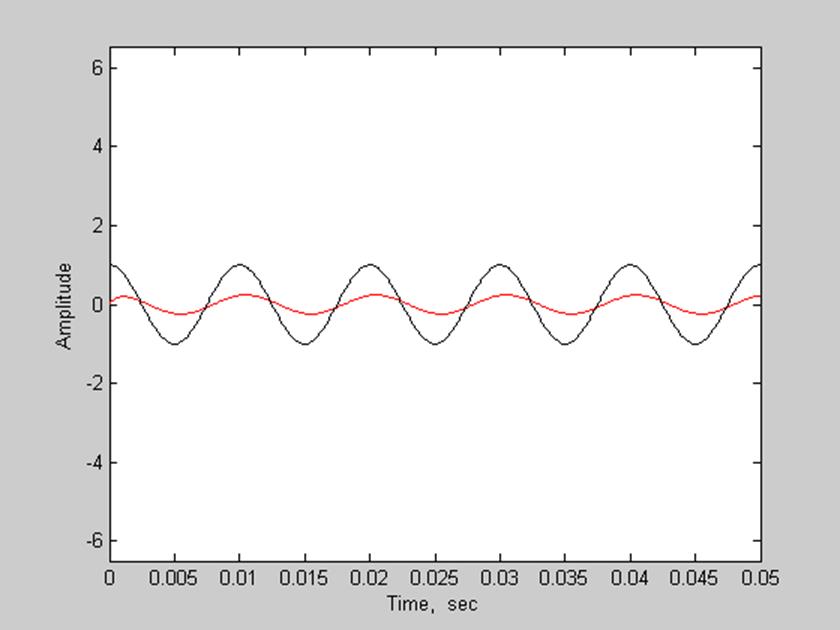
Рис.11. Графики сигнала, поданного на вход и сигнала, полученного с выхода фильтра.
Частота входного сигнала относится к тому диапазону частот, при которых не наблюдается отклонения амплитуды от максимального значения. Таким образом, на выходе фильтра получаем сигнал усиленный в k раз (k=501 – коэффициент передачи системы). Также происходит сдвиг по фазе.
7) Определение входного гармонического сигнала с частотой, входящей в полосу пропускания фильтра. Нахождение отклика (выходной сигнал) системы на данный входной сигнал. Построение графиков входного и выходного сигналов. Сделать аналитическую оценку выходного сигнала, базируясь на частотной характеристике системы и выражении для выходного сигнала в частотной области. Сопоставить результаты.
Для нахождения отклика (выходной сигнал) системы на данный входной сигнал использовать функцию lsim().
Вывод.
Линейные непрерывные стационарные системы – системы непрерывного времени, для которых справедлив принцип суперпозиции и задержке входного сигнала соответствует аналогичная задержка выходного сигнала. Эти системы описываются линейными однородными дифференциальными уравнениями с постоянными коэффициентамиЛинейные системы в зависимости от конкретной задачи, могут быть представлены в нескольких эквивалентных формах:
· в форме рациональной передаточной функции(в Matlab – tf-представление), являющейся отношением преобразований Лапласа выходного и входного сигналов при н.н.у.(п.1-2)
· в виде разложения передаточной функции на простые дроби. В этой форме динамическая система описывается тремя векторами: вектор-столбец вычетов ПФ, вектор-столбец полюсов и вектор-строка целой части дробно-рациональной функции.(п.3)
· имеется еще несколько форм представления линейных систем.
Например, в п.2 при построении графика расположения нулей и полюсов системы использовалось tf-представление . Информация о корнях ХП системы позволяет судить об её устойчивости.
Основными характеристиками системы в частотной области являются АЧХ и ФЧХ, а также логарифмические частотные характеристики, которые , как правило, более удобны при анализе линейных систем. В Matlab имеется несколько функций, позволяющие получить информацию о линейной системе, представленной в определенной форме и построить её частотные характеристики. В данной работе для этой цели использовались bode(), freqs().
Основными временными характеристиками являются – импульсная и переходная, отражающие
реакцию системы на типовые входные сигналы: дельта – функцию и ступенчатую, которые используются для исследования поведения линейных систем во время переходного процесса.
В Matlab имеется несколько функций, позволяющие получить данные характеристики. Нами использовались две: impulse() и step(), которые осуществляют построение их графиков.
Важным понятием линейных систем является обратная связь, отражающая ситуацию, когда часть выходного сигнала, в зависимости от коэффициента ОС подаётся на вход системы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.