НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов», 5-й семестр
ЛАБОРАТОРНАЯ РАБОТА № 7.
ЛИНЕЙНЫЕ НЕПРЕРЫВНЫЕ
СТАЦИОНАРНЫЕ СИСТЕМЫ
Цель работы:знакомство с динамическими характеристиками линейных непрерывных стационарных (инвариантных во времени) систем и их использованием для анализа систем в среде MATLAB.
Задание и порядок выполнения работы.
1. Определите передаточную функцию активного фильтра (вариант – по индивидуальному заданию, приложение 1). Схему фильтра и процедуру получения его передаточной функции поместите в отчет. При этом операционный усилитель предполагается идеальным с бесконечно большим коэффициентом усиления и бесконечным входным сопротивлением. Соответствующий пример см. в приложении 2.
2.
Запишите векторы коэффициентов полиномов
числителя и знаменателя передаточной функции фильтра. С помощью функции roots() найдите нули и полюса фильтра.
Получите также нули, полюса и коэффициент усиления фильтра с помощью функции
tf2zp().
Постройте диаграмму нулей и полюсов, используя функцию zplane(z,p).
Запишите передаточную функцию фильтра через полюсы и нули и сопоставьте её с
исходной.
3. Выполните разложение передаточной функции на простые (элементарные) дроби с использованием функции residue(). Запишите это разложение, используя выходные аргументы residue(). Сопоставьте полученное выражение с выражением передаточной функции из п.1.
4.
Постройте графики АЧХ и ФЧХ
фильтра с помощью функции freqs(). Используйте для этого синтаксис [h,w] = freqs(b,a). Найдите
частоту среза фильтра по уровню 3дБ и полосу пропускания фильтра.
Постройте также диаграмму Боде (функция bode()). Поясните особенности этой диаграммы.
5. Изменяя значения параметров схемы (резисторов и конденсаторов), пронаблюдайте и прокомментируйте изменение АЧХ, ФЧХ и полосы пропускания фильтра для двух – трех характерных сочетаний значений параметров.
6. С помощью функций step() и impulse() постройте
графики переходной и импульсной характеристик фильтра.
Покажите связь импульсной характеристики и передаточной функции системы.
Используя разложение передаточной функции из п.3, найдите аналитически
импульсную характеристику фильтра. Постройте её график. Сопоставьте
результаты.
7. Определите входной гармонический сигнал с частотой,
входящей в полосу пропускания фильтра. Используя функцию lsim(), найдите отклик (выходной
сигнал) системы на данный входной сигнал. Постройте графики входного и
выходного сигналов.
Сделайте аналитическую оценку выходного сигнала, базируясь на частотной
характеристике системы и выражении для выходного сигнала линейной системы при
гармоническом входном сигнале. Постройте график. Сопоставьте результаты.
8.
Сделайте необходимые пояснения,
заключения и выводы с учетом цели работы, окончательно оформите отчет по
лабораторной работе.
В отчете должны быть представлены:
§ титульный лист,
§ название и цель работы,
§
формулировки пунктов работы,
команды и .m – файлы,
комментарии, выводы.
9. Проверьте свою подготовленность по контрольным вопросам. Защитите лабораторную работу.
ЛИТЕРАТУРА.
1. Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов.: Уч. Пособие.- Новосибирск. Изд-во НГТУ, 1998 - ч.2, стр. 5 – 26.
2. Голышев Н.В., Щетинин Ю.И. Задачник-практикум по теории и обработке сигналов.: Уч. пособие.- Новосибирск. Изд-во НГТУ, 2001, стр. 41 – 52.
3. Сергиенко А.Б. Цифровая обработка сигналов. - СПб.: Питер, 2003, стр. 87- 90,
93 - 96.
Web-ресурсы:
1. http://tiger.cs.nstu.ru/Tos/zerpol/start.html
2. http://tiger.cs.nstu.ru/Tos/filter/start.html
3. http://www.jhu.edu/~signals/explore/index.html
Контрольные вопросы и упражнения.
1. Сформулируйте принцип суперпозиции и поясните его физический смысл. Как используется этот принцип в анализе линейных систем?
2. Приведите определение импульсной характеристики линейной непрерывной системы (ЛНС). Как можно экспериментально измерить импульсную характеристику?
3. Запишите и объясните выражение и вычисление интеграла свертки.
4. Пусть входной сигнал x(t) и импульсная характеристика w(t) ЛНС имеют вид
 |
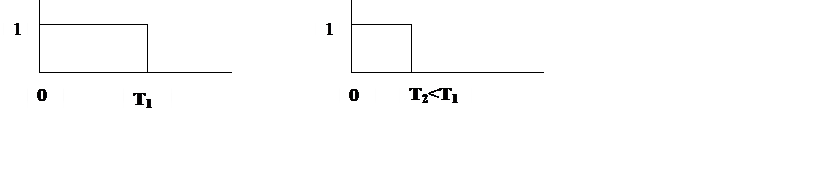Рис.1.
Основываясь на геометрическом смысле свертки, изобразите вид выходного сигнала.
5. Система имеет переходную характеристику вида
.
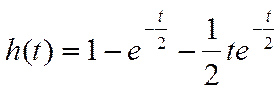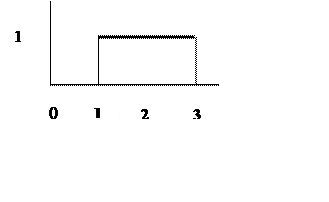На вход системы подается сигнал вида
 |
Рис.2.
Выразите входной сигнал в виде разности единичных ступенчатых функций и согласно принципу суперпозиции представьте выходной сигнал как разность откликов системы на каждый из ступенчатых сигналов.
6. Сформулируйте определение передаточной функции ЛНС. Какими преимуществами обладает передаточная функция при анализе линейных систем? Как представляется передаточная функция в Matlab?
7. Как вычисляются импульсная и переходная характеристики в системе Matlab?
8.
Как определяется АЧХ системы по
её уравнению? Экспериментально?
Объясните физический смысл АЧХ и ФЧХ системы.
9. Как вычисляются и строятся графики АЧХ и ФЧХ в Matlab?
10. Что такое полоса пропускания системы? Поясните связь полосы пропускания с параметрами для пассивного RC-фильтра первого порядка.
11. Поясните соответствия (связи) между передаточной функцией, импульсной и переходной характеристиками, частотной характеристикой линейной непрерывной системы.
12. Определите передаточную функцию, полюса, АЧХ и ФЧХ RLC – цепи, изображенной на рис.
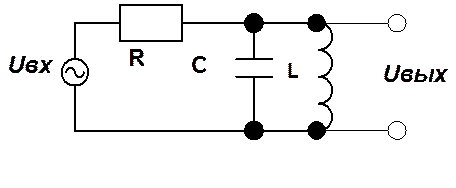
Рис.3.
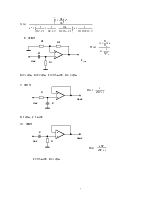
13. Передаточная функция системы имеет вид
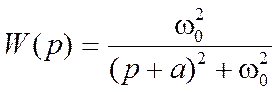
Найдите выражение для АЧХ системы. Как зависит её поведение от параметров a и ω0 ?
14. Что такое полюсы и нули передаточной функции системы? Как их расположение на комплексной плоскости влияет на поведение фильтра? Как по карте нулей и полюсов представить эскиз частотной характеристики системы?
15. Для фильтра верхних частот передаточная функция имеет вид
.
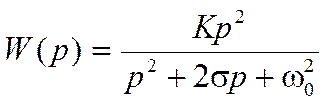Постройте
диаграмму полюсов и нулей. Проанализируйте поведение фильтра при изменении
положения полюсов и частоты 
.
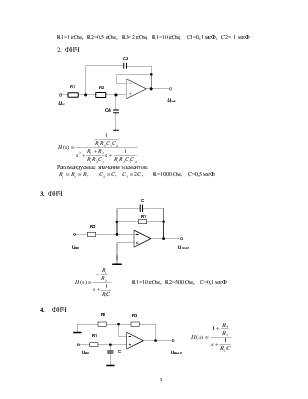
Приложение 1. Схемы фильтров для индивидуальных заданий.
1.
ФНЧ
,
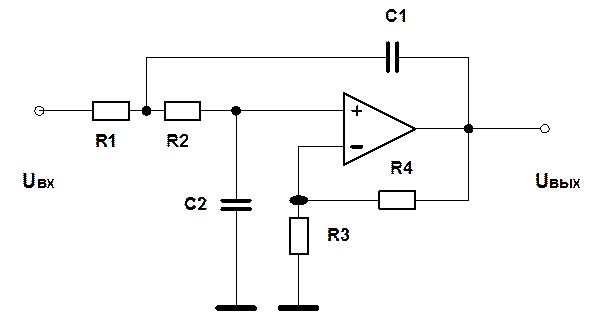
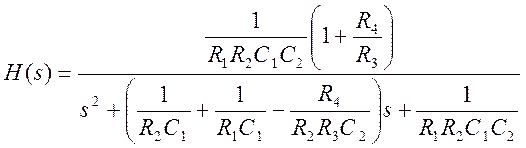Рекомендуемые значения элементов:
R1=1 кОм, R2=0,5 кОм, R3=2 кОм, R1=10 кОм, С1=0,1 мкФ, С2= 1 мкФ
2. ФНЧ
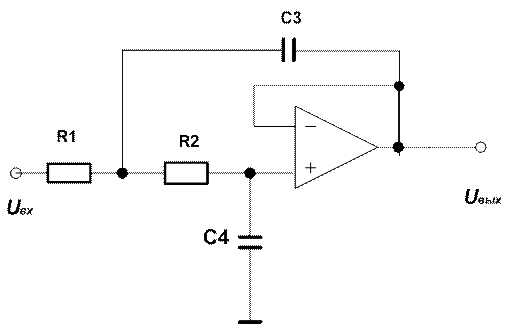
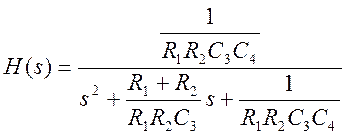
Рекомендуемые значения элементов:
, R=1000 Ом, С=0,5 мкФ.
3. ФНЧ
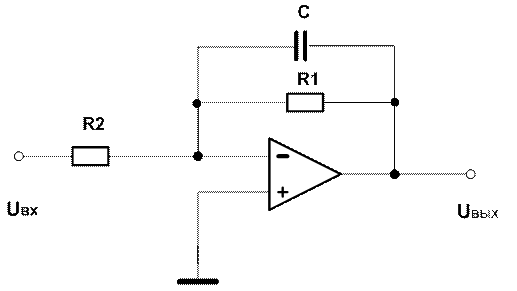
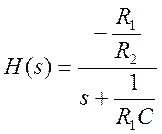R1=10 кОм, R2=500
Ом, C=0,1 мкФ
4. ФНЧ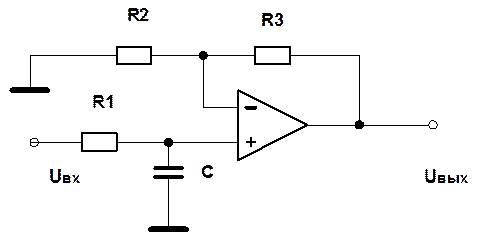 
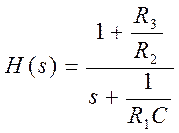
R1=1 кОм, R2=1 кОм, R3=500 кОм, C=0,5 кОм
5.
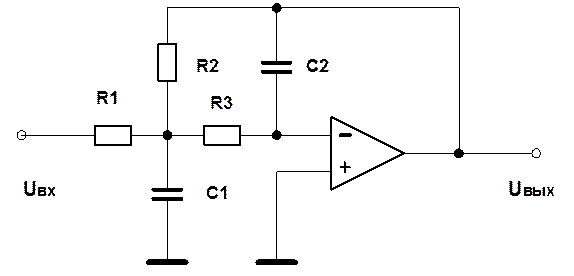ФНЧ
6.
7.
8.
9.
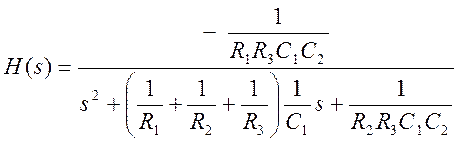
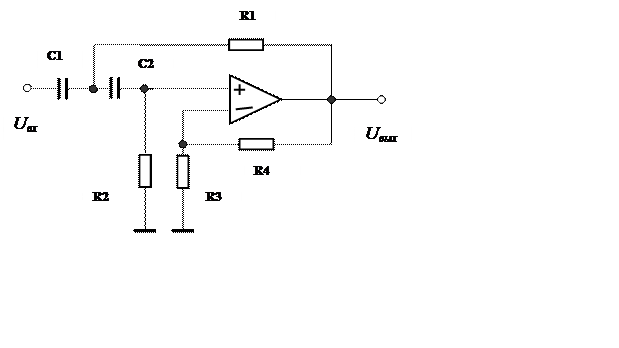
Рекомендуемые значения элементов:
R1=2 кОм, R2=40 кОм, R3=2
кОм,
C1=1 мкФ, C2=0,1 мкФ.
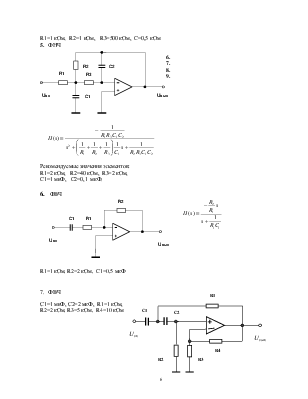
6.
ФВЧ
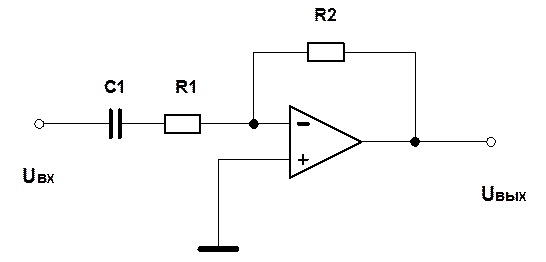
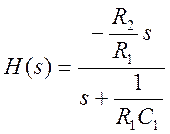
R1=1 кОм, R2=2 кОм, C1=0,5 мкФ
7.
ФВЧ
С1=1 мкФ, С2=2 мкФ, R1=1 кОм,
R2=2 кОм, R3=5 кОм, R4=10
кОм
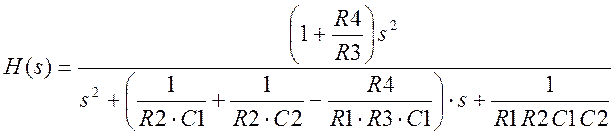
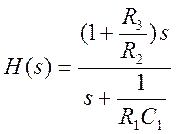
Uвых
R1=1 кОм, R2=2 кОм, C1=0,5 мкФ, R3=5 кОм
9. ФНЧ
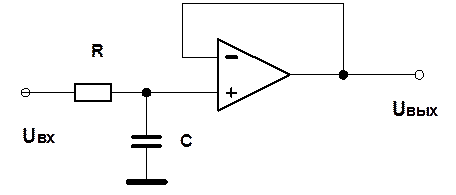
R=1кОм, С=1 мкФ
10. ФВЧ
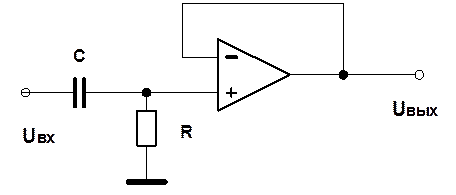
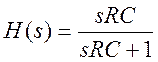
C=0,5 мкФ, R=1 кОм
11.
ПФ
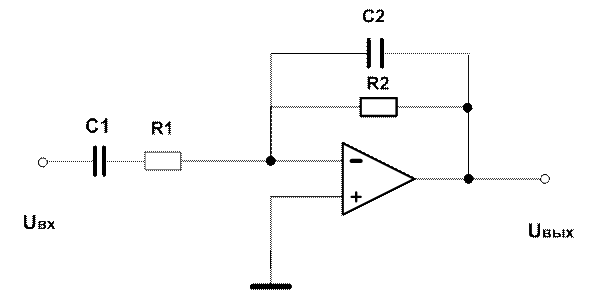
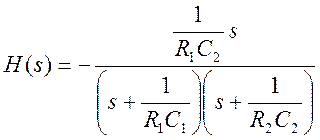
R1=10 кОм, C1=1 мкФ, R2=100 Ом, С2=10 мкФ.
12.
ПФ
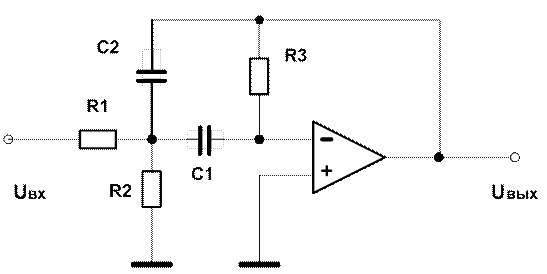
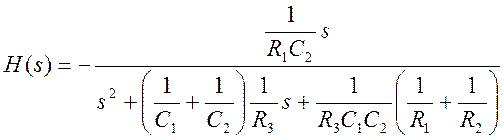
Рекомендуемые значения элементов:
С1=10 мкФ, С2=5 мкФ, R1=1 кОм, R2=1 кОм, R3=10 кОм.
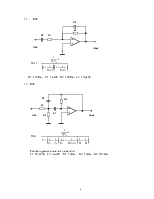
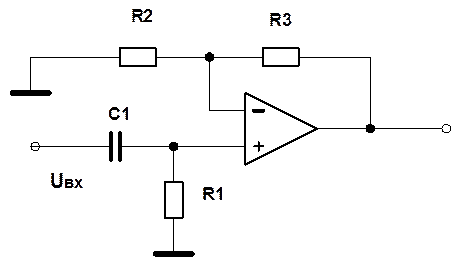
Приложение 2. Пример определения передаточной функции активного фильтра.
Будем предполагать, что операционный усилитель – идеальный, с бесконечно большим коэффициентом усиления без обратной связи и бесконечно большим входным сопротивлением. Поэтому Uвых = UB.
Схема фильтра
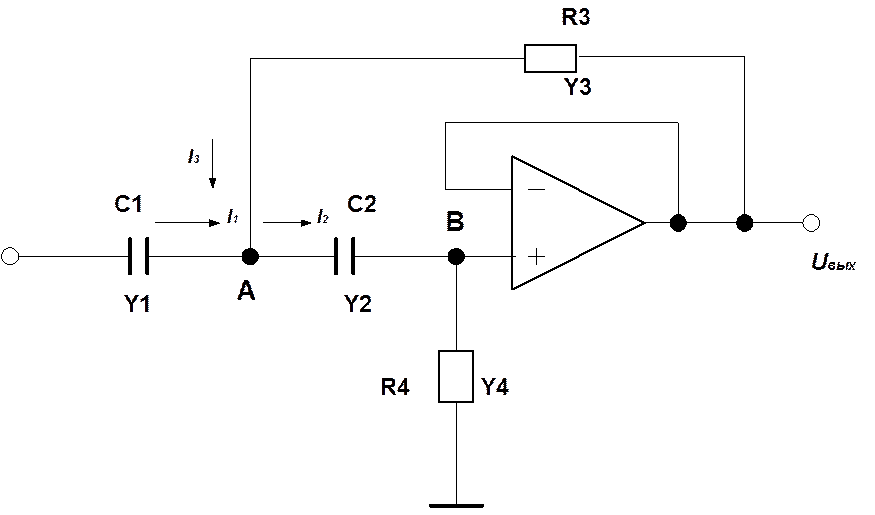
Рис.4.
Первый закон Киргофа для узла А:
. (1)
Выразим токи через напряжения и проводимости Yi
. (2)
Отсюда выражение для потенциала узла А
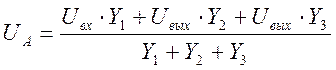. (3)
Выражение для тока узла B
. (4)
Отсюда
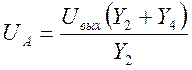. (5)
Подставляя (5) в (3), приводя подобные члены и составляя отношение выходного напряжения к входному, получаем
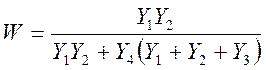(6)
Для рассматриваемого фильтра
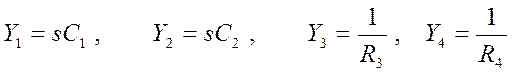. (7)
Передаточная функция данного фильтра, как отношение преобразований Лапласа выходного и входного сигнала, имеет вид
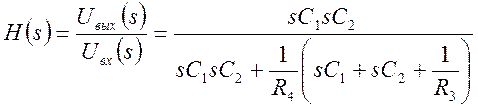. (8)
После упрощения (8) получим
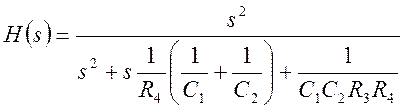. (9)
Если
в таком фильтре выбрать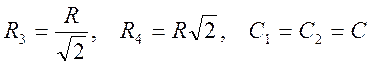 
, то он
будет представлять собой активный фильтр верхних частот Баттерворта с частотой
среза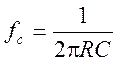 
.
Частота среза – это частота, при которой амплитудная частотная характеристика (АЧХ) снижается до уровня 1/√2 (в децибелах – на 3 дБ) от максимального значения
Ниже приведены амплитудно - частотная и фазовая частотная характеристика такого фильтра при С = 0,5 мкф и R = 500 Ом.
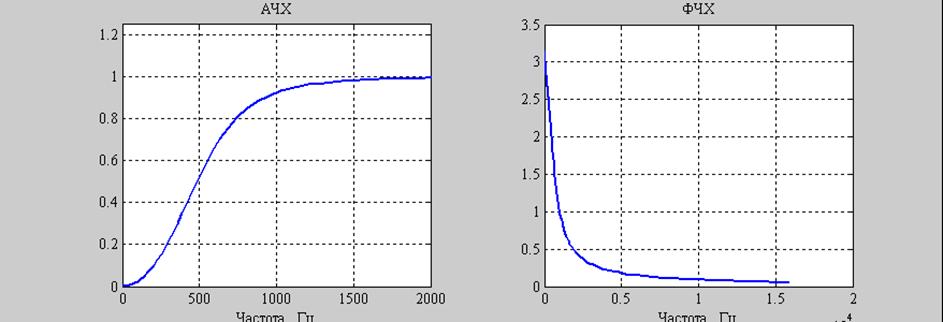
Рис.5.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.