






НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов», 6 - й семестр
ЛАБОРАТОРНАЯ РАБОТА № 8
Z - преобразование
и дискретно – временное преобразование Фурье
Выполнила: Ездакова Е.А. Преподаватель: Щетинин Ю.И.
Группа: АТ-53
Вариант: №7
Новосибирск, 2008
Цель работы:Изучение Z – преобразования и дискретно – временного преобразования Фурье (ДВПФ), их вычисления в среде Matlab.
Порядок выполнения работы:
1.
Выражения прямого и обратного Z - преобразования.
Нахождение аналитически Z – преобразование сигналов и их областей сходимости :
а) x[n] = δ[n],
б) x[n] = u[n],
в) x[n] = cos ωn.
Прямое и обратное Z – преобразования:
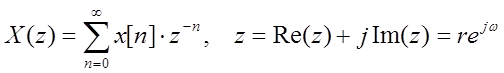 (0дностороннее)
(0дностороннее)
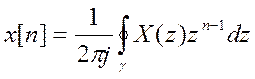
а) Z – преобразование сигнала x[n] = δ[n]:
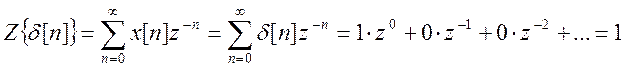
Область сходимости вся z-плоскость.
б) Z – преобразование сигнала x[n]
= u[n]:
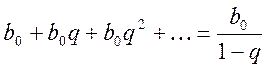 .
.
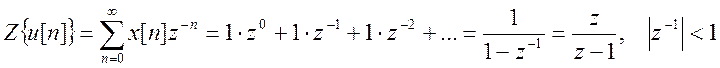 .
.
Полюс ![]() -
точка
-
точка ![]() .
.
Область сходимости: ![]() - внешность окружности единичного
радиуса.
- внешность окружности единичного
радиуса.
в)Z –
преобразование сигнала ![]() :
:
По
формуле Эйлера: 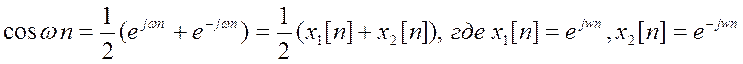
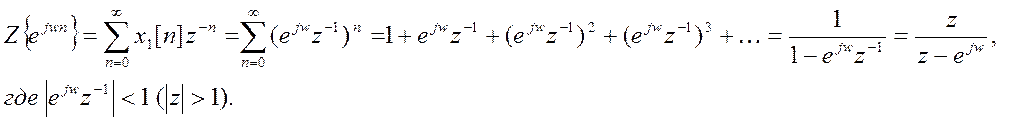
Аналогично:
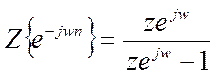 ,где (
,где (![]() ).
).
По свойству линейности Z-преобразования ![]() :
:
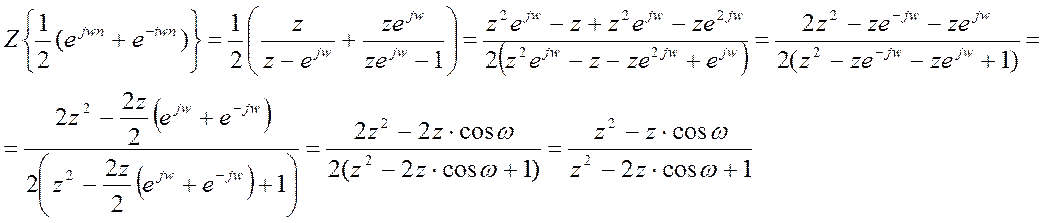
Область сходимости: ![]() - внешность окружности единичного
радиуса.
- внешность окружности единичного
радиуса.
3. Нахождение с помощью функции ztrans() Matlab Z – преобразования сигналов (последовательностей), их запись в обычной математической форме:
а) x[n] = an cos
ωn,
б) x[n] = n2 e2n,
в) x[n]
= cos2n.
а) Z-преобразование
последовательности ![]() :
:
symsawn
X=ztrans(a.^n*cos(w*n))
X =(z/a-cos(w))*z/a/(z^2/a^2-2*z/a*cos(w)+1)
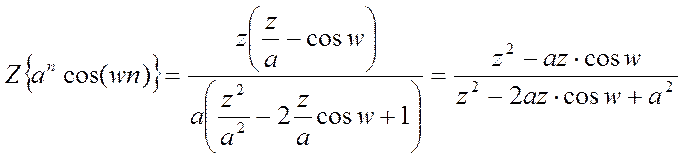
б) Z-преобразование
последовательности ![]() :
:
syms n
y=ztrans(n.^2*exp(2*n))
y =z*exp(2)*(z+exp(2))/(z-exp(2))^3
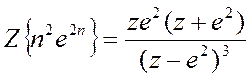
в) Z-преобразование
последовательности ![]() :
:
symsn
y= ztrans(cos(n).^2)
y=(z^2+z-3*z*cos(1)^2+cos(1)^2)*z/(z^3+z^2-4*z^2*cos(1)^2-z+4*z*cos(1)^2-1)
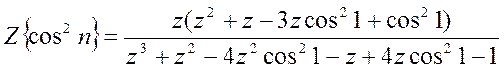
4. Определение сигнала во временной области (оригинал) по его Z – преобразованию, используя функцию iztrans() Matlab:
а)
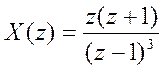 ,
,
б)
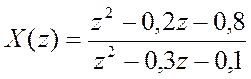 .
.
а) Сигнал, имеющий Z-преобразование
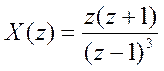 :
:
symsz
y= iztrans(z*(z+1)/(z-1).^3)
y =n^2
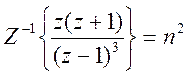
б) Сигнал, имеющий Z-преобразование
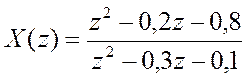 :
:
syms z
y= iztrans((z.^2-0.2*z-0.8)/(z.^2-0.3*z-0.1))
ans =8*charfcn[0](n)-36/7*(-1/5)^n-13/7*(1/2)^n
charfcn[0] – единичный импульс, где ненулевое значение только в точке равной нулю.
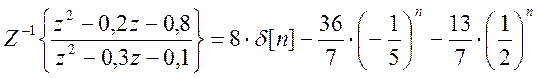
5. Разложение функции рационального Z – преобразования на простые дроби (индивидуальное задание, Приложение 1) с помощью функции residuez(). Нахождение аналитически обратного Z – преобразования, используя это разложение. Проверка результата с помощью iztrans().
Задание:
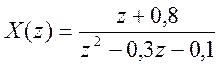
Функция ![]() выполняет разложение на простые
дроби рациональной Z-функции с вектором коэффициентов
полинома числителя num и вектора коэффициентов полинома
знаменателя den. Результат функции: r
– вектор вычетов, p – вектор полюсов, k
– вектор коэффициентов целой части разложения.
выполняет разложение на простые
дроби рациональной Z-функции с вектором коэффициентов
полинома числителя num и вектора коэффициентов полинома
знаменателя den. Результат функции: r
– вектор вычетов, p – вектор полюсов, k
– вектор коэффициентов целой части разложения.
Разложение на простые дроби:
num = [0,1,0.8];
den = [1,-0.3,-0.1];
[r,p,k] = residuez(num,den)
r = 3.7143 p = 0.5000 k = -8
4.2857 -0.2000
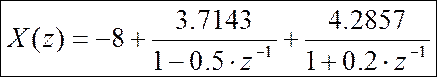
Обратное Z-преобразование:
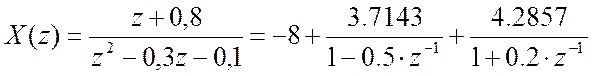
Поскольку 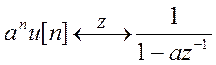 , то
, то 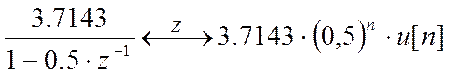 и
и
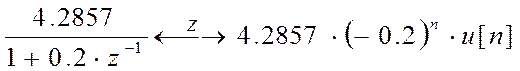 , а т.к.
, а т.к. ![]() ,
то
,
то ![]() .
.
![]() .
.
Проверка:
syms z
y= iztrans((z+0.8)/(z*z-0.3*z-0.1))
y =
-8*charfcn[0](n)+30/7*(-1/5)^n+26/7*(1/2)^n
что соответствует результату, полученному аналитически.
6. Решение с помощью Z– преобразования линейного разностного уравнения с постоянными коэффициентами (вариант – по индивидуальному заданию, Приложение 3):
8. ![]() .
.
Проверка правильности решения подстановкой в исходное уравнение.
Свойство временного сдвига:
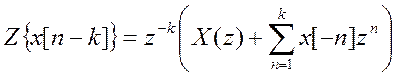
Z-преобразование от уравнения, с учётом свойства временного сдвига:
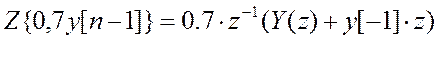
Z-преобразование входного
сигнала: ![]()
Решение
в Z-области с учётом начальных условий ![]() :
:
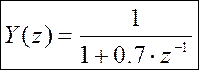
Обратное Z-преобразование:
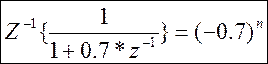
Проверка:
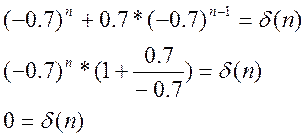
7.
Выражения прямого и обратного дискретно-временного преобразования Фурье (ДВПФ).
Связь ДВПФ и Z – преобразования.
Вычисление аналитически Z – преобразования
и ДВПФ сигнала:
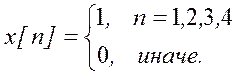
Прямое ДВПФ сигнала (для дискретных систем):
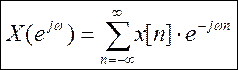
Обратное ДВПФ сигнала:
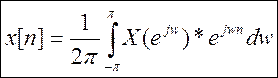
Дискретно – временное преобразование Фурье представляет собой Z - преобразование на единичной окружности z– плоскости.
ДВПФ сигнала:
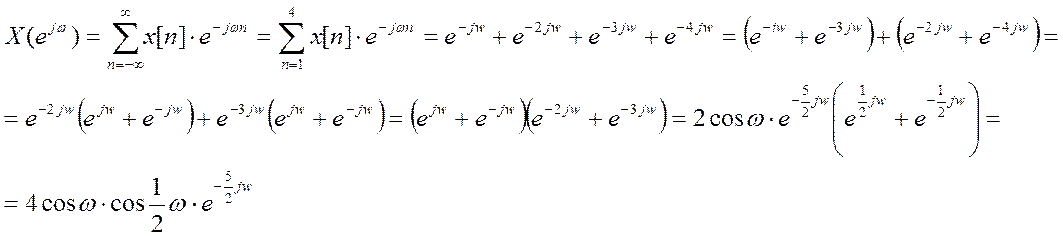
Как видно
дискретному сигналу ![]() в соответствие ставится
непрерывная функция
в соответствие ставится
непрерывная функция ![]() . Сигнал представляется в
виде суммы комплексных гармоник с амплитудами равными значениям дискретного
сигнала. Т.о. можно сделать вывод, что ДВПФ - это ряд Фурье по переменной
. Сигнал представляется в
виде суммы комплексных гармоник с амплитудами равными значениям дискретного
сигнала. Т.о. можно сделать вывод, что ДВПФ - это ряд Фурье по переменной ![]() , а коэффициентами этого ряда
являются значения дискретного сигнала.
, а коэффициентами этого ряда
являются значения дискретного сигнала.
Z – преобразование:
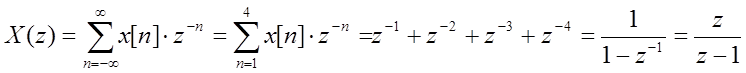
ОС: ![]()
8. Нахождение с помощью программы из Приложения 5 ДВПФ сигналов:
а) x[n] = e -0,5n,
б) 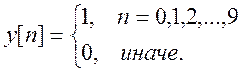
в)
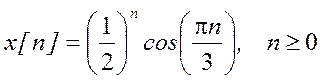
для
значения M = 64.
Построение графиков сигналов и амплитудного и фазового спектров этих сигналов.
а)
ДВПФ сигнала ![]() :
:
n=0:20;
x=exp(-0.5*n);
[X,w]=DTFT(x,64);
subplot(211)
plot(w,abs(X)),
title('Amplitude spectrum {exp}^{-0.5*{\itn}} '),grid ,
subplot(212)
plot(w,angle(X)),
title('Phase spectrum {\itx} = {exp}^{-0.5*{\itn}} '), grid ,
xlabel('w, rad/sec')
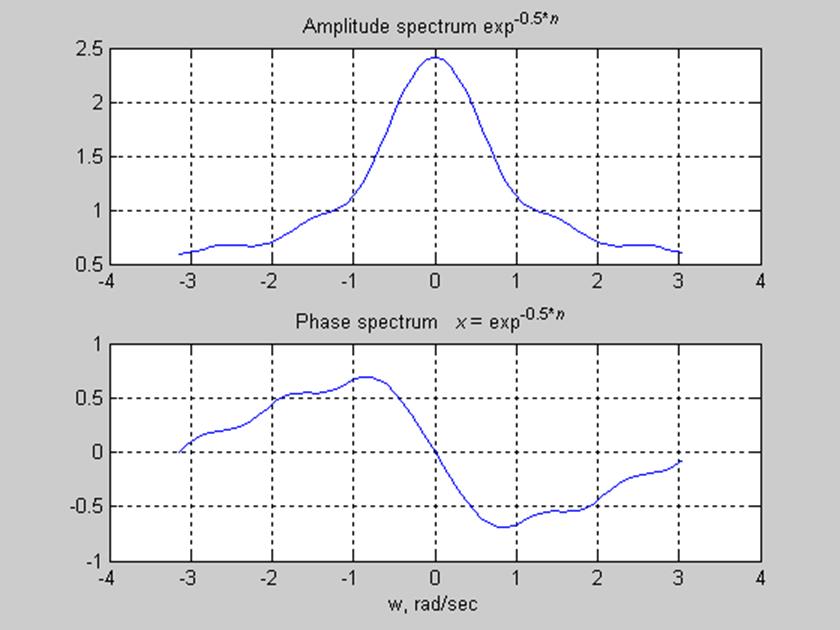
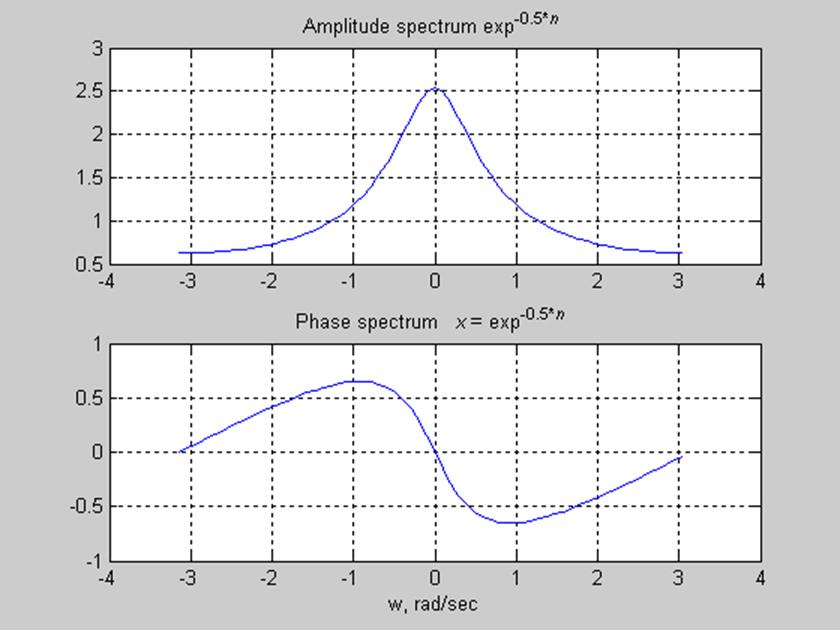
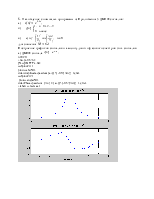
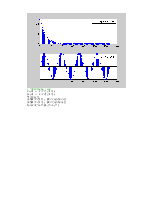
Рис.1. Амплитудный и фазовый
спектры сигнала ![]() ,
при n=5 и 20
,
при n=5 и 20
ДВПФ является периодической
функцией с периодом ![]() ,
поэтому достаточным было отобразить фазовый и амплитудный спектры в интервале
,
поэтому достаточным было отобразить фазовый и амплитудный спектры в интервале ![]() . Как видно из графиков,
амплитудный спектр ДВПФ – чётная функция, а фазовый спектр – нечётная функция.
. Как видно из графиков,
амплитудный спектр ДВПФ – чётная функция, а фазовый спектр – нечётная функция.
![]() - дискретная функция,
- дискретная функция, ![]() - непрерывная функция.
- непрерывная функция.
б)
ДВПФ сигнала 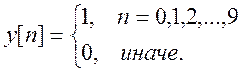 :
:
n=1:9;
x(n)=1;
[X,w]=DTFT(x,64);
subplot(211)
plot(w,abs(X)),
title('Amplitude spectrum x(n)=1 '),grid ,
subplot(212)
plot(w,angle(X)),
title('Phase spectrum x(n)=1 '), grid ,
xlabel('w, rad/sec'),
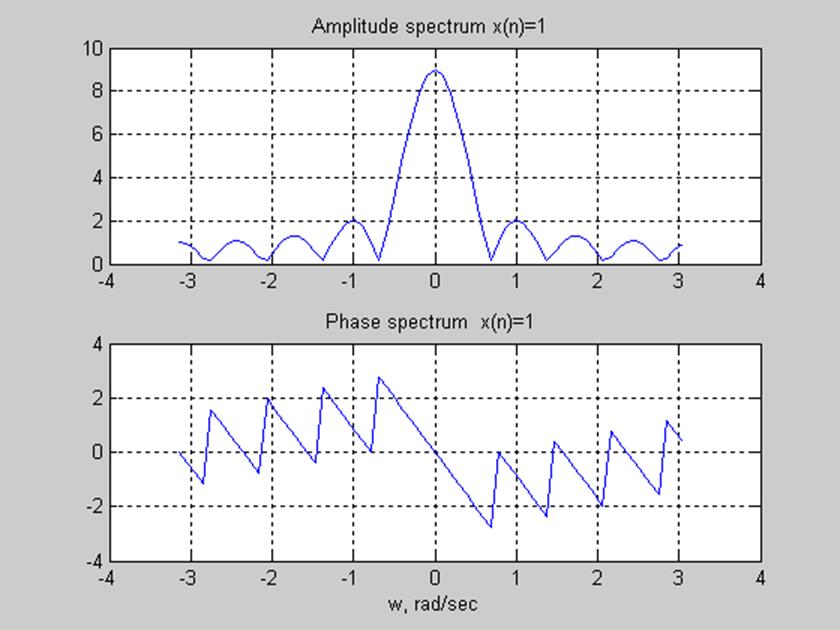
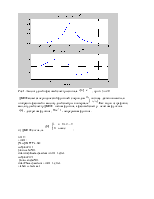
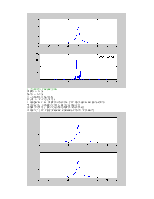
Рис.2. Амплитудный и фазовый
спектры сигнала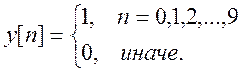
Для непрерывного прямоугольного импульса преобразование Фурье имеет аналогичный вид с единственным отличием: график спектральной плотности – функция непериодическая.
ДВПФ
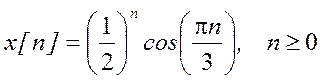 :
:
n=1:20;
x(n)=(power(0.5,n)).*cos(pi*n/3);
[X,w]=DTFT(x,64);
subplot(211)
plot(w,abs(X)),
title('Amplitude spectrum '),grid ,
subplot(212)
plot(w,angle(X)),
title('Phase spectrum '), grid ,
xlabel('w, rad/sec'),
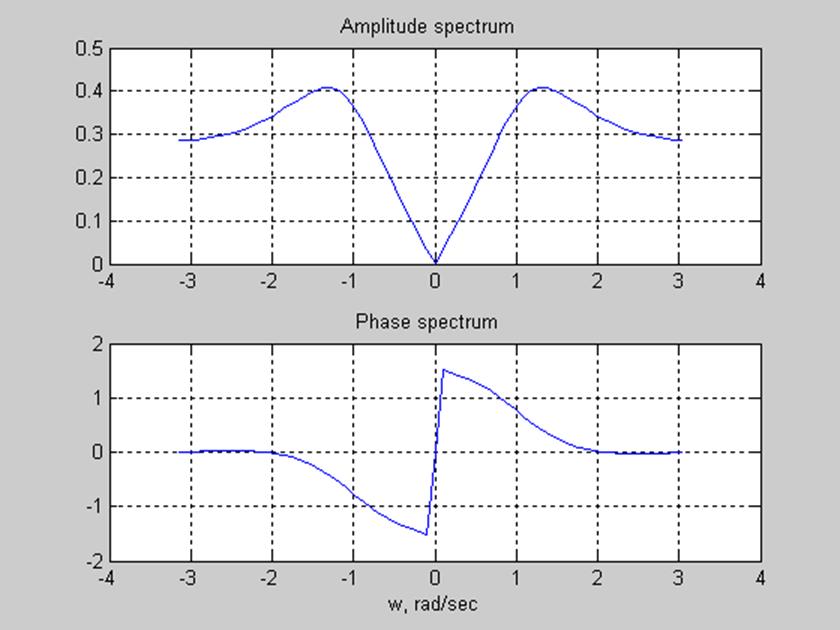
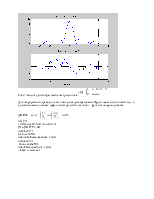
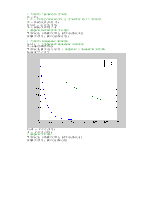
Рис.3. Амплитудный и фазовый
спектры сигнала 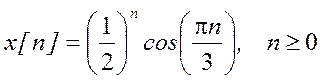
9. Программа из Приложения 6, иллюстрирующая некоторые из свойств ДВПФ.
Приложение 6. Процедура иллюстрации
свойств ДВПФ
N = 128; % Длина сигналов
k = 0:N-1;
gamma = -0.1;
g = exp(gamma*k);
% g - экспоненциальная функция
h = sin(2*pi*k/(N/4));
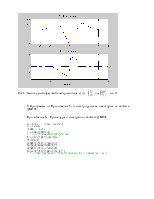
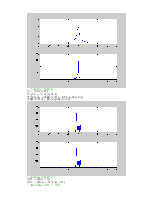
figure(1)
subplot(211),stem(k,g)
legend('exp(gamma*k)')
subplot(212),stem(k,h)
legend('sin(2*pi*k/(N/4))')
% h - синусоидальная последовательность с периодом = N/4
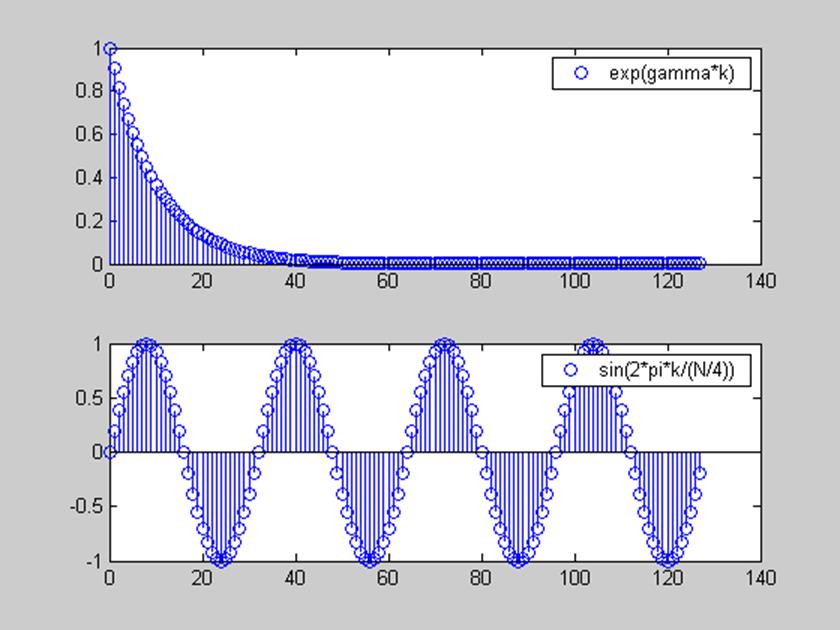
% вычисление ДВПФ
[G,w] = DTFT(g,512);
[H,w] = DTFT(h,512);
figure(2)
subplot(211), plot(w,abs(G))
subplot(212), plot(w,abs(H))
legend('w=2*pi/32=0,2')
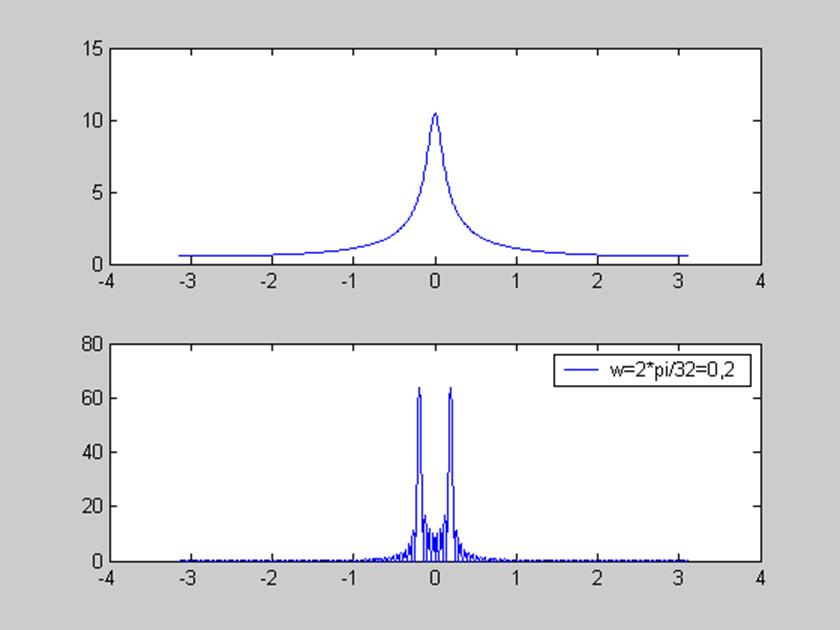
% Свойство линейности
alpha = 0.5;
beta = 0.25;
y = alpha*g+beta*h;
[Y,w] = DTFT(y,512);
% Графики Y и alpha*G+beta*H для проверки их равенства
figure(3), subplot(211),plot(w,abs(Y))
subplot(212), plot(w,abs(alpha*G+beta*H))
%input(' Для продолжения нажмите любую клавишу')
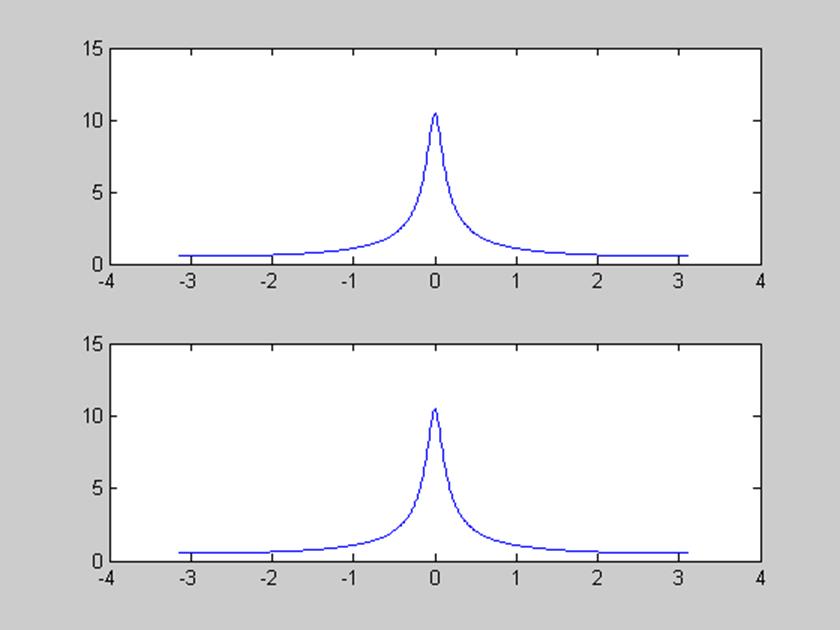
% Свойство временного сдвига
n0 = 12;
% y2 - последовательность y, сдвинутая на 12 отсчетов
y2 = [zeros([1,n0]) g];
[Y2,w] = DTFT(y2,512);
G0 = exp(-j*w*n0).*G;
% Графики амплитудных спектров
figure(3), subplot(211), plot(w,abs(G0))
subplot(212), plot(w,abs(Y2));
% Свойство изменения масштаба
a=0.1; % Коэффициент изменения масштаба
g1= exp(gamma*k*a);
figure(4),plot(k,g,k,g1) % Графики во временной области
legend('g','g1')
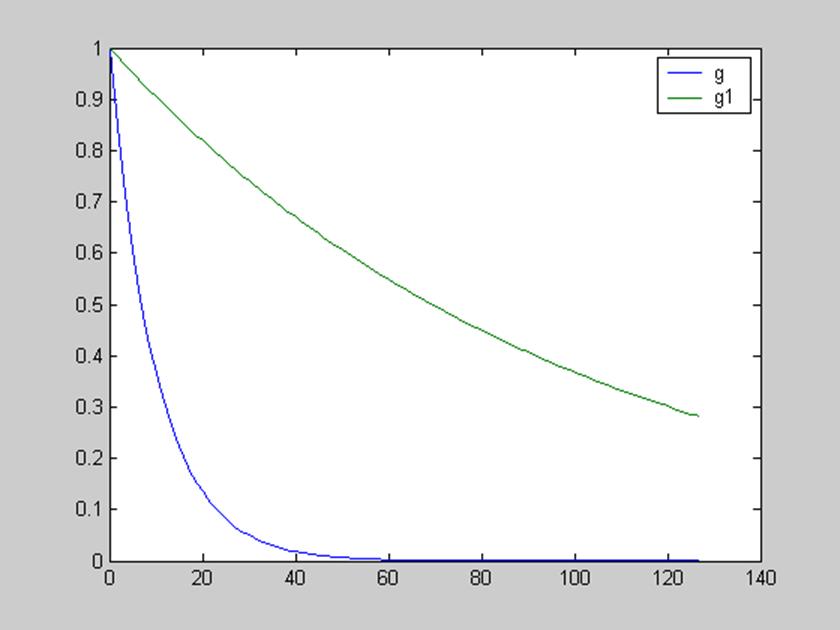
[G,w] = DTFT(g,512);
G1 = DTFT(g1,512);
% Графики спектров
figure(5), subplot(211), plot(w,abs(G))
subplot(212), plot(w,abs(G1))
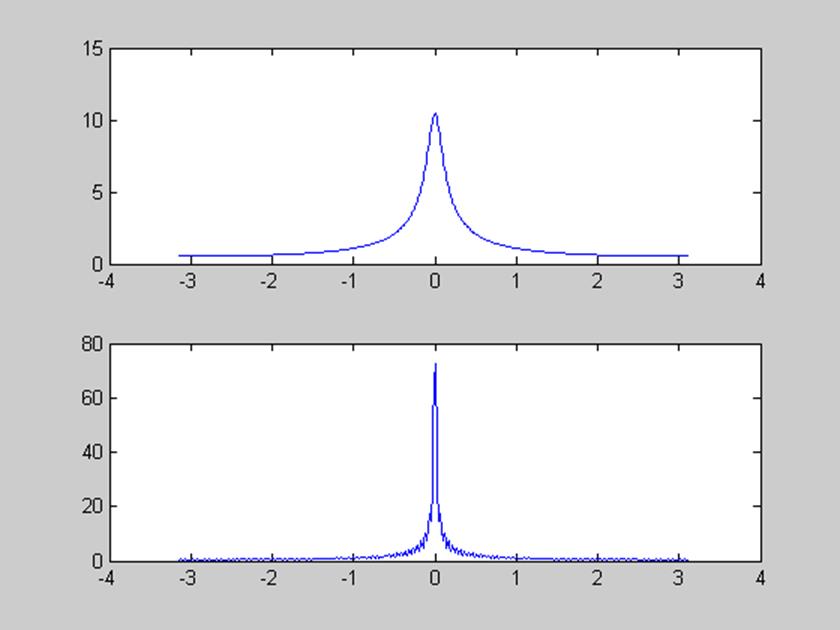
% Свойство свертки
y5 = conv(g,h);
[Y5,w] = DTFT(y5,512);
figure(6), subplot(211), plot(w,abs(Y5))
subplot(212), plot(w,abs(G.*H))
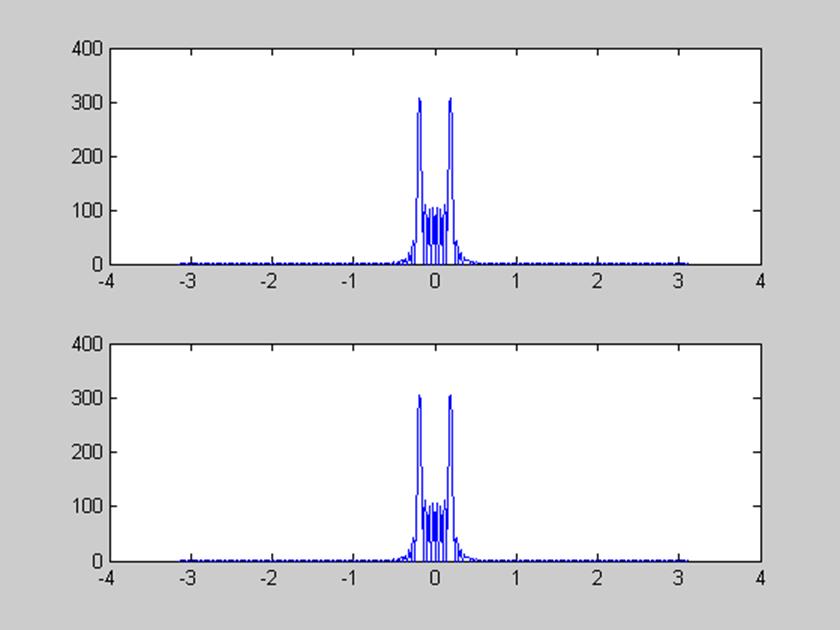
% Теорема Парсеваля
val1 = sum(g.*g);
val2 = sum(G.*conj(G))/512;
% Сравнение val1 с val2
disp('Разность val1-val2 = ')
disp(val1-val2)
Разность val1-val2 =
-8.8818e-016
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.