

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов»
ЛАБОРАТОРНАЯ РАБОТА № 7
ЛИНЕЙНЫЕ НЕПРЕРЫВНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
Группа: АТ-23 Преподаватель:
Студенты: Рыбкина А. Щетинин Ю.И.
Кудрина Е.
Новосибирск, 2004
ЛИНЕЙНЫЕ НЕПРЕРЫВНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
Цель работы:знакомство с динамическими характеристиками линейных непрерывных стационарных (инвариантных во времени) систем и их использованием для анализа систем в среде MATLAB.
1.
Определим передаточную функцию активного фильтра. При этом операционный усилитель предполагается идеальным с бесконечно большим коэффициентом усиления и бесконечным входным сопротивлением.
Схема фильтра:
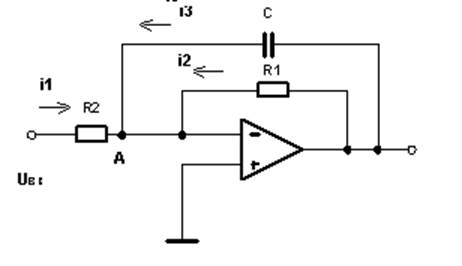
R1=10 кОм, R2=500 Ом,
C=0,1 мкФ
Первый закон Кирхгофа для узла А:
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
Отношение выходного напряжения к входному:
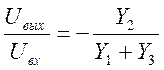
Для рассматриваемого фильтра:
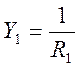
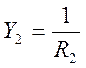
![]()
Передаточная функция данного фильтра, как отношение преобразований Лапласа выходного и входного сигнала, имеет вид:
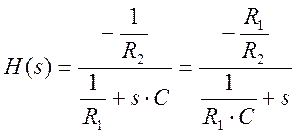
Если подставить значения параметров, то получим:
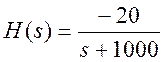 .
.
2.
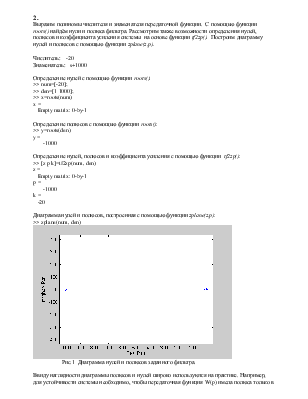
Выразим полиномы числителя и знаменателя передаточной функции. С помощью функции roots() найдём нули и полюса фильтра. Рассмотрим также возможности определения нулей, полюсов и коэффициента усиления системы на основе функции tf2zp(). Построим диаграмму нулей и полюсов с помощью функции zplane(z,p).
Числитель: -20
Знаменатель: s+1000
Определение нулей с помощью функции roots():
>> num=[-20];
>> den=[1 1000];
>> x=roots(num)
x =
Empty matrix: 0-by-1
Определение полюсов с помощью функции roots():
>> y=roots(den)
y =
-1000
Определение нулей, полюсов и коэффициента усиления с помощью функции tf2zp():
>> [z p k]=tf2zp(num, den)
z =
Empty matrix: 0-by-1
p =
-1000
k =
-20
Диаграмма нулей и полюсов, построенная с помощью функции zplane(z,p):
>> zplane(num, den)
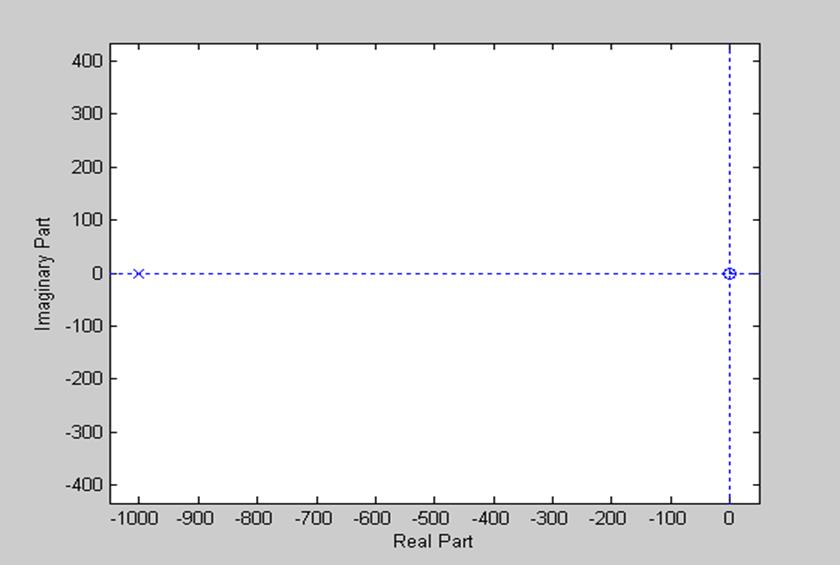
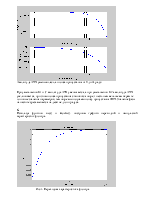
Рис.1 Диаграмма нулей и полюсов заданного фильтра.
Ввиду наглядности диаграммы полюсов и нулей широко используются на практике. Например, для устойчивости системы необходимо, чтобы передаточная функция W(p) имела полюса только в левой полуплоскости переменной p. Таким образом, по расположению полюсов передаточной функции можно судить об устойчивости системы.
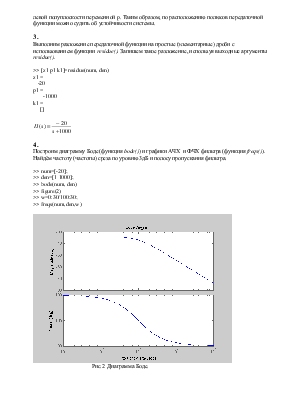
3.
Выполним разложение передаточной функции на простые (элементарные) дроби с использованием функции residue(). Запишем такое разложение, используя выходные аргументы residue().
>> [z1 p1 k1]=residue(num, den)
z1 =
-20
p1 =
-1000
k1 =
[]
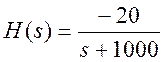
4.
Построим диаграмму Боде (функция bode()) и графики АЧХ и ФЧХ фильтра (функция freqs()). Найдём частоту (частоты) среза по уровню 3дБ и полосу пропускания фильтра.
>> num=[-20];
>> den=[1 1000];
>> bode(num, den)
>> figure(2)
>> w=0:30/100:30;
>> freqs(num,den,w)
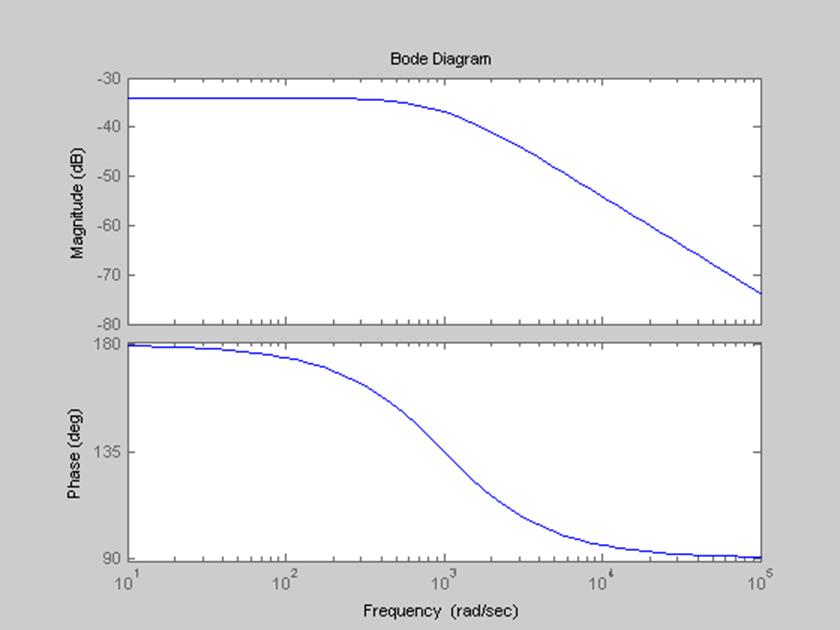
Рис.2 Диаграмма Боде.
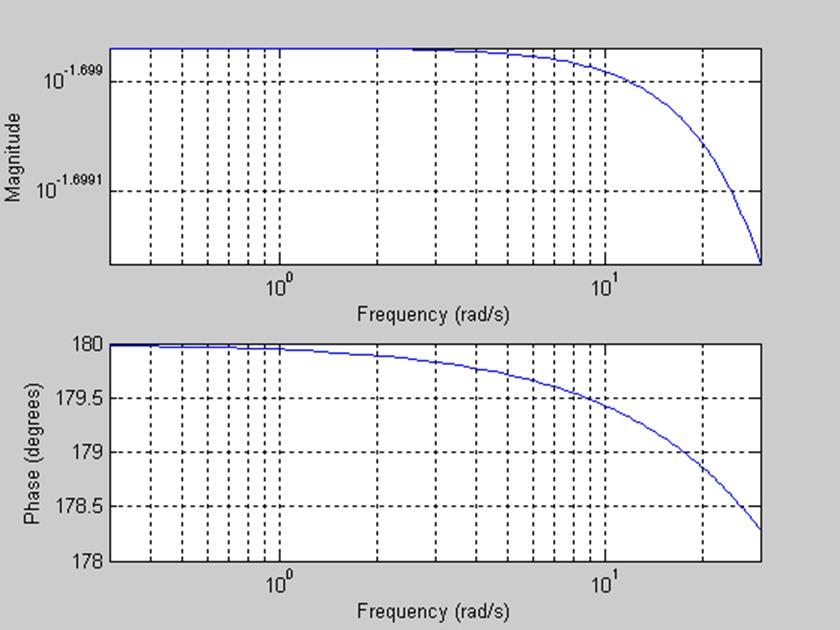
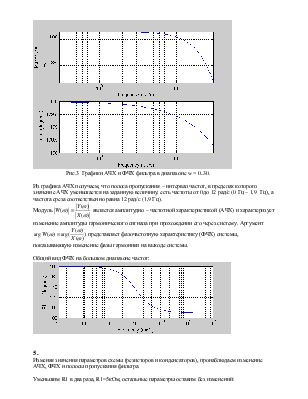
Рис.3 Графики АЧХ и ФЧХ фильтра в диапазоне w = 0..30.
Из графика АЧХ получаем, что полоса пропускания – интервал частот, в пределах которого значение АЧХ уменьшается на заданную величину, есть частоты от 0 до 12 рад/с (0 Гц – 1,9 Гц), а частота среза соответственно равна 12 рад/с (1,9 Гц).
Модуль 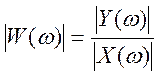 является
амплитудно – частотной характеристикой (АЧХ) и характеризует изменение
амплитуды гармонического сигнала при прохождении его через систему. Аргумент
является
амплитудно – частотной характеристикой (АЧХ) и характеризует изменение
амплитуды гармонического сигнала при прохождении его через систему. Аргумент 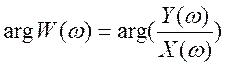 представляет
фазочастотную характеристику (ФЧХ) системы, показывающую изменение фазы
гармоники на выходе системы.
представляет
фазочастотную характеристику (ФЧХ) системы, показывающую изменение фазы
гармоники на выходе системы.
Общий вид ФЧХ на большом диапазоне частот:
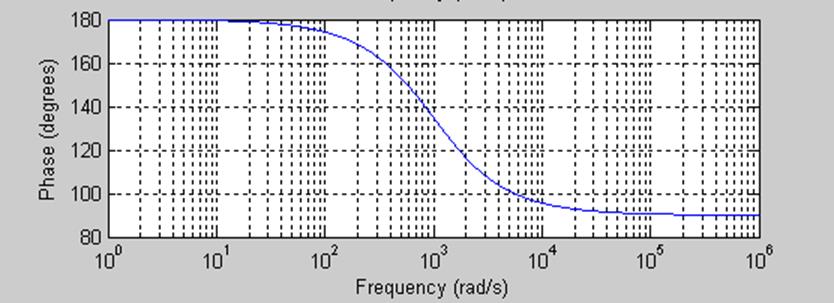
5.
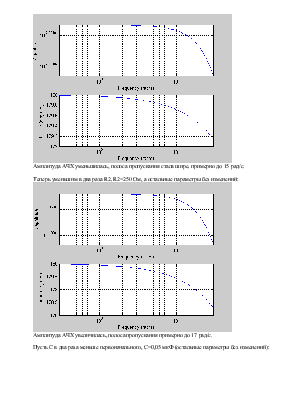
Изменяя значения параметров схемы (резисторов и конденсаторов), пронаблюдаем изменение АЧХ, ФЧХ и полосы пропускания фильтра.
Уменьшим R1 в два раза, R1=5кОм, остальные параметры оставим без изменений:
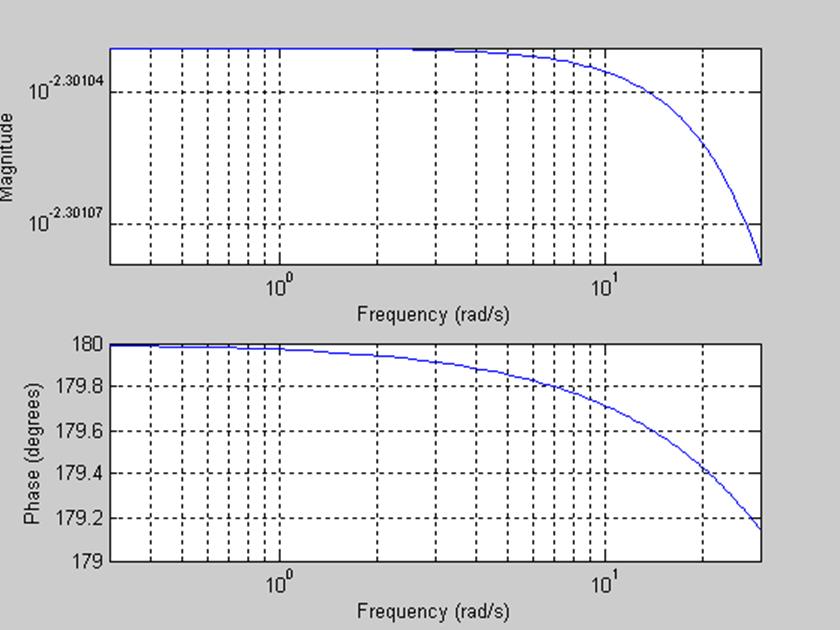
Амплитуда АЧХ уменьшилась, полоса пропускания стала шире, примерно до 15 рад/с.
Теперь уменьшим в два раза R2, R2=250 Ом, а остальные параметры без изменений:
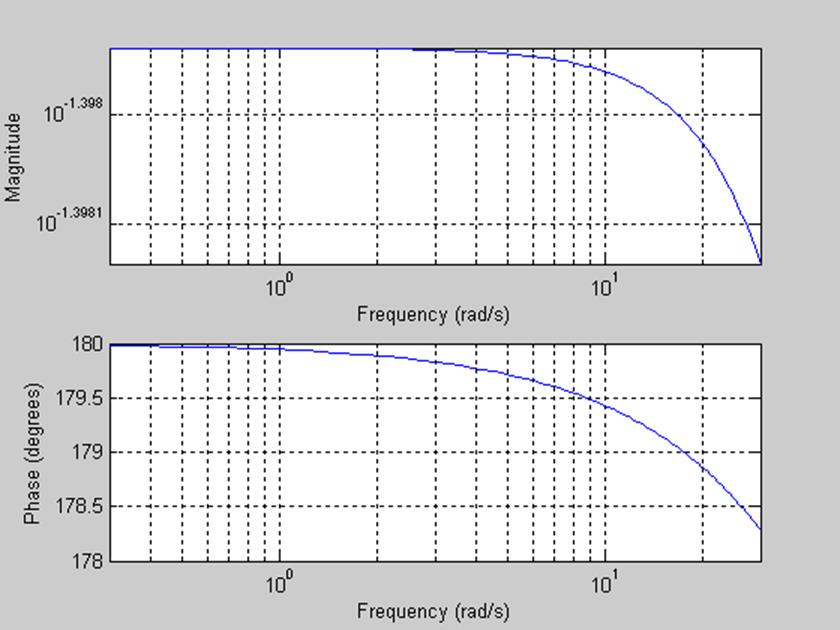
Амплитуда АЧХ увеличилась, полоса пропускания примерно до 17 рад/с.
Пусть C в два раза меньше первоначального, С=0,05 мкФ (остальные параметры без изменений):
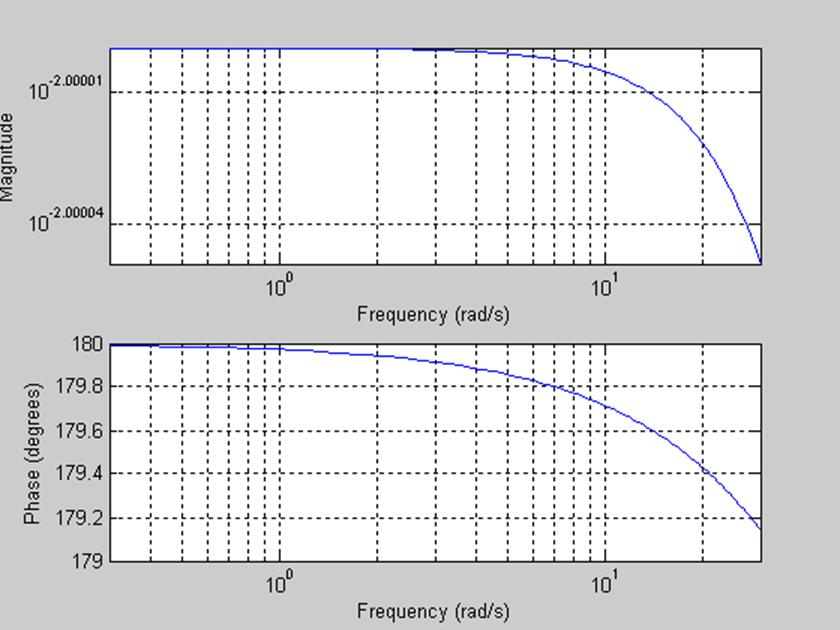
Амплитуда АЧХ уменьшилась, а полоса пропускания от 0 до 14 рад/с.
При уменьшении R1 и С амплитуда АЧХ уменьшается, а при уменьшении R2 амплитуда АЧХ увеличивается, при этом полоса пропускания становится шире, то есть чем меньше мы берём те или иные значения параметров, тем шире мы получаем полосу пропускания ФНЧ. Значение фазы на частоте среза меняется на десятые доли градуса.
6.
Используя функции step() и impulse(), построим графики переходной и импульсной характеристик фильтра.
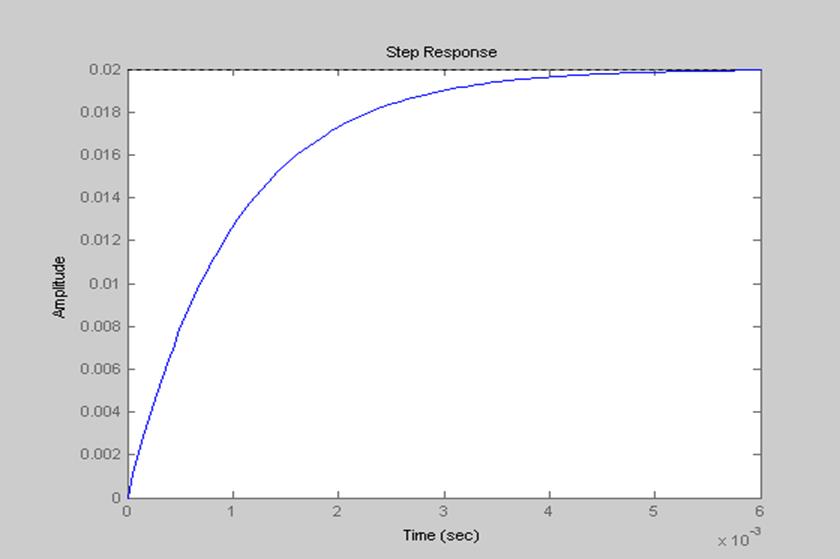
Рис. 4 Переходная характеристика фильтра
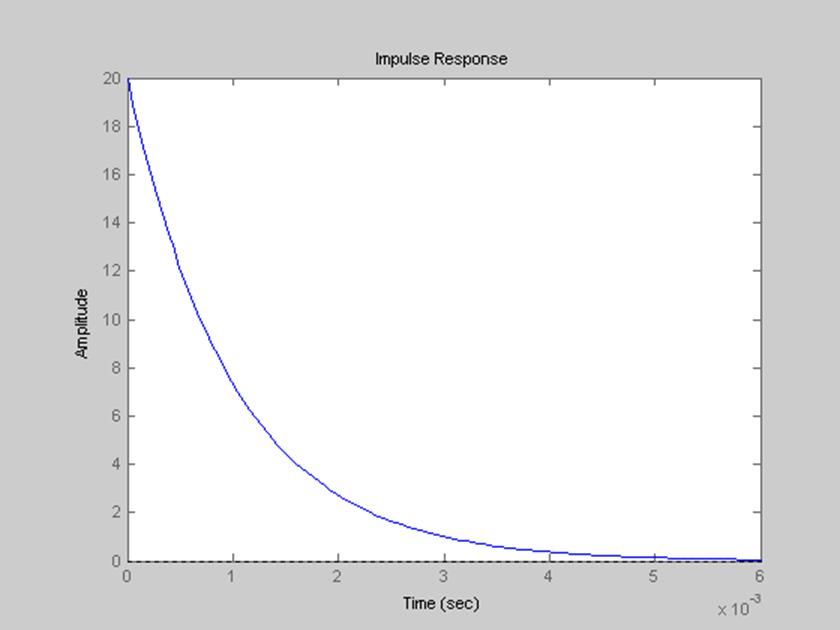
Рис. 5 Импульсная характеристика фильтра.
Импульсная
характеристика – реакция на входной сигнал в виде δ-функции при нулевых
начальных условиях. Переходная характеристика – реакция системы на входное
воздействие в виде единичной ступенчатой функции при нулевых начальных
условиях. Так как дельта-функция может рассматриваться как производная от
единичной, то переходная и весовая функция связаны соотношением 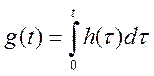 . Из
этого выражения следует, что время нарастания переходной характеристики
определяется длительностью весовой функции системы. Переходная функция чаще
используется в экспериментальной практике, так как практически дельта-функцию
можно сформировать только приближённо, а ступенчатую функцию – достаточно
точно.
. Из
этого выражения следует, что время нарастания переходной характеристики
определяется длительностью весовой функции системы. Переходная функция чаще
используется в экспериментальной практике, так как практически дельта-функцию
можно сформировать только приближённо, а ступенчатую функцию – достаточно
точно.
7.
Определим входной гармонический сигнал с частотой, входящей в полосу пропускания фильтра. Используя функцию lsim(), найдём отклик (выходной сигнал) системы на данный входной сигнал. Построим графики входного и выходного сигналов. Сделаем аналитическую оценку выходного сигнала, базируясь на частотных характеристиках системы.
В полосу пропускания входит частота 1 Гц, поэтому зададим входной гармонический сигнал как cos(2*pi*t), тогда будет получен следующий результат:
>> num=20;
>> den=[1 1000];
>> t=linspace(0,5,301);
>> u=cos(2*pi*t);
>> lsim(num,den,u,t)
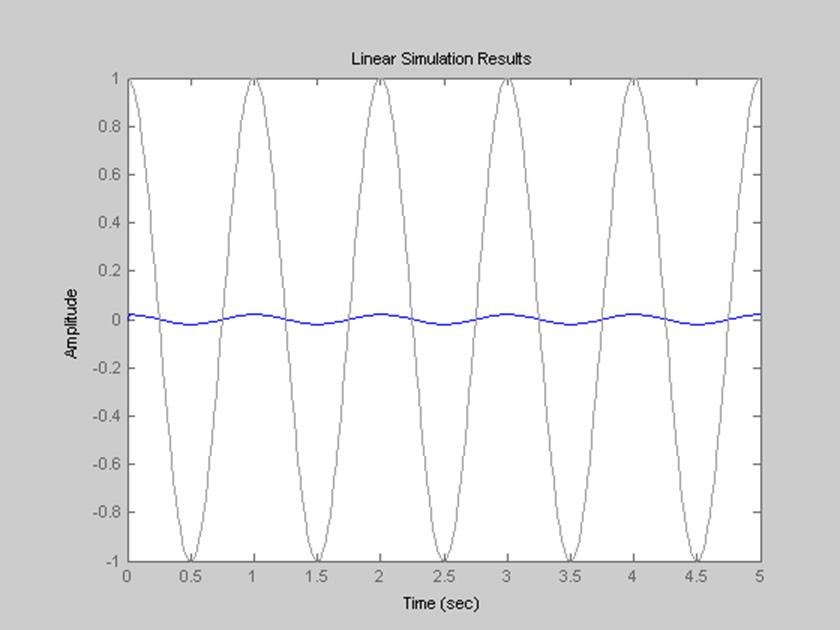
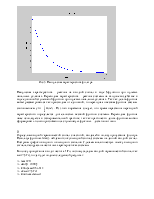
Рис. 6 Входной гармонический сигнал и отклик на него.
Аналитически оценим выходной сигнал:
![]()
Из графика АЧХ определяем, что амплитуда порядка 0,02, а из ФЧХ видно, что фаза 180º. Получаем, что y(t)=0,02cos(2πt+π)=0,02cos(2πt). Мы видим, что этот результат полностью соответствует виду сигнала, полученного на графике, то есть сигнал на выходе имеет такую же форму, как и входной сигнал, но его амплитуда составляет 0,02 (в 50 раз меньше, чем у входного сигнала).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.