Министерство Образования и Науки Российской Федерации
Новосибирский Государственный Технический Университет
Факультет Автоматики и Вычислительной Техники
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория информационных процессов и систем»
Лабораторная работа № 3
Вычисление определенных интегралов в среде MatLAB
Студент: Преподаватель:
Осадчая Д.А. проф. Рабинович Е.В.
Группа: АТ-63
Новосибирск, 2009
Ознакомиться с некоторыми средствами математического анализа в среде MatLAB. Изучить предоставляемые пакетом возможности по вычислению определенных интегралов, дифференцированию и аналитическим вычислениям.
1) Вычисление значения производной в заданной точке.
Листинг m-файла для вычисления значения производной в заданной точке:
function[] = z1(f,x0)
syms x y y_dif
switch(f)
case ('exp')
y=exp(x);
case ('log')
y=log(x);
case ('stepen')
a=input('Введите основание: ')
y=a^x;
otherwise
disp('Неизвестный вид функции!')
break
end
y_dif=diff(y)
C=inline(y_dif);
res=C(x0)% значение производной
Результат выполнения функции:
Экспоненциальная функция:
z1('log',4)
y_dif =1/x
res =0.2500
Логарифмическая функция:
z1('exp',2)
y_dif =exp(x)
res = 7.3891
Степенная функция:
z1('stepen',2)
Введите основание: 2
a =2
y_dif =2^x*log(2)
res =2.7726
2) Вычисление площади фигуры, ограниченной полиномом второй степени.
Листинг m-файла для вычисления площади фигуры:
function[square]=z2(a,b,c,left,right)
x = left:0.01:right;
y = a*(x.*x)+b*x+c;
S = trapz(x, abs(y));
hold on;
x1 = left-1:0.01:right+1;
y1 = a*(x1.*x1)+b*x1+c;
plot (x1,y1, 'r');
stem (x,y);
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),
title('Фигура, ограниченная полиномом второго порядка')
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),
legend('Функция y(x)','Фигура площадью S',2);
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),
xlabel('X');
ylabel('Y');
grid;
square = S
Результат выполнения функции:
s1=z2(1,1,5,-1,0.5)
s1 = 7.5000
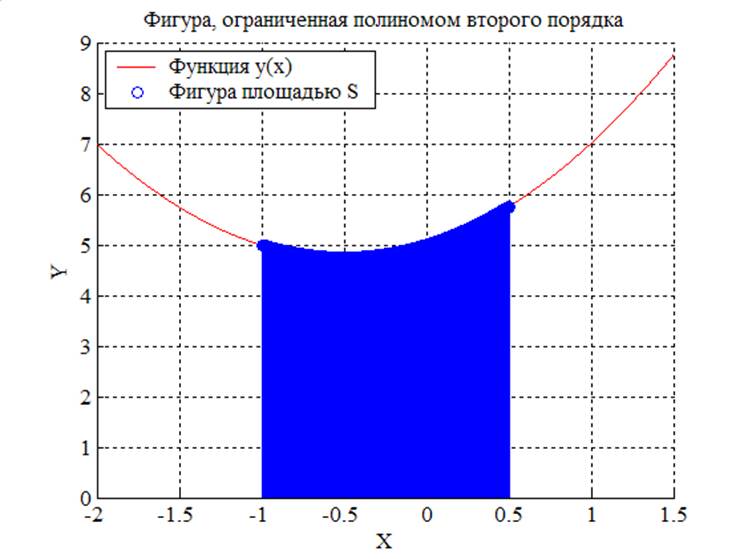
Рис. 1. Фигура, ограниченная графиком функции y= x2+x+5 и прямыми x=-1, x=0.5
3) Вычисление производной полинома второй степени.
Листинг m-файла для вычисления производной полинома 2-ой степени и построения графиков полинома и его производной:
function z3(a,b,c)
x = -5:1:5;
y = a*(x.*x)+b*x+c;
plot(x,y)
hold on
p=[a b c];
q=polyder(p);
y1=q(1).*x+q(2);
plot(x,y1,'r')
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),
legend('Полином второго порядка','Его производная',2)
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),
title('Нахождение производной полинома второго порядка')
grid
syms x y y_d
y = a*x.^2+b*x+c;
y_dif= diff(y)
Результат выполнения функции:
z3(1,2,4)
y_dif =2*x+2
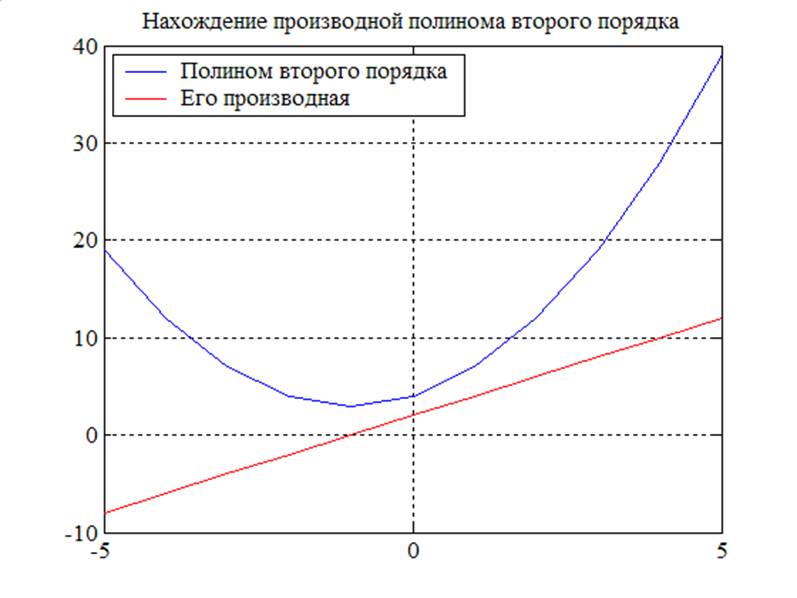
Рис. 2. График функции y= x2+2x+4 и ее производной y=2x+2
4) Нахождение экстремумов полиномов 3-го порядка
Листинг m-файла для нахождения экстремума полинома 3-го порядка:
function z4(a,b,c,d)
x=-20:0.1:20;
y=a*x.^3+b*x.^2+c*x+d;
plot(x,y)
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),
title('Нахождение экстремумов полинома');
xlabel('Ось Х')
ylabel('Ось Y')
grid
hold on
p=[a b c d];
q=polyder(p);
x0=roots(q)
y0=a*x0.^3+b*x0.^2+c*x0+d
plot(x0,y0,'rx')
x1=[-20 20];
y1=a*x1.^3+b*x1.^2+c*x1+d;
plot(x1,y1,'rx')
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),
legend('Полином третьей степени', 'Экстремумы полинома', 2)
Результат выполнения функции:
z4(1,2,4,10)
x0 =-0.6667 + 0.9428i -0.6667 - 0.9428i
y0 =7.9259 + 1.6761i 7.9259 - 1.6761i
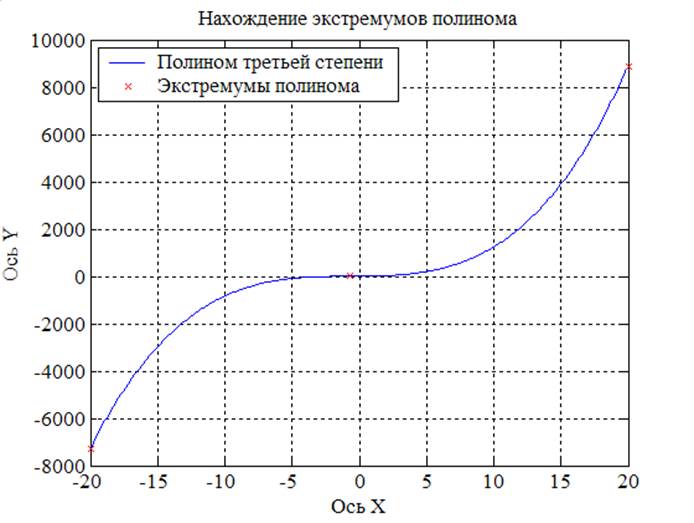
Рис. 3. График функции y=x3+2x2+4x+10 и ее экстремумы.
5) Вычисление интеграла заданных функций.
Листинг m-файла для вычисления интеграла:
function z5(f,left,right)
x=left:0.01:right;
switch(f)
case ('exp')
y=exp(x);
case ('log')
y=log(x);
case ('stepen')
a=input('Введите основание: ');
y=a.^x;
otherwise
disp('Неизвестная функция!')
break
end
S = trapz(x, abs(y))
Результат выполнения функции:
Логарифмическая функция:
z5('log',1,2)
S=0.3863
Экспоненциальная функция:
z5('exp',1,2)
S=4.6708
Степенная функция:
z5('stepen',-1,2)
Введите основание:4
S=11.3614
6) Вычисление скорости и ускорения физического тела, которое движется по кривой описываемой полиномом третьей степени, в заданной точке.
Листинг m-файла для вычисления скорости и ускорения физического тела:
function z6(a,b,c,d,x0)
y0=a*x0.^3+b*x0.^2+c*x0+d;
p=[a b c d];
v=polyder(p); % уравнение скорости
v0=v(1)*x0.^2+v(2)*x0+v(3)
asc=polyder(v); % уравнение ускорения
a0=asc(1)*x0+asc(2)
x=-10:0.1:10;
y=a*x.^3+b*x.^2+c*x+d;
v=v(1)*x.^2+v(2)*x+v(3);
asc=asc(1)*x+asc(2);
subplot(211)
plot(x,y)
hold on
plot(x0,y0,'rx')
title('График траектории')
xlabel('X'), ylabel('S'), grid
legend('Траектория','Заданная точка',1)
subplot(223)
plot(x,v)
hold on
plot(x0,v0,'rx')
title('График скорости')
xlabel('X'), ylabel('v'), grid
legend('Скорость','Заданная точка',2)
subplot(224)
plot(x,asc)
hold on
plot(x0,a0,'rx')
title('График ускорения')
xlabel('X'), ylabel('a'), grid
legend('Ускорение','Заданная точка',2)
Результат выполнения функции:
z6(1,2,4,10,3)
v0 =43
a0 =22
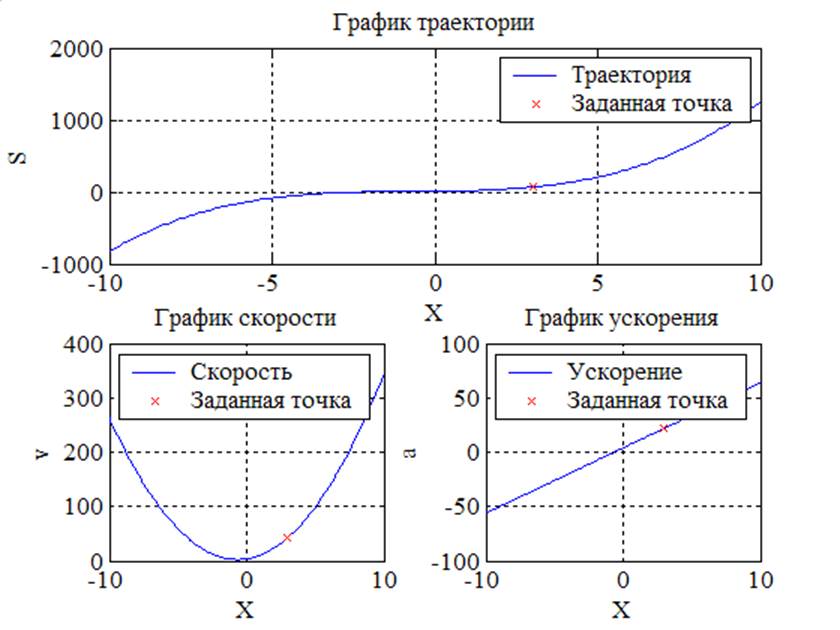
Рис. 4. Графики траектории, скорости и ускорения физического тела, которое движется по кривой y=x3+2x2+4x+10 в точке x=3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.