






Неустановившимся (нестационарным)
называется такое движение жидкости, при котором в каждой фиксированной точке
потока скорость и давление являются функциями не только координат, но и
времени, т.е. ![]() ,
, ![]() ,
где
,
где ![]() и
и![]() - скорость и давление в
точке потока. При напорном неустановившемся движении расход в данный момент
времени во всех сечениях потока одинаков.
- скорость и давление в
точке потока. При напорном неустановившемся движении расход в данный момент
времени во всех сечениях потока одинаков.
Энергетическое уравнение (уравнение Бернулли) для напорного неустановившегося движения записывается в следующем виде:
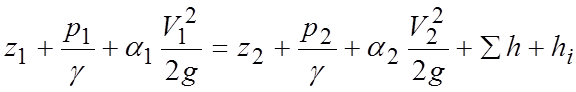 ,
(7.1)
,
(7.1)
где
![]() - инерционный напор, который для потока
в цилиндрической трубе равен
- инерционный напор, который для потока
в цилиндрической трубе равен
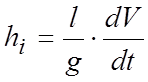 .
.
Остальные члены уравнения (7.1) имеют те же значения, что и в (4.3), но применительно к данному моменту времени.
Потери напора ![]() подсчитываются
приближенно по формулам (4.4) и (4.6) для установившегося равномерного
движения. Инерционный напор является положительным в том случае, когда
подсчитываются
приближенно по формулам (4.4) и (4.6) для установившегося равномерного
движения. Инерционный напор является положительным в том случае, когда ![]() , и отрицательным – при
, и отрицательным – при ![]() .
.
В данном сечении неустановившегося потока закон изменения средней скорости во времени определяется уравнением
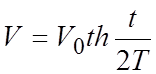 ,
,
где
![]() - скорость при установившемся
движении;
- скорость при установившемся
движении; ![]() - время;
- время; ![]() -
параметр, равный
-
параметр, равный
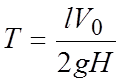 ,
,
где
![]() - напор, соответствующий скорости
- напор, соответствующий скорости ![]() .
.
При резком изменении во времени скорости движения жидкости, например, при быстром закрытии задвижки на трубопроводе, возникает комплекс явлений, называемый гидравлическим ударом, который характеризуется резким изменением давления и плотности жидкости и упругой деформацией стенки трубы (вплоть до ее разрушения). Различают два вида гидравлического удара:
1) прямой гидравлический удар, который имеет место при
![]() (
(![]() - время полного закрытия задвижки;
- время полного закрытия задвижки; ![]() - продолжительность фазы
гидравлического удара, т.е. время распространения ударной волны на участке
равном двойной длине трубы);
- продолжительность фазы
гидравлического удара, т.е. время распространения ударной волны на участке
равном двойной длине трубы);
2) непрямой гидравлический удар, который имеет место
при ![]() .
.
В случае прямого гидроудара давление жидкости
возрастает на величину ![]() , которая вычисляется по
формуле Жуковского:
, которая вычисляется по
формуле Жуковского:
![]() ,
(7.2)
,
(7.2)
где ![]() -
средняя скорость в трубе до удара; r
- плотность жидкости (до удара);
-
средняя скорость в трубе до удара; r
- плотность жидкости (до удара); ![]() - скорость
ударной волны.
- скорость
ударной волны.
В случае непрямого гидроудара (при линейном
изменении скорости ![]() ) приращение давления
) приращение давления ![]() приблизительно равно
приблизительно равно
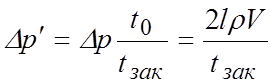 .
(7.3)
.
(7.3)
Скорость ![]() ударной волны
определяется по следующей формуле
ударной волны
определяется по следующей формуле
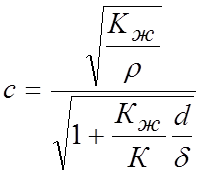 ,
(7.4)
,
(7.4)
где
![]() и
и ![]() -
модуль упругости жидкости и материала трубы;
-
модуль упругости жидкости и материала трубы; ![]() и
и
![]() - внутренний диаметр и толщина
стенки трубы.
- внутренний диаметр и толщина
стенки трубы.
При данной скорости ![]() продолжительность фазы гидроудара равна
продолжительность фазы гидроудара равна
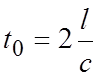 .
.
Значения модуля упругости некоторых жидкостей и материалов указаны в Приложении 7.
Пример 7.1. Определить
время закрытия задвижки, установленной на свободном конце стального водопровода
диаметром ![]() м, длиной
м, длиной ![]() м
с толщиной стенки
м
с толщиной стенки ![]() мм, при условии, чтобы
максимальное повышение давления в водопроводе было в три раза меньше, чем при
мгновенном закрытии задвижки. Через сколько времени после мгновенного закрытия
задвижки повышение давления распространится до сечения, находящегося на
расстоянии
мм, при условии, чтобы
максимальное повышение давления в водопроводе было в три раза меньше, чем при
мгновенном закрытии задвижки. Через сколько времени после мгновенного закрытия
задвижки повышение давления распространится до сечения, находящегося на
расстоянии ![]() от задвижки ?
от задвижки ?
Решение:
Время закрытия задвижки находим из уравнения (7.3).
Согласно условию задачи, максимальное повышение давления в водопроводе должно
быть в три раза меньше, чем при мгновенном закрытии задвижки, т.е. ![]() , где
, где ![]() -
приращение давления при прямом гидравлическом ударе. Величину
-
приращение давления при прямом гидравлическом ударе. Величину ![]() определяем по формуле Жуковского
(7.2).
определяем по формуле Жуковского
(7.2).
Таким образом, получим
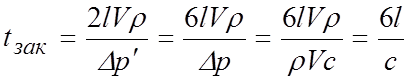 .
.
Скорость распространения ударной волны найдем из уравнения (7.4)
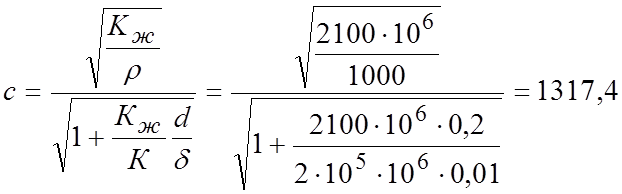 м/с.
м/с.
Следовательно, время закрытия задвижки
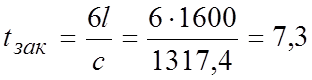 с.
с.
Найдем время, через которое повышение давления после
мгновенного закрытия задвижки распространится до сечения, находящегося на расстоянии
![]() от задвижки
от задвижки
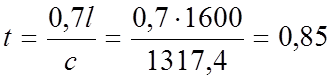 с.
с.
Ответ: ![]() с;
с; ![]() с.
с.
Задача 7.1. В
горизонтальной трубе диаметром ![]() мм (шероховатость
мм (шероховатость
![]() мм) движение воды происходит под
давлением поршня, нагруженного силой
мм) движение воды происходит под
давлением поршня, нагруженного силой ![]() кН, который
перемещается равноускоренно с ускорением
кН, который
перемещается равноускоренно с ускорением ![]() м/с2.
м/с2.
Определить при расходе ![]() л/с
давление жидкости в сечении трубы, отстоящем от поршня на длину
л/с
давление жидкости в сечении трубы, отстоящем от поршня на длину ![]() м?
м?
Задача 7.2. Поршень,
приводимый в движение с постоянным ускорением ![]() м/с2,
перемещает жидкость в трубе, подключенной к открытому резервуару, где уровень
жидкости
м/с2,
перемещает жидкость в трубе, подключенной к открытому резервуару, где уровень
жидкости ![]() м. Диаметр трубы
м. Диаметр трубы ![]() мм.
мм.
Определить давление у поршня в тот момент, когда он
достиг скорости ![]() м/с, находясь на расстоянии
м/с, находясь на расстоянии ![]() м от резервуара.
Принять
м от резервуара.
Принять ![]() ;
; ![]() .
.
Задача 7.3. Скорость
установившегося движения воды в трубе длиной ![]() м
м
![]() м/с, напор
м/с, напор ![]() м.
м.
Найти величину инерционного напора в конце трубы при установившемся движении через 3 секунды с момента открытия задвижки.
Задача 7.4. К
резервуару, заполненному водой, присоединена труба ![]() м;
м;
![]() мм; в конце трубы установлен клапан.
При быстром открытии клапана в трубе возникает неустановившееся движение, при
котором скорость изменяется от
мм; в конце трубы установлен клапан.
При быстром открытии клапана в трубе возникает неустановившееся движение, при
котором скорость изменяется от ![]() (в момент
открытия) до
(в момент
открытия) до ![]() . Напор
. Напор ![]() м.
м.
Определить время, в течение которого скорость в трубе
будет ![]() . Принять значение
. Принять значение ![]() ; местными потерями напора пренебречь.
; местными потерями напора пренебречь.
Задача 7.5. При
каком начальном давлении ![]() воды в стальной
трубе длиной
воды в стальной
трубе длиной ![]() м, диаметром
м, диаметром ![]() мм
и толщиной стенки
мм
и толщиной стенки ![]() мм при прямом гидравлическом
ударе давление
мм при прямом гидравлическом
ударе давление ![]() МПа?
МПа?
Задача 7.6. По
латунной трубке длиной ![]() м, диаметром
м, диаметром ![]() мм и толщиной стенки
мм и толщиной стенки ![]() мм подается масло с расходом
мм подается масло с расходом ![]() л/мин к
распределительному устройству, время срабатывания кото-
л/мин к
распределительному устройству, время срабатывания кото-
 рого
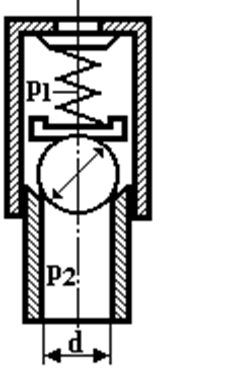
рого ![]() с. Перед распределительным
устройством на трубе установлен предохранительный клапан (рис. 7.1) диаметром
с. Перед распределительным
устройством на трубе установлен предохранительный клапан (рис. 7.1) диаметром ![]() мм. Шарик клапана прижат пружиной с
начальным поджатием пружины
мм. Шарик клапана прижат пружиной с
начальным поджатием пружины ![]() мм. Ход клапана
мм. Ход клапана ![]() мм. Давление за клапаном равно атмосферному.
мм. Давление за клапаном равно атмосферному.
Определить необходимую жесткость пружины. Принять ![]() МПа;
МПа; ![]() МПа;
удельный вес масла
МПа;
удельный вес масла ![]() Н/м3.
Н/м3.
Задача 7.7. В
стальной трубопровод длиной![]() м и внутренним
диаметром
м и внутренним
диаметром ![]() мм из
мм из
Рис. 7.1. К задаче 7.6 гидроцилиндра поступает жидкость с расходом
![]() л/мин. Диаметр
гидроцилиндра
л/мин. Диаметр
гидроцилиндра ![]() мм; нагрузка приложена к
поршню,
мм; нагрузка приложена к
поршню, ![]() кН; жидкость – минеральное масло (
кН; жидкость – минеральное масло (![]() Н/м3,
Н/м3, ![]() Ст).
Ст).
Определить показание манометра, установленного в конце
трубопровода; на сколько изменится это показание при мгновенном перекрытии трубопровода.
Принять ![]() мм;
мм; ![]() МПа;
МПа;
![]() МПа.
МПа.
7.4. Ответы к главе 7
7.1. ![]() МПа. 7.2.
МПа. 7.2. ![]() кПа. 7.3.
кПа. 7.3. ![]() м. 7.4.
м. 7.4. ![]() с. 7.5.
с. 7.5. ![]() МПа. 7.6.
МПа. 7.6. ![]() Н/мм. 7.7.
Н/мм. 7.7. ![]() МПа;
МПа; ![]() МПа.
МПа.
8. ГИДРОМАШИНЫ
7.1. Основные положения
Понятие «гидромашины» включает в себя насосы и гидродвигатели. В насосе происходит преобразование энергии приводящего двигателя в энергию потока жидкости, а гидродвигатель преобразует энергию потока жидкости в механическую работу.
Наибольшее распространение получили объемные и лопастные насосы и гидродвигатели. Объемные гидромашины работают за счет изменения объема рабочих камер, периодически соединяющихся с входным и выходным патрубками. Рабочим органом лопастной машины является вращающееся рабочее колесо, снабженное лопастями. Энергия от рабочего колеса жидкости (лопастной насос) или от жидкости рабочему колесу (лопастной двигатель) передается путем непрерывного динамического взаимодействия лопастей колеса с обтекающей их жидкостью.
Лопастные насосы. К лопастным насосам относятся центробежные, осевые и диагональные
насосы. Основными рабочими параметрами этих насосов являются:
производительность ![]() , развиваемый напор
, развиваемый напор ![]() , мощность
, мощность ![]() и
коэффициент полезного действия
и
коэффициент полезного действия ![]() .
.
Теоретическая производительность насоса равна
![]() ,
,
где ![]() -
наружный диаметр рабочего колеса;
-
наружный диаметр рабочего колеса; ![]() - ширина рабочего
колеса на выходе;
- ширина рабочего
колеса на выходе; ![]() - радиальная составляющая
абсолютной скорости на выходе.
- радиальная составляющая
абсолютной скорости на выходе.
Фактическая
производительность насоса ![]() меньше
теоретической на величину объемных потерь (утечек), учитываемых объемным коэффициентом
полезного действия
меньше
теоретической на величину объемных потерь (утечек), учитываемых объемным коэффициентом
полезного действия ![]() :
: ![]() .
.
Теоретическая величина напора определяется по зависимости
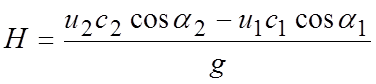 ,
,
где ![]() и
и
![]() - переносная скорость соответственно
на входе и на выходе жидкости из рабочего колеса;
- переносная скорость соответственно
на входе и на выходе жидкости из рабочего колеса; ![]() и
и
![]() - абсолютная скорость соответственно
на входе и на выходе из рабочего колеса;
- абсолютная скорость соответственно
на входе и на выходе из рабочего колеса; ![]() и
и
![]() - углы соответствующих треугольников
скоростей.
- углы соответствующих треугольников
скоростей.
Фактический
напор насоса ![]() меньше теоретического на величину
гидравлических потерь, учитываемых гидравлическим коэффициентом полезного
действия
меньше теоретического на величину
гидравлических потерь, учитываемых гидравлическим коэффициентом полезного
действия ![]() :
: ![]() .
.
Полезная мощность насоса равна
![]() ,
,
где ![]() -
удельный вес жидкости.
-
удельный вес жидкости.
Потребляемая
мощность ![]() больше полезной на величину потерь в
насосе. Эти потери оцениваются коэффициентом полезного действия насоса
больше полезной на величину потерь в
насосе. Эти потери оцениваются коэффициентом полезного действия насоса ![]()
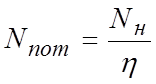 .
.
Полный коэффициент полезного действия насоса равен
![]() .
.
Формулы
пересчета основных рабочих параметров для одного и того же насоса, работающего
на разных частотах вращения (при условии ![]() )
принимают вид:
)
принимают вид:
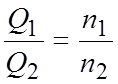 ;
; 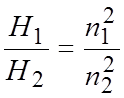 ;
; 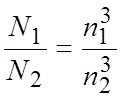 .
.
Для
сравнительной оценки различных типов колес насосов служит коэффициент
быстроходности ![]() (об/мин)
(об/мин)
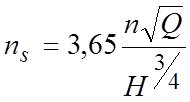 .
.
Значения ![]() для соответствующих типов колес
приведены в Приложении 8.
для соответствующих типов колес
приведены в Приложении 8.
Допустимая
высота всасывания ![]() (рис. 8.1) насосов
рассчитывается из условия бескавитационного режима работы
(рис. 8.1) насосов
рассчитывается из условия бескавитационного режима работы
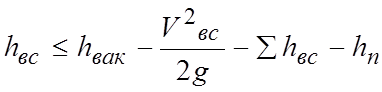 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.