Изучение относительного покоя жидкости во вращающемся сосуде: Методические указания к лабораторной работе

Министерство образования Российской Федерации

ГОУВПО

“Комсомольский-на-Амуре государственный технический университет”

Кафедра “Кораблестроение”

ИЗУЧЕНИЕ ОТНОСИТЕЛЬНОГО ПОКОЯ ЖИДКОСТИ ВО ВРАЩАЮЩЕМСЯ СОСУДЕ

Методические указания к лабораторной работе по курсам

“Гидравлика, гидромашины и гидропривод”,

“Прикладная механика жидкости и газов”,

“Гидравлика и гидромашины”,

“Гидрогазодинамика”

Комсомольск-на-Амуре 2003

УДК 621.225

Изучение относительного покоя жидкости во вращающемся сосуде / Сост. А.В.Космынин, И.В.Каменских – Комсомольск-на-Амуре:

«Комсомольский-на-Амуре гос. тех. ун-т», 2003. - 6 с.

Представлены основные выражения для расчета параметров формы свободной поверхности жидкости во вращающемся сосуде. Описаны лабораторная установка и методика обработки данных.

Методические указания рекомендуются для студентов специальностей 330100, 230300, 552600, 140200, 120300, 120500, 120100, 290500, 170500, 551800, 130100.

Печатается по постановлению редакционно-издательского совета ГОУВПО «Комсомольский-на-Амуре государственный технический университет».

Согласовано с отделом стандартизации и метрологии.

Рецензент В.С. Виноградов

Цель работы: построить линию свободной поверхности в координатах x-z, сравнить линию построенную на основании опыта, с полученной аналитическим путем.

3

 

1 ОБЩИЕ ПОЛОЖЕНИЯ

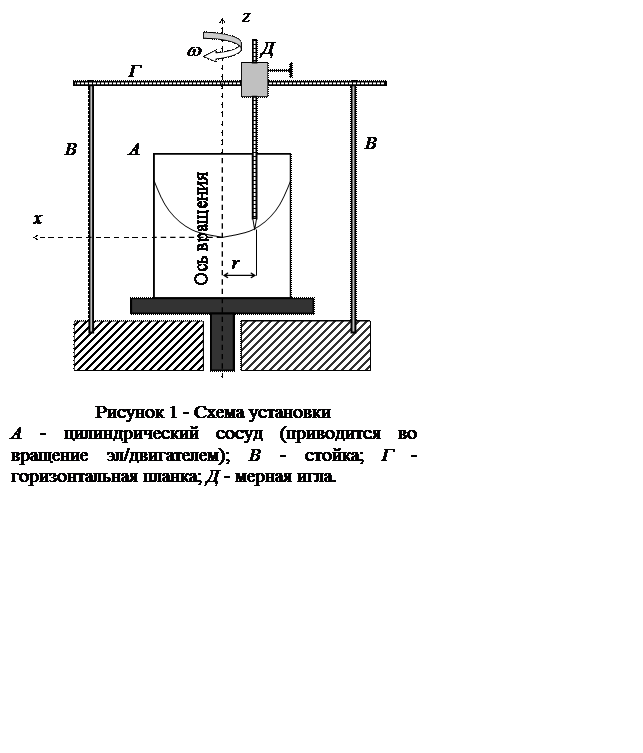
Вертикальный цилиндрический сосуд (см. рисунок 1), наполненный капельной жидкостью, вращается вокруг своей вертикальной оси с постоянной угловой скоростью w. Заключенная в нем жидкость, вследствие ее вязкости увлекаемая сосудом, вращается вместе с ним с той же угловой скоростью и, следовательно, находится в покое относительно сосуда. Требуется построить свободную поверхность жидкости во вращающемся сосуде, пользуясь теоретическими и опытными данными, и сравнить полученные результаты.

Для определения аналитическим способом формы свободной поверхности жидкости  во вращающемся сосуде воспользуемся дифференциальным уравнением поверхностей равного давления, справедливым в случае покоя жидкости (абсолютного или отно­сительного) и имеющим вид

,                                     (1)

где X, Y, Z- проекции на соответствующие оси координат объемных сил, действующих на жидкость и отнесенных к единице массы ее; dx, dy, dz– произвольные приращения координат.

В рассматриваемом нами случае относительного покоя жидкости на нее действуют объемные силы:

1.  Сила тяжести, направленная вертикально вниз: величина ее в любой точке равна массе жидкости m сосредоточенной в этой точке, умноженной на ускорение силы тяжести g.

2.  Центробежная сипа инерции, направленная по радиусу цилиндра от оси вращения; величина ее в некоторой точке, находящейся на расстоянии r от этой оси, для массы жидкости m, сосредоточенной в данной точке, равна .

Взяв начало координат в точке О пересечения свободной поверхности с осью вращения сосуда и направив оси координат, как показано на рисунке 1, получим следующие значения.

;

;

.

Подставляя эти значения X, Y, Zв уравнение (1), получим

4

.

Интегрируя это уравнение имеем:

,

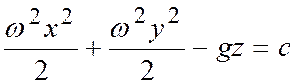откуда

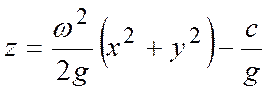.                                 (2)

В рассматриваемом случае относительного покоя капельной жидкости полученное уравнение (2) является уравнением поверхностей равного давления, образующих семейство параболоидов вращения вокруг оси.

Постоянную интегрирования для свободной поверхности жидкости, также являющейся поверхностью равного давления, определим из того условия, что для нее при x=y=0 и z=0.

Тогда получим, что С=0.

Подставляя это значение С в уравнение (2) и имея в виду, что , получим в выбранной системе координат следующее уравнение свободной поверхности жидкости во вращающемся сосуде:

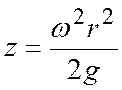.                                                           (3)

Пользуясь этим уравнением при заданной угловой скорости вращения сосуда  (n – частота вращения вала, мин^-1), легко построить свободную поверхность жидкости в нем.

Определение формы свободной поверхности жидкости во вращающемся сосуде производится с помощью специального прибора (см. рисунок 1).

2 ВЫПОЛНЕНИЕ ОПЫТА

Для проведения опыта по определению формы свободной поверхности жидкости во вращающемся сосуде сначала определяют величину угловой скорости его вращения и после того, как установится покой жидкости относительно сосуда, с помощью мерной иглы измеряют расстояние по вертикали от планки Г до свободной поверхности жидкости в различных точках, находящихся в момент измерения в плоскости диаметрального сечения сосуда, параллельной планке Г. Измерив такие расстояния при разных значениях радиуса r, определяемого по делениям планки Г, по точкам строят искомую свободную поверхность жидкости во вращающемся сосуде и сравнивают ее со свободной поверхностью, найденной на основании теоретических вычислений по уравнению (3), при тех же, что и в опытах, значениях w и r.

		5

 

Это дает возможность выяснить, в какой мере результаты теоретических вычислений подтверждаются опытами.

Все результаты опытных наблюдений, измерений и необходимых вычислений сводятся в таблицу 1.

Таблица 1 – Результаты

n/n	Отчет по мерной игле в см, r	z, см		Погрешность
		Опытные значения	Теоретические значения

6

Поданным таблицы необходимо построить две свободные поверхности жидкости во вращающемся сосуде; одна - соответствующая теоретическим вычислениям, а другая - опытным данным.

3 ТРЕБОВАНИЯ К ОТЧЕТУ

Отчет по работе должен содержать:

·  схему установки и ее краткое описание;

·  основные теоретические положения;

·  таблицу опытных данных;

·  графическое изображение линии свободной поверхности, полученной на основании опыта и аналитическим путем;

·  краткие выводы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.  Башта Т.М. и др., Гидравлика, гидравлические машины и гидравлические приводы, 1982. – 423 с.

2.  Задачник по машиностроительной гидравлике /Под ред. И.И. Куколевского и Л.Г. Подвидза. – М.: Машиностроение, 1981. – 464 с.