Центр параллельных сил

Лекция 12

7. ЦЕНТР  ПАРАЛЛЕЛЬНЫХ  СИЛ

          Пусть на абсолютное твердое тело действует пространственная система параллельных сил  направленных в одну сторону (рис.7.1).

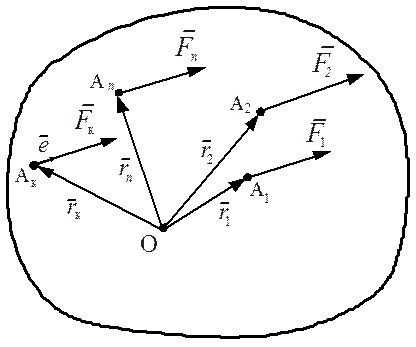
Рис. 7.1

Упростим эту систему сил, приведя ее к произвольному центру О, причем точка приложения к-ой силы  определяется относительно неподвижного центра О радиусом-вектором  (к = 1, 2, …, n).

Согласно теореме Пуансо данная система сил  эквивалентна одной силе 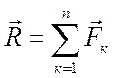, приложенной в центре О, и паре сил с моментом

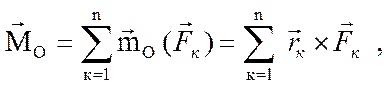                          (7.1)

Так как все силы  параллельны друг другу и направлены в одну сторону, то главный вектор  параллелен любой силе  и его модуль равен арифметической сумме модулей действующих сил

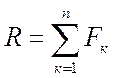,                                                        (7.2)

где  − модуль к-ой силы.

Главный момент системы сил относительно центра О 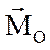 будет перпендикулярен главному вектору , поскольку он равен геометрической сумме коллинеарных векторов 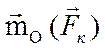, каждый из которых перпендикулярен вектору соответствующей силы , т.е. перпендикулярен вектору (рис. 7.2).

                   

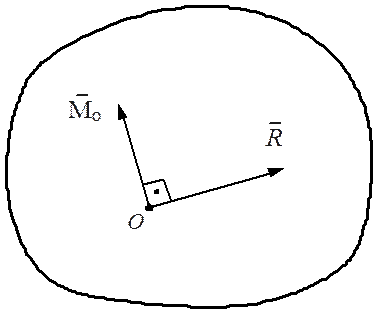
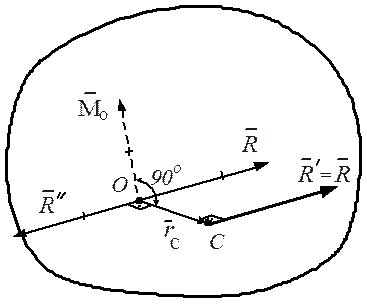
Рис. 7.2                                                          Рис.7.3

Заменим главный момент 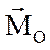 парой сил , , лежащих в перпендикулярной ему плоскости, такой, что , а  (рис. 7.3).

При этом

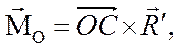
или

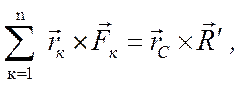                                     (7.3)

где  радиус-вектор точки С.

Фактически формула (7.3) выражает теорему Вариньона (3.20) для системы сил . Но силы  и образует уравновешенную систему сил, которая согласно аксиоме 2 статики может быть отброшена.

Следовательно, любая система параллельных сил  эквивалентна одной силе () являющейся их равнодействующей, приложенной в точке С.

Очевидно, что если повернуть параллельные силы  около точек их приложения  в одну и ту же сторону на один и тот же угол, то их равнодействующая  повернется в точке С в ту же сторону на тот же угол.

Точка С, через которую проходит линия действия равнодействующей системы параллельных сил, при любых поворотах этих сил около точек их приложения в одну и ту же сторону на один и тот же угол, называется центром параллельных сил.

Для определения положения точки С введем единичный вектор  () по направлению к-ой силы . Тогда

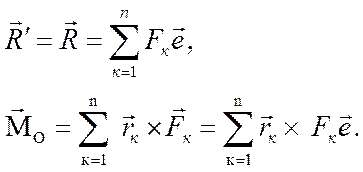                             (7.4)

С учетом (7.4) формула (7.3) принимает вид

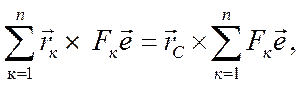
или

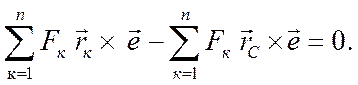
Отсюда получаем

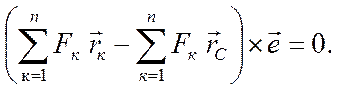                                 (7.5)

Поскольку векторное произведение  в (7.5) равно нулю при произвольном направлении единичного вектора , то формула (7.5) имеет место, если вектор

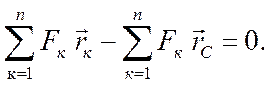
Отсюда определяем радиус-вектор  центра С параллельных сил:

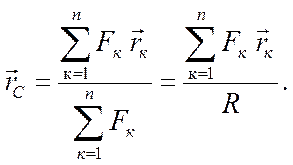                                       (7.6)

Отметим, что все полученные выше формулы будут справедливы для системы параллельных сил, направленных в противоположные стороны, если   считать алгебраическими величинами (>0, если сила  параллельна единичному вектору  и <0, если сила  направлена противоположно ), и .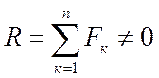

ЦЕНТР   ТЯЖЕСТИ   ТВЕРДОГО   ТЕЛА

Вблизи поверхности Земли на каждую материальную частицу тела действует сила тяжести (сила притяжения) направленная к центру Земли. Так как размеры тела малы по сравнению с радиусом Земли, то силы тяжести частиц тела  можно считать параллельными друг другу и постоянными по модулю для каждой частицы тела при любых его поворотах  (рис. 7.4).

Рис. 7.4

Равнодействующая сил тяжести  частиц тела называется весом тела , модуль которой определяется согласно (7.2)

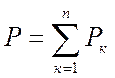.                                                      (7.7)

Центром тяжести твердого тела называется геометрическая точка С, являющаяся центром параллельных сил тяжести , действующих на частицы тела при любых поворотах тела в пространстве.

Согласно (7.6) положение центра тяжести С тела определяется радиусом-вектором

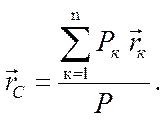                                               (7.8)

Тогда декартовые координаты точки С находится по формулам:

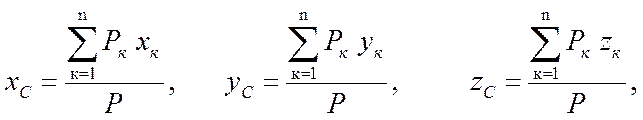                    (7.9)

где  декартовые координаты точек приложения сил тяжести , действующие на частицы тела.

Для однородного тела объема вес  любой его части объема

,                                                       (7.10)

где  вес единицы объема, а вес всего тела

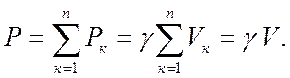                                        (7.11)

Подставив (7.10) и (7.11) в (7.9), получим координаты центра тяжести однородного тела

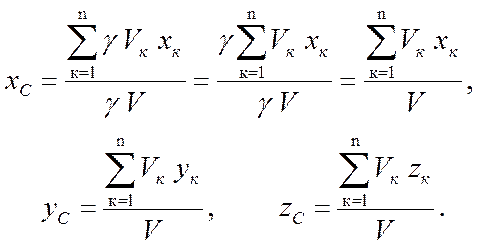                    (7.12)

Поскольку положение центра тяжести С однородного тела не зависит от объемной плотности вещества , а определяется только геометрической формой тела, поэтому точка С называется центром тяжести объема .

Проводя аналогичные рассуждения для однородной плоской пластины площади 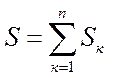, получим ее координаты центра тяжести С:

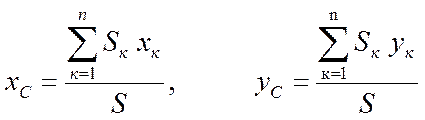,                                        (7.13)

где  координаты к-ой части пластины площади . Формулы (7.13) определяют координаты центра тяжести площади S.

Так же можно найти координаты центра тяжести линии длиной L:

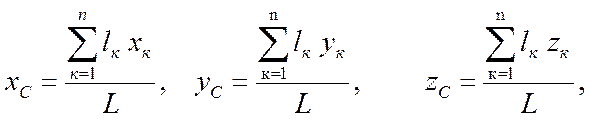                 (7.14)

где  длина к-ой части линии.

Рассмотрим некоторые способы определения координат центров тяжести однородных тел.

1. Способ симметрии. Если однородное тело имеет плоскость, ось или центр симметрии, то центр тяжести С лежит соответственно в плоскости, на оси или в центре симметрии тела.

2. Способ разбиения. Если однородное тело можно разбить на конечное число частей, положения центров тяжести, которых известны, то координаты центра тяжести всего тела можно определить применением формул (7.12) – (7.14), где n соответствует числу частей, на которые разбивается тело.

3. Способ дополнения. Этот способ применяется к телам, имеющим вырезы, когда данное тело можно представить как разность тел. Причем положения центра тяжести тела без выреза и вырезанной части должны быть известны. В этом случае объем (площадь) тела без выреза считается положительным, а объем (площадь) вырезанной части отрицательным.

4. Способ интегрирования. Если тело нельзя разбить на конечное число частей, положения центров тяжести, которых известны, то его разбивают на бесконечное число элементарных объемов (площадей, линий). Координаты центров тяжести тел можно получить с помощью формул (7.12) - (7.14), в которых суммы переходят в соответствующие интегралы.

Приведем без доказательств координаты центров тяжести некоторых однородных тел.

Рис. 7.5

1. Центр тяжести С площади треугольника (рис. 7.5а) лежит в точке пересечения его медиан, причем тока С делит каждую медиану в отношении 2:1 (рис.7.5), т.е.

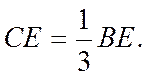                                                  (7.15)

2. Центр тяжести С дуги окружности радиусом R с центральным углом  (рис.7.5б) лежит на оси ее симметрии, на расстоянии от центра О равном

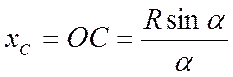,                                     (7.16)

где a - в радианах.

3. Центр тяжести С площади кругового сектора радиусом R с центральным углом  (рис.7.5в) лежит на оси его симметрии на расстоянии от центра О равном

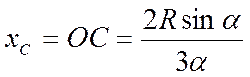.                                  (7.17)

4. Центр тяжести С объема конуса (рис. 7.6а) (призмы) лежит на отрезке прямой ЕС₁, соединяющей вершину Е конуса с центром тяжести С₁ его основания, причем

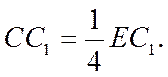                                               (7.18)

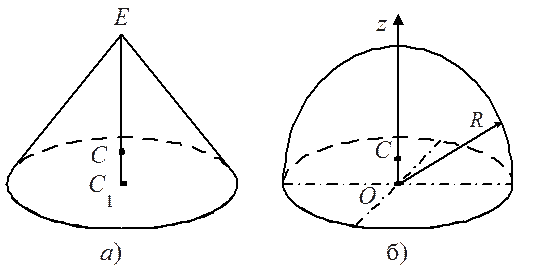
Рис. 7.6

5. Центр тяжести С объема полушара радиусом R (рис.7.6б) лежит на оси симметрии Оz с координатой

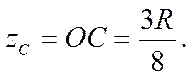                                 (7.19)

Пример 7.1Определить координаты центра тяжести С контура ОАВD, состоящую из прямолинейных отрезков ОА, ОВ и дуги АВ окружности радиуса R = 10 см (рис. 7.7).

Решение. Прямая у = х является осью симметрии контура ОАВD, поэтому его центр тяжести С лежит на этой прямой.

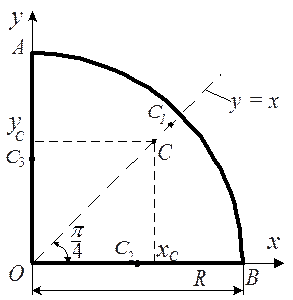
Рис. 7.7

Следовательно,

.                                                        (7.20)

Разобьем контур ОАВD на три элемента, для каждого из которых находим его длину  икоординату  его центра тяжести С_к (к = 1, 2, 3) (см. рис. 7.7):

1) для дуги АВ радиусом Rс центральным углом 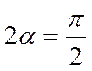 длина дуги

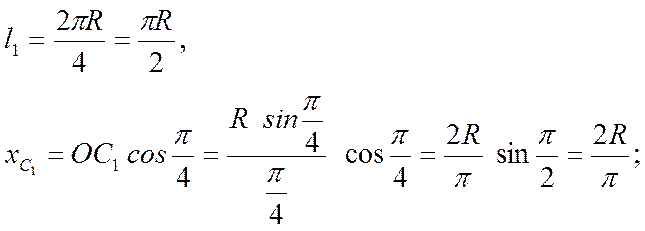
2) для отрезка ОВ его длина  ,   

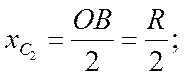
3) для отрезка ОА его длина  ,   

Для определения координаты  центра тяжести С контура ОАВD подставим в формулу (7.14) найденные величины, получим

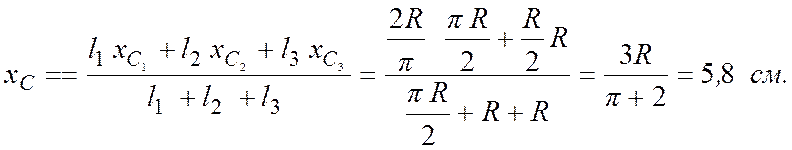
Следовательно, координаты центра тяжести С контура ОАВDсм.

Пример 7.2. Из однородной пластины в виде прямоугольного треугольника ОАВ с основанием ОВ и высотой ОА вырезан полукруг радиусом R(рис. 10.8).           Определить координаты центра тяжести С оставшейся заштрихованной части треугольника.Решить задачу при следующих данных: ОВ = 60 см,    ОА = 45 см,     R = 20 см.

Решение. Примем вершину О треугольника ОАВ за начало декартовой системы координат Оху. Пластину рассматриваем как фигуру, составленную из двух частей: треугольника ОАВ с центром тяжести С₁ в точке пересечения его медиан; и выреза в виде полукруга радиусом R = 20 см, с центральным углом  с центром тяжести С₂ , лежащим на оси его симметрии параллельной оси Оу (рис. 7.8).

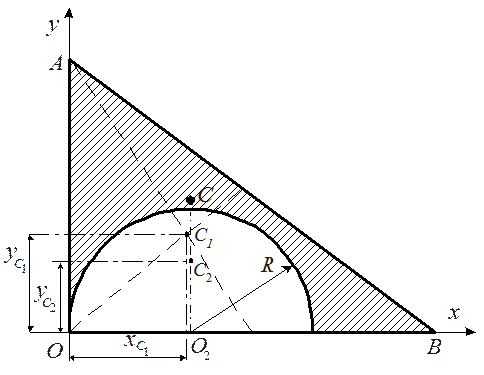
Рис. 7.8

Вычислим площади S₁, S₂ и координаты центров тяжести С₁ и С₂ частей пластины, подставляя данные задачи:

1)  площадь треугольника ОАВ

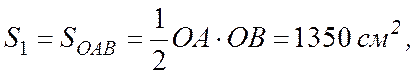
согласно (7.15)

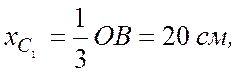
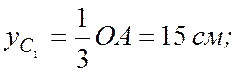
2)  площадь полукруга радиусом R = 20 см отрицательна, так как она вычитается из площади треугольника ОАВ

,

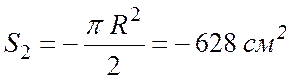с учетом формулы (7.17) вычисляем координату

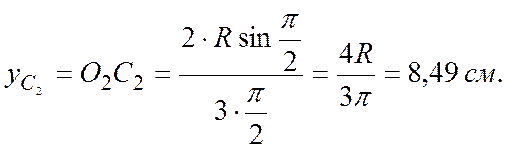
Площадь S всей пластины

Координаты центра тяжести С треугольника из которого  вырезан полукруг находим по формулам (7.13), подставляя найденные выше величины:

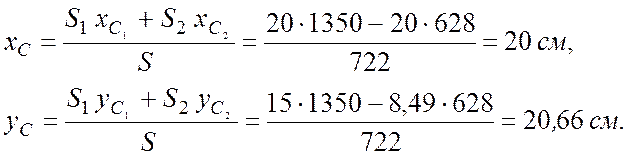
Покажем положение центра тяжести С на рис. 7.8.

Следовательно, координаты центра тяжести С заштрихованной части треугольника    .

Вопросы для самопроверки

1. Чем заменяется любая система параллельных сил?

2. Какой формулой определяется радиус-вектор  центра С параллельных сил?

3. Что называется весом тела?

          4. Что называется центром тяжести твердого тела?

          5. По каким формулам вычисляются координаты центра тяжести однородной плоской платины площади S?

          6. Какие существуют способы для вычисления координат центров тяжести однородных тел?