Дифференциальные уравнения движения твердого тела

Лекция 19

7. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ

ТВЕРДОГО ТЕЛА

Применим общие теоремы динамики к получению дифференциальных уравнений движения твердого тела. Рассмотрим простейшие случаи движения твердого тела.

1. Поступательное движение твердого тела. Из теоремы о движении центра масс (3.13) имеем

.

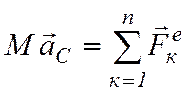Однако при поступательном движении ускорения всех точек тела геометрически равны, т.е. , где 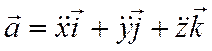 - ускорение произвольной точки тела. Тогда (3.13) принимает вид:

,

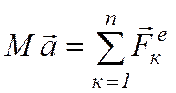или в проекции на координатные оси получаем

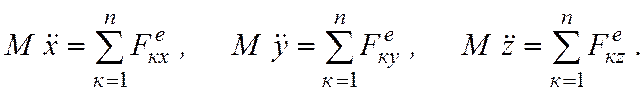          (7.1)

Уравнения (17.1) называются дифференциальными уравнениями поступательного движения твердого тела в декартовых координатах.

2. Вращательное движение твердого тела. Рассмотрим твердое тело, вращающееся вокруг неподвижной оси z, под действием сил 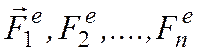 (рис. 17.1). Кроме этих сил на тело действуют реакции  подпятника А и  подшипника В. Воспользуемся теоремой об изменении кинетического момента системы относительно оси вращения z (6.15):

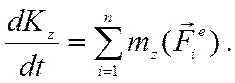                                     (7.2)

В правой части (17.2) отсутствуют моменты реакций  и , так как они равны нулю (реакции  и  пересекают ось z). Согласно (6.9) для вращающегося тела , где для твердого тела . Подставляя в (7.2), находим

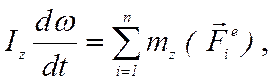                                (7.3)

или, поскольку 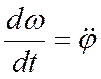, получаем

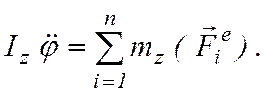                                           (7.4)

Уравнение (7.4) называется дифференциальным уравнением вращательного движения твердого тела.

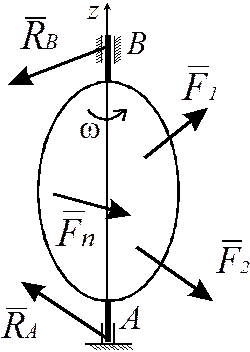
Рис. 7.1

Иногда вводится обозначение 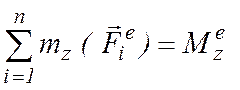, и величина  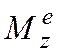называется вращающим моментом. Тогда, так как  - угловое ускорение тела, то (7.4) принимает вид

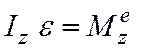,                                                 (7.5)

т.е. произведение момента инерции тела относительно оси вращения на угловое ускорение равно вращающему моменту. Из сравнения (7.5) с основным законом динамики (1.1) модно заключить, что момент инерции тела относительно оси его вращения играет такую же роль, как и масса точки при ее движении. Следовательно,  является мерой инертности тела при вращательном движении.

Из уравнения (7.4) можно:

1)  зная закон вращения , найти ;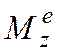

2) зная вращающий момент , определить закон вращательного движения тела вокруг неподвижной оси , т.е. решить основную задачу динамики для твердого тела. В частности,

1. если 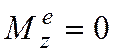, то , и тело вращается равномерно по закону (2.9) ;

2. если , то , и тело совершает равнопеременное вращение по закону (2.11) .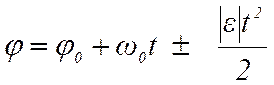

3. Плоскопараллельное движение твердого тела.Пусть свободное тело совершает плоское движение относительно неподвижной плоскости Оху под действием внешних сил 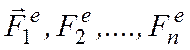 и имеет в данный момент времени угловое ускорение  (рис.7.2). Примем за полюс центр масс С тела. Тогда его движение можно рассматривать как слагающееся из поступательного движения вместе с центром масс С и вращательного движения вокруг оси , перпендикулярной плоскости Оху и движущейся поступательно вместе с подвижной системой отсчета .

Рис. 7.2

Если х_С и у_С - координаты центра масс С в неподвижной системе отсчета Оху, то по теореме о движении центра масс (3.14) получим два дифференциальных уравнения, характеризующих поступательное движение тела вместе с центром масс С:

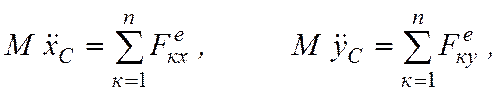
где М - масса тела.

Третье дифференциальное уравнение, определяющее вращательное движение вокруг оси , получаем из (7.4)

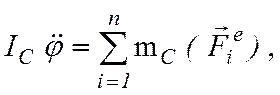
поскольку согласно (6.18) вид теоремы моментов, с помощью которой была получена формула (7.4), не изменится в системе координат , движущейся поступательно с центром масс С тела.

Тогда окончательно находим дифференциальные уравнения плоскопараллельного движения твердого тела:

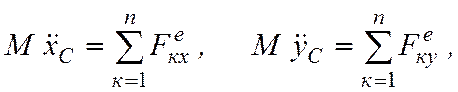
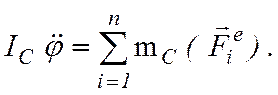          (7.6)

Пример 7.1. Цилиндрический вал массой m и радиусом R вращается с угловой скоростью n_o относительно продольной центральной оси симметрии О (рис. 7.3).

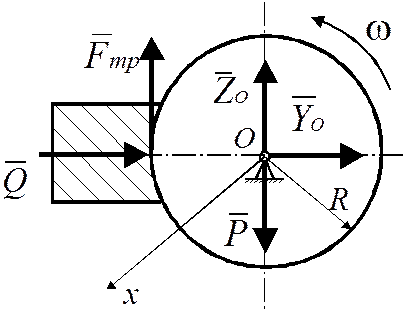
Рис. 7.3

С какой силой  надо прижать тормозную колодку к валу, чтобы остановить его за время t₁ , если коэффициент трения скольжения колодки о вал - f, а радиус инерции вала относительно оси вращения равен . Трением в опорах вала пренебречь. Найти число  полных оборотов вала с момента начала торможения до остановки.

Решить задачу при следующих данных: m = 10 кг;  R= 0,1 м ;   n_o = 600 об/мин;   t₁= 10 с ;   f= 0,4 ;  =0,3 м .

Решение.Направляем ось Ох по оси вращения вала (рис. 7.3). Тогда дифференциальное уравнение вращения вала вокруг неподвижной оси Ох в форме (6.3) имеет вид:

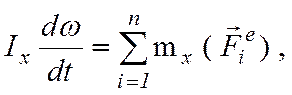                                       (7.7)

где согласно (5.2) .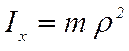

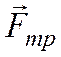К валу приложены внешние силы: силы тяжести , реакции опор , сила  и сила трения скольжения  колодки о вал, направленная в точке контакта по касательной (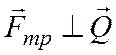) в сторону, противоположную движению, причем . Так как моменты опорных реакций , сил  и  относительно оси вращения Ох равны нулю, то

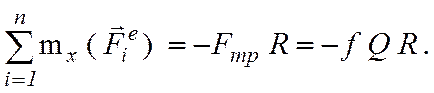                             (7.8)

Момент силы трения 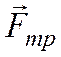 в (7.8) отрицателен, т.к. его направление противоположно направлению  - угловой скорости вращения вала, которое при решении задач по динамике обычно выбирается за положительное.

Тогда с учетом (7.8) дифференциальное уравнение вращения вала принимает вид

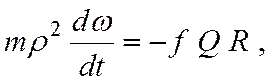
или

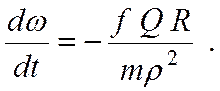                                        (7.9)

Для решения задачи требуется проинтегрировать это уравнение при начальных условиях движения:

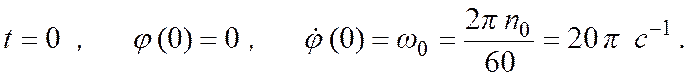             (7.10)

Интегрируя (7.9), находим

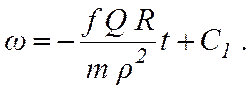                                             (7.11)

Подставив (7.10) в (7.11), определяем постоянную интегрирования . Следовательно, зависимость угловой скорости вращения вала от времени имеет вид

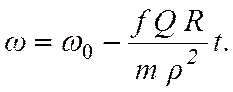                                                (7.12)

Из (7.12) можно определить величину силы , если воспользоваться условием, что в момент времени t = t₁  вал останавливается и его угловая скорость , т.е. получаем

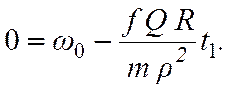
Отсюда с учетом данных задачи находим:

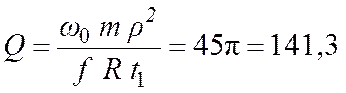Н.

Для определения числа  полных оборотов вала с момента его торможения до остановки запишем (7.12), представив  :

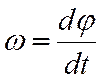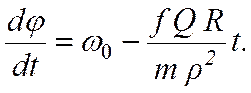                                             (7.13)

Разделяя переменные в (7.13) и интегрируя, получим

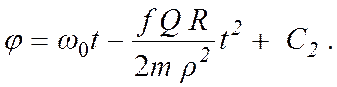
По начальным условиям (7.10) находим . Окончательно определяем закон вращения вала

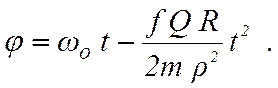                                         (7.14)

Видно, что вал вращается равнозамедленно с угловым замедлением 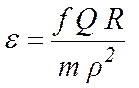. За время t₁  вал, сделав  полных оборотов, повернется на угол . Подставив это условие в (7.14), получим

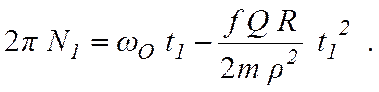
Отсюда находим полное число оборотов вала с момента начала торможения до его остановки

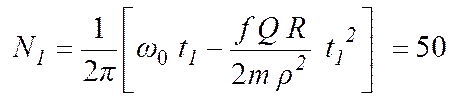об.

Пример 7.2  Тонкий однородный круглый обруч приводится в качение без скольжения по горизонтальной плоскости с помощью горизонтальной силы , численно равной весу обруча . Введя ось Ох в направлении движения обруча и пренебрегая сопротивлением качению, определить закон движения центра масс С обруча, если движение начинается из состояния покоя (рис.7.4).

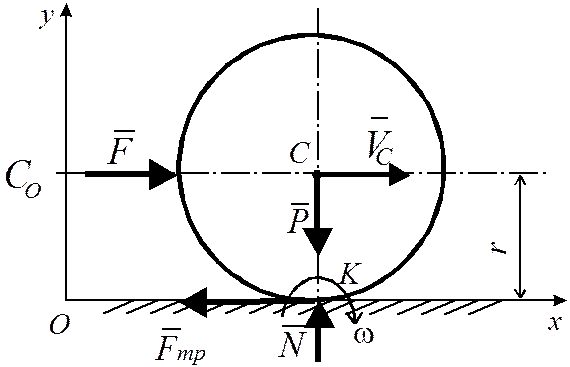
Рис. 7.4

Решение. Обруч совершает плоскопараллельное движение. Начало координат системы Оху поместим в начальный момент времени (см. рис. 7.4). Тогда начальные условия движения имеют вид

.

Угол поворота  обруча отсчитываем в направлении его угловой скорости  - по часовой стрелке.

К обручу приложены внешние силы: сила тяжести , движущая сила , нормальная реакция горизонтальной плоскости  и 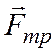 - сила трения обруча о горизонтальную плоскость, направленная в сторону противоположную движению обруча.

Дифференциальные уравнения плоского движения (7.6) для этой задачи имеют вид

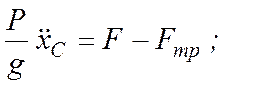
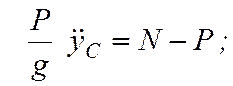                                       (7.15)

гдеr - радиус обруча. При движении обруча , поэтому , и из второго уравнения (6.15) имеем .

Согласно (5.7)

.

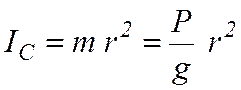При качении обруча без скольжения точка касания К обруча с горизонтальной неподвижной плоскостью является мгновенным центром скоростей. Поэтому

                                           (7.16)

Дифференцируя (7.16) по времени, находим

или

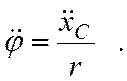                                                     (7.17)

Подставим (7.17) в третье уравнение системы(7.15) и выразим из него силу трения:

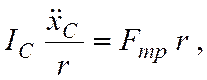
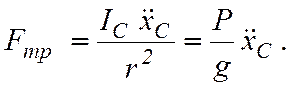                              (7.18)

Тогда с учетом (7.18) запишем первое уравнение системы (7.15)

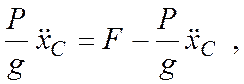
или

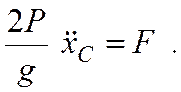                                   (7.19)

Так как по условию  , то дифференциальное уравнение движения центра масс С обруча (7.19) принимает вид:

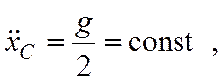                             (7.20)

т.е. центр масс С движется вдоль оси Ох равноускоренно.

Проинтегрируем уравнение (7.20) при нулевых начальных условиях  и получим искомый закон движения центра масс обруча

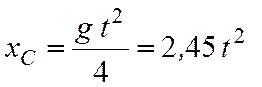м.

Вопросы для самопроверки

1. Влияют ли размеры и форма тела при его поступательном движении?

2. Влияют ли размеры и форма тела при его вращательном движении?

3. При каких условиях тело вращается вокруг оси равнозамедленно?

4. Сколько дифференциальных уравнений движения можно записать для колеса автомобиля движущегося без скольжения на прямолинейном участке пути?