Обобщенные координаты, обобщенные силы

Лекция 24

12. ОБОБЩЕННЫЕ КООРДИНАТЫ, ОБОБЩЕННЫЕ СИЛЫ

Для введения понятия обобщенных координат рассмотрим плоский двойной математический маятник, состоящий из двух невесомых стержней длиной l₁ и l₂ с точечными массами m₁ и m₂ на концах (рис. 12.1). Система обладает двумя степенями свободы.

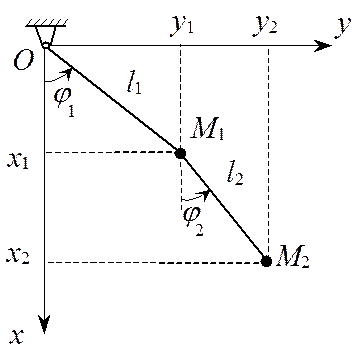
Рис. 12.1

Действительно стержень ОМ₁ может вращаться вокруг неподвижной горизонтальной оси О, перпендикулярной плоскости движения хОу, а стержень M₁M₂ – вокруг горизонтальной оси, проходящей через точку M₁, в той же плоскости. Поэтому уравнения связей имеют вид: z₁=0,z₂=0,

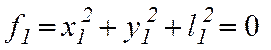
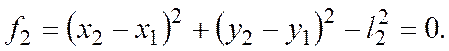
Поэтому, так как n =2, а число уравнений связей k= 4, то S = 3n – k = 2, т.е. лишь две из шести декартовых координат являются независимыми и должны быть заданы. Остальные же координаты можно выразить из уравнений связей через независимые координаты.

На практике координаты х₁, у₁ z₁, х₂, у₂ , z₂ выражают через какие-либо независимые переменные другой природы, в нашем случае ими являются углы  и  отклонения стержней от вертикали:

х₁ = l₁×cosj₁,                     y₁ = l₁×sinj₁,                        z₁=0;

      x₂ = l₁×cosj₁ + l₂×cosj₂,    y₂ = l₁×sinj₁ + l₂×sinj₂ ,        z₂=0.        (12.1)

Здесь углы  и  играют роль независимых параметров, однозначно определяющих положение рассматриваемой механической системы.

Пусть теперь имеется система n материальных точек, на которую наложены k голономных связей, заданных уравнениями (10.2). Поскольку число степеней свободы равно S, то введем независимые переменные           q₁, q₂, ..., q_s. Тогда для рассматриваемой системы соотношения (12.1) примут вид:

x_n = x_n ( q₁, q₂, ..., q_s,,t);

у_n = у_n ( q₁, q₂, ..., q_s ,t);     (n= 1, 2,…, n),

z_n = z_n ( q₁, q₂, ..., q_s ,t);

или

( q₁, q₂, ...,  q_s, t); (n = 1, 2,…, n).                  (12.2)

Отметим, что независимые координаты q_m (m = 1, 2, …, s) – это не обязательно набор Sпеременных из числа декартовых координат x_n, у_n, z_n. Ими могут быть переменные другой природы, так в приведенном выше примере вместо декартовых координат введены угловые координаты.

S независимых параметров  q₁, q₂, ..., q_s однозначно определяющих положение точек материальной системы, совместимое со связями, называются  обобщенными координатами.

Производные от обобщенных координат по времени  называются обобщенными скоростями ( = dq_m /dt).

Размерность обобщенной скорости зависит от размерности обобщенной координаты: если q_m – линейная величина, то  – линейная скорость; если q_m – угол, то  – угловая скорость; если q_m – площадь, то  – секторная скорость. Следовательно, понятие обобщенной скорости охватывает все известные нам понятия о скоростях.

          Для введения понятия обобщенных сил рассмотрим голономную систему, состоящую из nматериальных точек, на которые действуют соответственно силы , , ..., . Пусть система имеет S степеней свободы, и ее положение определяется обобщенными координатами q₁, q₂, ...,q_s. Сообщим системе в фиксированный момент времени такое виртуальное перемещение, при котором обобщенная координата q_m приобретает приращение dq_m> 0, а остальные обобщенные координаты не изменяются. Тогда каждый радиус-вектор  получит виртуальное перемещение ()_m, которое вычисляется как частный дифференциал:

(d)_m = 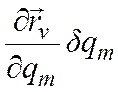.                                              (12.3)

Согласно (10.9) виртуальная работа всех активных сил при вариации dq_m обобщенной координаты q_m запишется в виде:

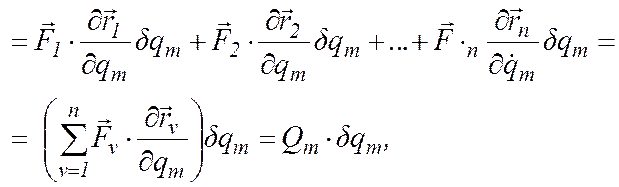
где 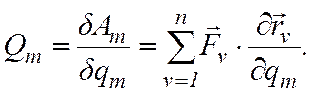                                                                      (12.4)

Величину  называют  обобщенной силой, соответствующей обобщенной координате q_m. Если всем S обобщенным координатам в данный момент времени сообщить положительные приращения (вариации) dq₁, dq₂, ..., dq_s, то полная виртуальная работа всех активных сил в обобщенных координатах

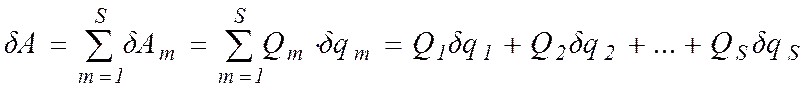.         (12.5)

Из выражения (12.5) следует, что обобщенные силы представляют собой коэффициенты при вариациях обобщенных координат в выражении для виртуальной работы. Проецируя (11.4) на декартовые оси, получим

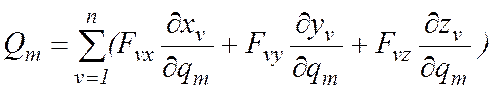.                (12.6)

Если все действующие силы  потенциальные, то их проекции F_nx, F_ny, F_nz на декартовые оси могут быть выражены через потенциальную энергию П системы согласно формулам:

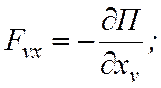
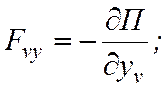
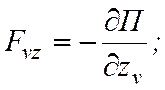                               (22.7)

Подставив (12.7) в (12.6), получим:

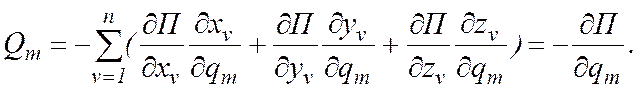
          Для механической системы, находящейся в потенциальном силовом поле, обобщенная сила определяется взятой с обратным знаком частной  производной от потенциальной энергии по соответствующей обобщенной координате:

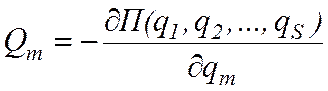.                                 (12.8)

Отметим, что размерность обобщенной силы равна размерности работы, деленной на размерность обобщенной координаты.

Пример 12.1. Определить обобщенную силу математического маятника весом , если длина нити равна l. За обобщенную координату взять угол отклонения j маятника от вертикали (рис. 12.2).

           

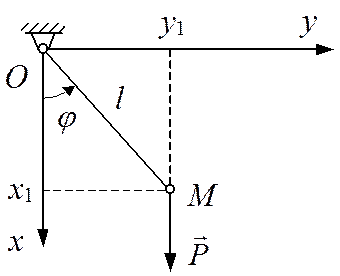
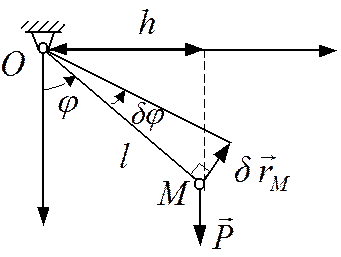
Рис. 12.2                                                   Рис. 12.3

Решение. Математический маятник является системой с одной степенью свободы (S = 1), так как для определения его положения достаточно задать один параметр.

Рассмотрим маятник в произвольном положении. За обобщенную координату q примем угол j. Активной силой, действующей на маятник, является сила тяжести .

Способ 1. Поскольку сила  потенциальна, то для определения обобщенной силы Q воспользуемся формулой (12.8). Для вычисления потенциальной энергии П маятника направим ось х по вертикали вниз, взяв за начало отсчета потенциальной энергии точку Оподвеса маятника, т.е. П(х=0)= 0. Потенциальная энергия маятника равна работе силы тяжести  на перемещении материальной точки из данного положения М в нулевое, т.е. П = –Р×х₁ = –Р×l×cosj. Согласно (12.8)

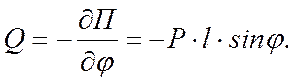
Способ 2. Наиболее распространен-ным методом вычисления обобщенной силы является её определение  по формуле (11.4)  Q_m = dA_m/dq_m. Сообщим маятнику в данный момент времени виртуальное перемещение dj> 0, т.е. в сторону возрастания угла j (рис. 12.3), и вычислим элементарную работу силы тяжести  на этом перемещении:

dA= – P×h×dj,

где h = l×sinj, – плечо силы  относительно центра вращения точки O. Следовательно,