dA = – P×l×sinj×dj.
Тогда
Q= dA/dj = – P×l×sinj.
ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИЙ
В ОБОБЩЕННЫХ КООРДИНАТАХ
Согласно принципу виртуальных перемещений (10.12), необходимым и достаточным условием равновесия голономной материальной системы, подчиненной идеальным связям, является равенство нулю виртуальной работы действующих активных сил, dA = 0. В обобщенных координатах для системы с S степенями свободы это условие с учетом (12.5) принимает вид
Q1dq1 + Q2dq2 +…+ Qsdqs = 0. (12.9)
Поскольку dq1, dq2, ..., dqs – независимые вариации обобщенных координат, то выражение (12.9) выполняется только тогда, когда все обобщенные силы одновременно равны нулю, т.е.
Q1 = 0, Q2 = 0, …, Qs = 0. (12.10)
Уравнения (12.10) выражают принцип виртуальных перемещений в обобщенных координатах: для равновесия материальной системы необходимо и достаточно, чтобы все обобщенные силы, соответствующие выбранным для системы обобщенным координатам, были равны нулю.
Если
обобщенные силы зависят не только от обобщенных координат, но и от обобщенных
скоростей 
, 
, ..., 
, то в (12.10) все обобщенные скорости нужно приравнять
нулю. Из (12.10) следует, что количество уравнений равновесия равно числу
обобщенных координат, т.е. числу S степеней свободы системы.
Для консервативной системы условия равновесия (12.10) имеют вид
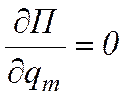(m = 1, 2, …, s). (12.11)
Полный дифференциал потенциальной энергии П(q1, q2, ..., qs) системы определяется выражением
dП(q1, q2, ..., qs) =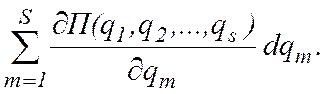 
Следовательно, с учетом (12.11)
dП(q1, q2, ..., qs) =0. (12.12)
Условие
(12.12) означает, что в положении равновесия потенциальная энергия
консервативной системы принимает экстремальное значение. Следовательно,
решения системы уравнений (12.11) – (12.12)
определяют обобщенные координаты, 
соответствующие
положению равновесия системы.
Положение
равновесия материальной системы может быть устойчивым и неустойчивым.
Например, математический маятник (см. рис. 12.2) имеет два положения
равновесия: согласно (12.10) Q =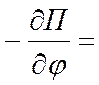
– P×l×sinj = 0, если 
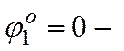нижнее положение равновесия; и 
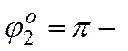верхнее положение равновесия. Очевидно,
что верхнее положение равновесия маятника практически нельзя осуществить, оно
является неустойчивым; нижнее положение легко реализуемо, это устойчивое
положение равновесия.
Достаточные условия устойчивости положения равновесия для консервативной системы определяет теорема Лагранжа−Дирихле: если в положении изолированного равновесия консервативной системы с идеальными стационарными связями потенциальная энергия имеет минимум, то это положение равновесия устойчиво.
По теореме Лагранжа-Дирихле, для доказательства устойчивости равновесия консервативной системы достаточно убедиться в том, что потенциальная энергия в рассматриваемом положении минимальна. Для системы с одной степенью свободы минимум определяется тривиально: достаточно убедиться, что вторая производная от потенциальной энергии по обобщенной координате q, вычисленная в положении равновесия, положительна, т. е.
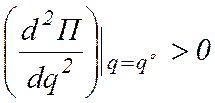. (12.13)
В
частности для рассмотренного выше математического маятника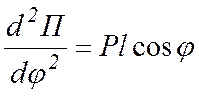 
, и
для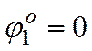 
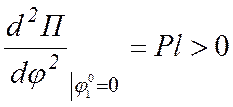, т.е. по теореме Лагранжа-Дирихле
это состояние устойчивого равновесия маятника, а для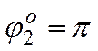 
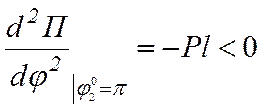, что
соответствует состоянию неустойчивого равновесия.
Пример 12.2 Однородная квадратная пластина может вращаться в вертикальной плоскости около оси, проходящей через точку O, вес пластины равен P, длина ее стороны a (рис. 12.4).
К углу A пластины привязана нить длины l, перекинутая через малый блок B, отстоящий на расстоянии a по вертикали от точки O.
Рис. 12.4
На
нити весит груз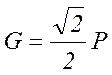 
. Определить положения равновесия системы и
исследовать их устойчивость.
Решение. Рассмотрим равновесие системы, состоящей из однородной квадратной пластины и груза, находящихся в однородном поле сил тяжести. Система имеет одну степень свободы, поэтому за обобщенную координату примем угол y, образованный стороной OA пластины с вертикалью. За начало координат берем точку O, направив ось Z вверх, ось X вправо. Потенциальную энергию П будем отсчитывать от положения Z = 0 , т. е.
П(Z = 0) = 0.
На систему действует сила тяжести 
пластинки,
приложенная в ее геометрическом центре C и сила тяжести груза 
. Поэтому потенциальная энергия системы
П = PZ1 + GZ2,
где Z1 и Z2 – соответствующие координаты точки C и груза G. Выразим Z1 и Z2 через обобщенную координату y:
Z1 = 
(cos y – sin y); Z2= a – l + 2a×sin 
.
Тогда
П
= 
P×a
(cos y – sin y) + G (a – l + 2a×sin ).
или, поскольку G
= 
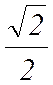P,
П
= 
[a (cos y – sin y) + 
(a – l + 2a×sin )].
Для определения положений равновесия находим производную от потенциальной энергии по обобщенной координате и приравниваем ее нулю:
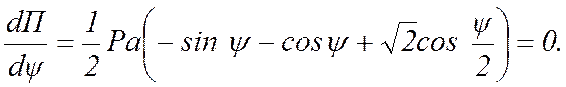
Из этого уравнения получим:
sin y + cos y = cos 
.
Возводим обе части уравнения в квадрат:
sin2 y +2sin y cos y +cos2 y = 2 cos2 ,
так
как sin2y + cos2y =1, а
2cos2 
= 1 + cos y, то
получим
2×sin y×cos y = cos y
или
cosy (2×siny – 1) = 0.
Равновесие возможно, если cos y = 0 или sin y = 1/2, т. е. при четырех значениях угла y :
y1 = p/2, y2 = 3p/2, y3 = p/6, y4 = 5p/6.
Для определения устойчивости каждого из этих положений находим вторую производную от потенциальной энергии по обобщенной координате:
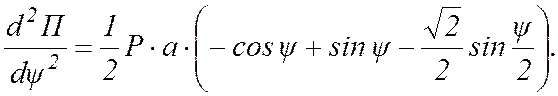
Определим величину и знак этой производной для четырех значений угла:
1)
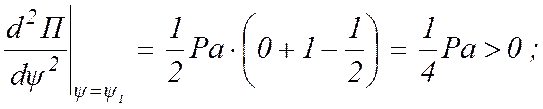
2)
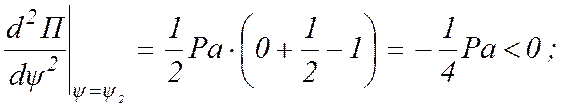
3)
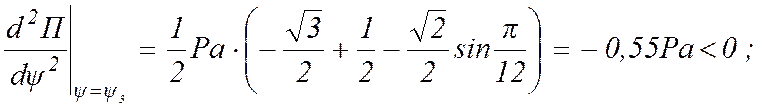
4)
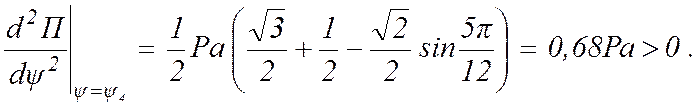
Следовательно, согласно (12.13), положение равновесия
системы устойчиво пр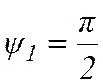и 
и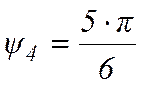 
, но неустойчиво пр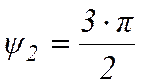и 
и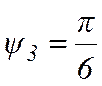 
.
Вопросы для самопроверки
1. Сколько степеней свободы имеет футбольный мяч, находящийся в свободном полете?
2. Материальная система имеет одну степень свободы. Однозначен ли для нее выбор обобщенной координаты?
3. Как определяется обобщенная сила для материальной системы с одной степенью свободы, находящейся под действием только потенциальных сил?
4. От чего зависит размерность обобщенной силы?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.