Рис. 1.10. Иерархическая модель пространственной подсистемы ЭС: K, V, B, U, R – соответственно, множество комплексов, устройств, блоков, узлов и радиоэлементов
Такая иерархическая модель ЭС обладает следующими отличительными особенностями:
1. На самом верхнем уровне модели располагается элемент, представляющий оценку состояния в целом, а на самом нижнем уровне модели располагается максимальное количество элементов, каждый из которых также характеризуется определенным уровнем состояния. Состояние всей ЭС однозначно определяется состояниями ее структурных единиц;
2. Каждая подсистема модели содержит совокупность значений параметров, характерных для нее. Множество значений параметров всех подсистем образуют их семейство, характерное для всей ЭС;
3. Отношения взаимосвязей в таких моделях проявляются между параметрами всех структурных ее уровней, как по горизонтали, так и по вертикали. При этом величины взаимосвязей между параметрами определяются корреляционными или ковариационными матрицами в зависимости от линейных или нелинейных отношений, проявляющихся между ними в составе структурных уровней;
4. Для оценки состояния электронной системы необходима уверенная математическая модель, адекватно описывающая иерархическую ее структуру.
Учитывая основные особенности иерархической модели ЭС, в практике возможны следующие подходы для оценки их состояний на основе универсальных моделей. Первый подход сводится к тому, что на основе множества значений параметров, оценивается состояние всей электронной системы
,
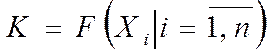(1.8)
где Xi – значение i-гo параметра; n – количество параметров.
Данный подход характеризуется тем, что он обладает простотой математических моделей, небольшим объемом вычислительных работ. Однако он не позволяет учесть основные особенности, характерные для ЭС.
Второй разработанный подход сводится к тому, что на основе значений параметров всей электронной системы строятся ее частные математические модели, каждая из которых описывает соответствующий уровень ее состояния.
Затем делается свертка этих моделей в универсальную математическую модель, на основе которой оценивается состояние всей электронной системы:
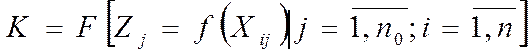, (1.9)
где Zj – j-я частная математическая модель; n0 – число частных математических моделей.
Данный подход характеризуется тем, что он имеет достаточно глубокое математическое обоснование используемых моделей, несколько больший объем вычислительных работ по сравнению с предыдущим подходом. При этом он позволяет учесть все основные особенности, характерные для ЭС.
Для обоих рассмотренных подходов характерно то, что они требуют наличия коэффициентов влияния параметров или соответствующих структур универсальной математической модели, которые являются отображениями весов ребер корневого графа декомпозируемой электронных системы.
1.4.2. Формализация технических процессов электронных систем
Известно, что любые исследования ЭC в процессе их разработки направлены на повышение их качества и надежности.
Выше отмечалось, что значение параметров электронной системы проявляются за счет наличия соответствующих отношений взаимодействия между их элементами. На уровне абстрактного понимания отношения взаимодействия показаны на рисунке 1.11.
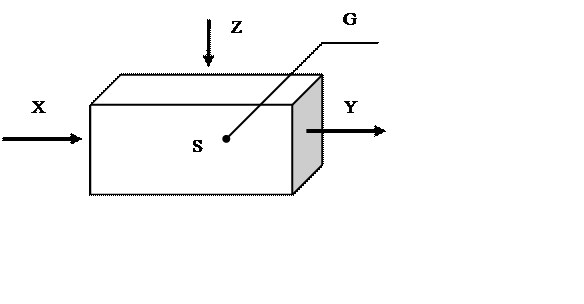
Рис. 1.11. Отношения взаимодействия между параметрами электронной системы:
S – исследуемая ЭС, G – параметры радиоэлементов, X – множество параметров входного воздействия, Y – множество параметров выходной функции, Z – множество факторов внешнего воздействия отражающих различную физическую природу, в частности, климатические – температура, влага, давление; механические – вибрация, звуковые удары; радиация – ядерная, солнечная, космическая; твердые частицы – песок, пыль, метеориты; грибки – плесень, различные грибковые соединения
Под входным воздействием считается переменная электрофизическая или физическая величина, вызывающая появление или изменение рассматриваемого процесса в схеме или конструкции. В качестве промежуточной характеристики понимается числовая величина, характеризующая определенное электрофизическое свойство элемента или взаимосвязь элементов схемы или конструкции ЭС.
Под выходной характеристикой понимается количественная величина или функция аргумента, описывающая характерные свойства проектирования электронных систем.
Под влиянием входного воздействия порождаются соответствующие процессы внутри ЭС. За счет возникающих отношений взаимодействия между ее элементами формируется выходная функция. При возникновении внешнего воздействия внутри объекта проявляются динамические изменения рассматриваемого процесса, это приводит к отклонению выходной функции, а значит к изменению значений ее параметров [13].
Очевидно, что по причинам указанным выше взаимодействие между параметрами электронной системы являются случайными, что отражается количественной мерой статистических связей между ними.
Между входными, промежуточными и выходными параметрами имеется в основном два вида связей - функциональные и корреляционные. При наличии функциональных связей между выходом и определяющими его параметрами X, G и факторами Z (рис. 1.11) можно найти такие соотношения, при которых удовлетворяются заданные значения выхода. Такая ситуация встречается крайне редко и только при анализе очень простых элементов конструкции. При этом наличие корреляционных связей между параметрами электронной системы требует знания их величин, которые в ряде случаев оказываются неизвестными или трудно определяемыми. Очевидно, основная трудность определения необходимых величин параметров электронной системы состоит в том, что оказываются неизвестными ни характер функциональных связей между ее параметрами, ни результаты длительных наблюдений за поведением ее элементов. Однако рассмотрение этого подхода представляет некоторый интерес, поскольку он позволяет во многих случаях получить первую количественную оценку связей между элементами ЭС.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.