ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
КРАСНОЯРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
Цифровая Обработка Сигналов
Лабораторная работа №4
Синтез и исследование цифровых фильтров с помощью программы SCANA. Исследование методов спектрального анализа сигналов на основе ДПФ.
Выполнил:
ст-т гр. Р53-4
Дергунов С.А.
Проверил:
Глинченко А. С.
Красноярск 2006
· Освоить методику анализа и изучить параметры и характеристики анализаторов амплитудного и фазового спектров сигналов на основе ДПФ.
· Изучить, как осуществляется анализ энергетических спектров (спектральной плотности мощности) дискретных случайных сигналов с помощью ДПФ методами периодограмм и коррелограмм.
Исходные данные:
1. Тип фильтра – ППФ.
2. Центральные частоты ППФ: f0i = 150 Гц.
3. Частоты среза-задерживания ППФ:
i. fС1 = 125 Гц; fС2 = 175, Гц;
ii. fЗ1 = 100 Гц; fЗ2 = 200 Гц.
4. Частоты среза-задерживания ФНЧ:
i. fС = 25 Гц, fЗ = 50 Гц.
5. Спад (ослабление) АЧХ на границах полосы пропускания: aп= 6 дБ.
6. Затухание АЧХ в полосе задерживания: aз ³ 46 дБ.
7. Форма АЧХ в полосе пропускания – монотонная.
8. Частота дискретизации: fд = 1000 Гц.
Найдем максимально возможный шаг анализа по частоте Dfmax и соответствующее ему минимальное значение ширины окна анализа N1min = fд/Dfmax исследуемого анализатора спектра на основе ДПФ.
Для частот f0, fc1, fc2, fз1, fз2 при условии совпадения их с бинами ДПФ Dfmax = 25 Гц, N1min = fд/Dfmax = 1000/25 = 40. Исходя из условия разрешения соседних частотных составляющих, им соответствуют Df = Dfmax/2 = 25/2 = 12,5 Гц, N1 = 2N1min = 80.
Найдем Nр ≥ 32×N1 + Nн = 2658. Возьмем Nр = 3000.
Сгенерируем полигармонический сигнал и шум:
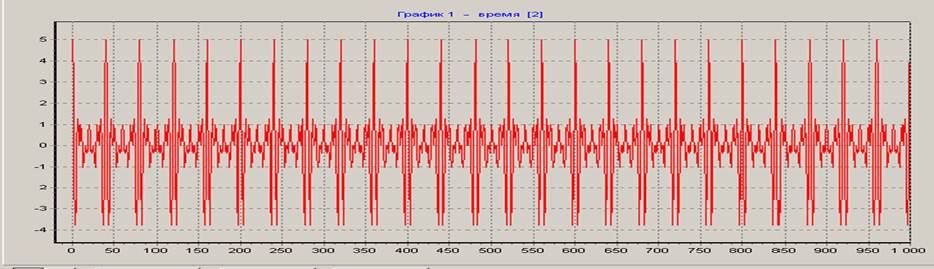
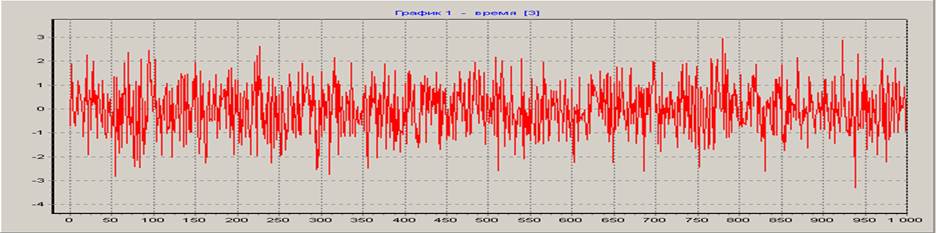
Синтезируем нерекурсивный цифровой фильтр. Характеристики фильтра:
ППФ, весовая функция – Хэмминга, N = 81, fС1 = 125 Гц; fС2 = 175 Гц.
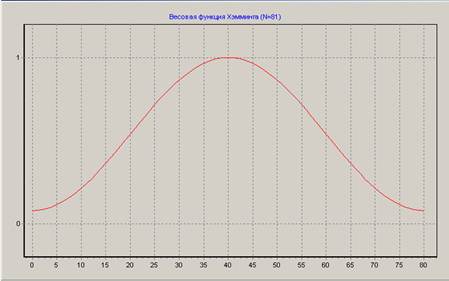
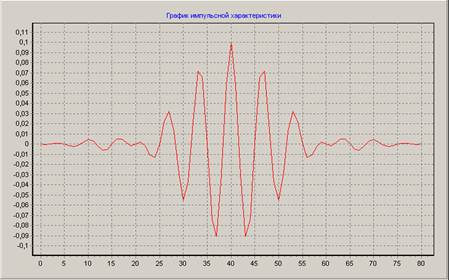
Амплитудно-частотная характеристика фильтра:
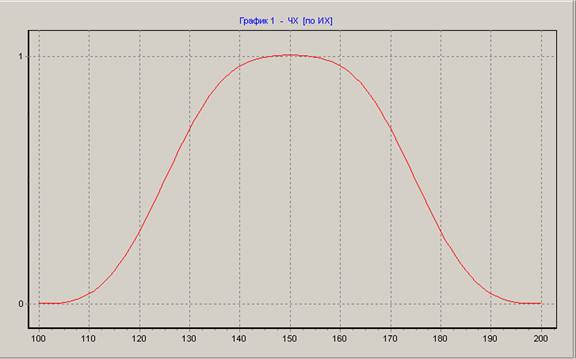
1. Гармонический анализ чистого полигармонического сигнала, действующего на входе НЦФ:
1. Прямоугольная функция:
при N = N1 = 80 при 1,25N1 = 1,25N = 100 при 2N1 = 2N= 160
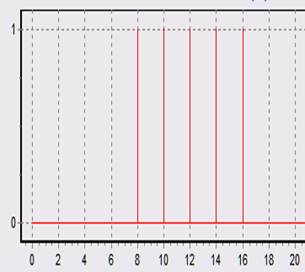
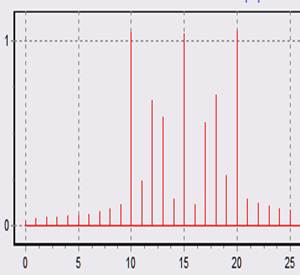
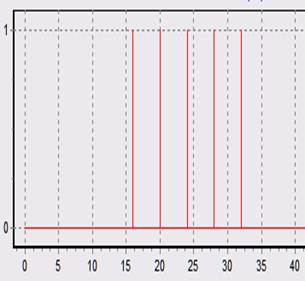
Проанализируем полученные графики. При N = N1 у нас шаг получается достаточным для разрешения всех составляющих сигнала. При увеличении N = 2N1 у нас все еще не наблюдается перекрытие главных лепестков частотных характеристик каналов, поэтому не ухудшается разрешающая способность анализатора спектра и картинка получается такая же, как и при N = N1. При N = 1.25N1 на сигналы откликаются 3 соседних каналов на уровне главных лепестков и все каналы ДПФ на уровне боковых лепестков, т.е. на картинке виден эффект размывания спектра.
2. Функция Хэмминга:
при N = N1 = 80 при 1,25N1 = 1,25N = 100 при 2N1 = 2N= 160
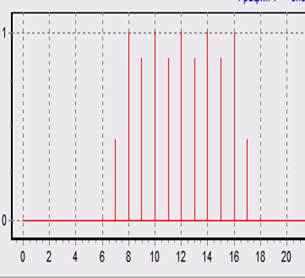
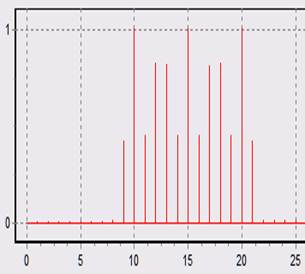
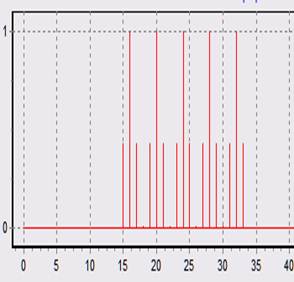
Здесь видно, что при увеличении N = 2N1 перекрываются главные лепестки частотной характеристики каналов, поэтому однозначное разрешение здесь не получается. Это связано с более широким главным лепестком, нежели у прямоугольной весовой функции. Также, как и с прямоугольной весовой функцией, при N=1.25N1 на сигналы откликаются 3 соседних каналов на уровне главных лепестков и все каналы ДПФ на уровне боковых лепестков, поэтому на картинке виден эффект размывания спектра.
2. Выполнить гармонический анализ входного полигармоничес-кого сигнала с наложенным на него шумом.
Весовая функция – прямоугольная; ширина окна анализа N1 = N = 80, число усредняемых окон L = 1, L = 32, начало окна Nн = 0.
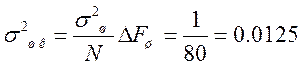 -
мощность шума.
-
мощность шума.
При L = 1 При L = 32
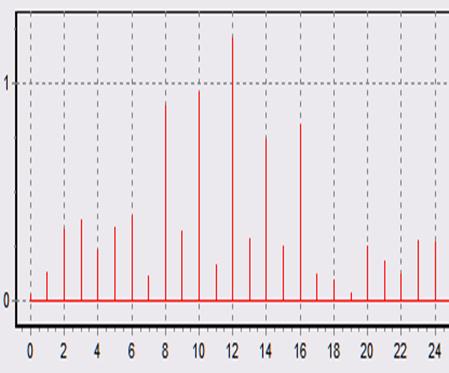
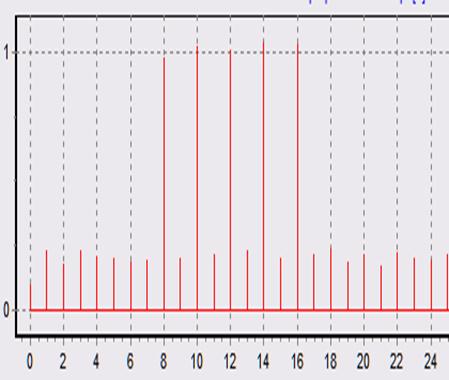
Усредняя 32 реализации сигнала мы повышаем точность оценки параметров сигнала, таких как амплитуда и фаза, при разброс шума уменьшается, стремясь к своему центральному значению. Этот процесс четко виден на графиках выше.
3. Выполнить анализ энергетического спектра случайного сигнала типа белый шум на выходе НЦФ методом периодограмм (Уэлча).
Весовые функции – прямоугольная, Хэмминга; ширина окна анализа (число точек ДПФ) N1 = N; число усредняемых окон L = 1, L = 32, начало окна Nн равно длине импульсной характеристики фильтра.
1. Прямоугольная функция:
При L = 32 При L = 1
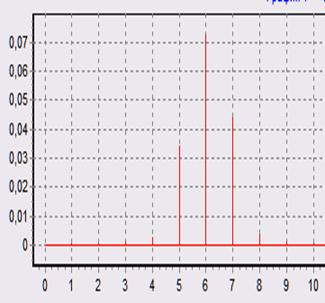
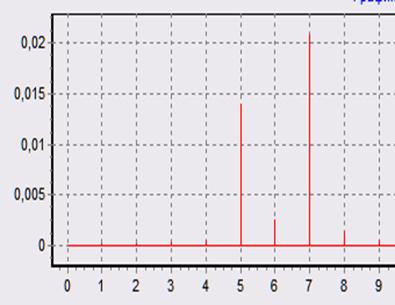
2. Функция Хэмминга:
При L = 32 При L = 1
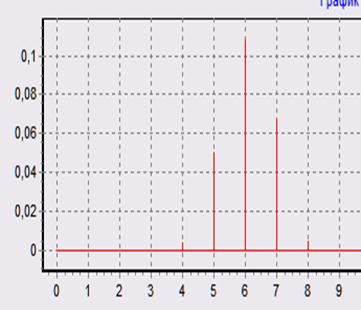
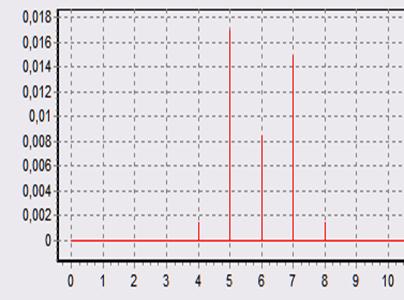
Наилучшей с точки зрения мощности шума является прямоугольная весовая функция, имеющая минимальную эквивалентную шумовую полосу. Это видно на графиках. Если рассчитать σ2шк, то для Хэмминга:
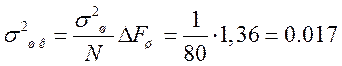 .
.
А для прямоугольной:
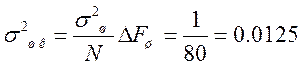 .
.
При усреднении видно возрастание мощности шума. Выражение для СПМ при вычислении методом периодограмм:
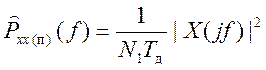
Значения L периодограмм:
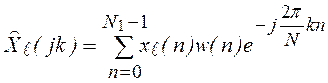
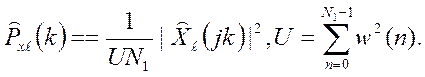
Усредненная периодограмма (оценка):
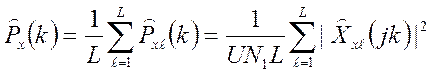
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.