Выполнил: ст. гр. Р 50-3Б
Непомнящих Г.А.
Проверил: Глинченко А. С.
Красноярск 2004 г.
Цель синтеза: Определение коэффициентов звеньев фильтра (b0, b1, b2, a1, a2).
Исходные данные на синтез ППФ для варианта v =3:
· тип фильтра – полосно-пропускающий (ППФ);
· центральная частота полосы пропускания f0i = 1560 Гц;
· нижняя частота среза fС1 = 1400 Гц;
· верхняя частота среза fС2 = 1720 Гц;
· нижняя частота задерживания fЗ1 = 1240 Гц;
· верхняя частота задерживания fЗ2 = 1880 Гц;
· допустимая неравномерность АЧХ в полосе пропускания ап = 0,5 дБ;
· затухание АЧХ в полосе задерживания аз ≥ 45 дБ;
· частота дискретизации fд = 7680 Гц.
·
Исходные данные на синтез ФНЧ для варианта v = 3:
· тип фильтра – нижних частот (ФНЧ);
· частота среза fС = 160 Гц;
· частота задерживания fЗ = 320 Гц;
· допустимая неравномерность АЧХ в полосе пропускания ап = 0,5 дБ;
· затухание АЧХ в полосе задерживания аз ≥ 45 дБ;
· частота дискретизации fд = 7680 Гц.
Отчёт к лабораторной работе:
-------------- Требования к АЧХ ЦФ ------------------
Неравномерность в полосе промускания Ап = 0,500
Затухание в полосе задерживания Аз = 45,000
Частота дискретизации Fd = 7680
Нормированная частота среза АФПНЧ = 1,0000000
Нормированная частота задерживания АФПНЧ = 1,9700000
------------------ Синтез АФПНЧ ---------------------
Аппроксимация Баттерворта (по Тейлору)
Порядок АФПНЧ = 10.
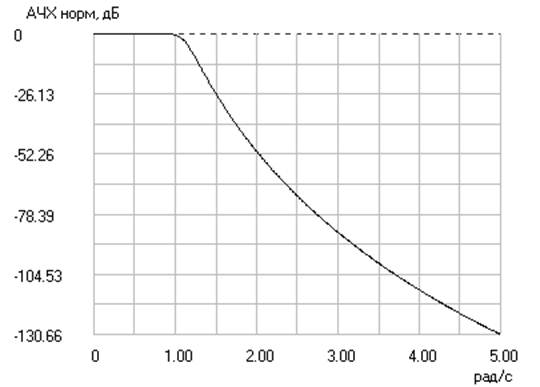
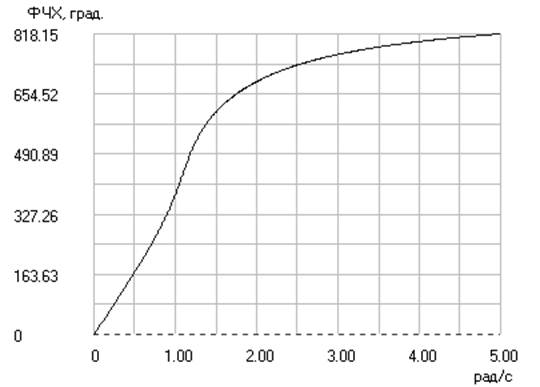
Аппроксимация Чебышева прямая
Порядок АФПНЧ = 6.
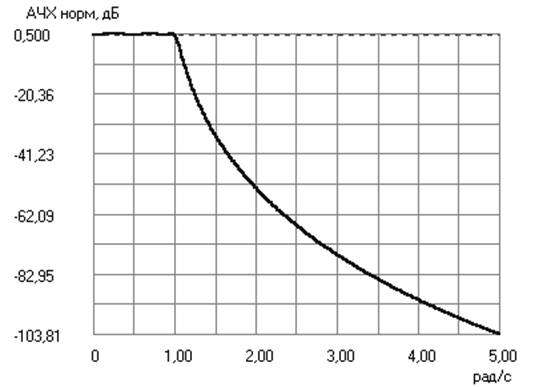
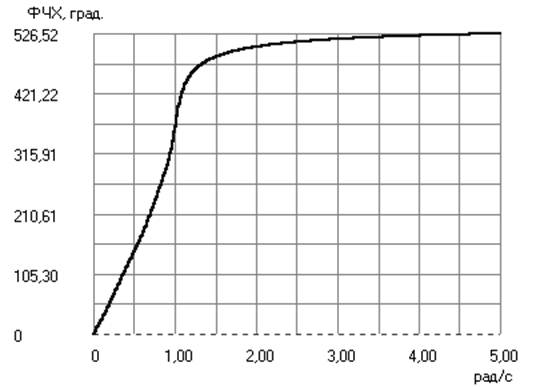
Аппроксимация Чебышева инверсная
Порядок АФПНЧ = 6.
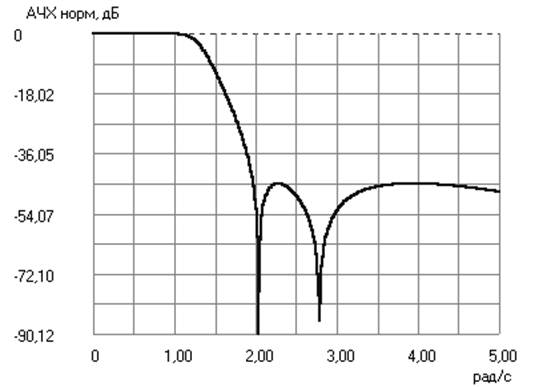
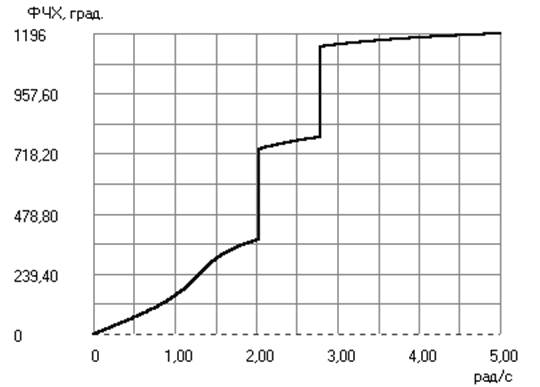
Выбираем вид рабочей аппроксимирующей функции из условия минимума порядка фильтра: Золотарева-Кауэра.
Аппроксимация Золоторева-Кауэра (эллиптическая)
Порядок АФПНЧ = 4.
---- Полюса АФПНЧ
Pp[1]=-0,442924775 + (0,464925865)*j
Pp[2]=-0,442924775 + (-0,464925865)*j
Pp[3]=-0,149740746 + (1,019852516)*j
Pp[4]=-0,149740746 + (-1,019852516)*j
---- Нули АФПНЧ
Pz[1]=0,000000000 + (4,838160429)*j
Pz[2]=0,000000000 + (-4,838160429)*j
Pz[3]=0,000000000 + (2,110324268)*j
Pz[4]=0,000000000 + (-2,110324268)*j
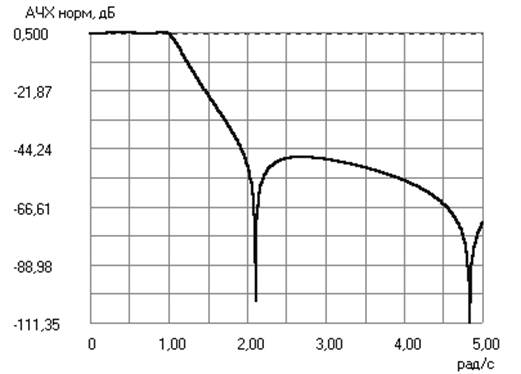
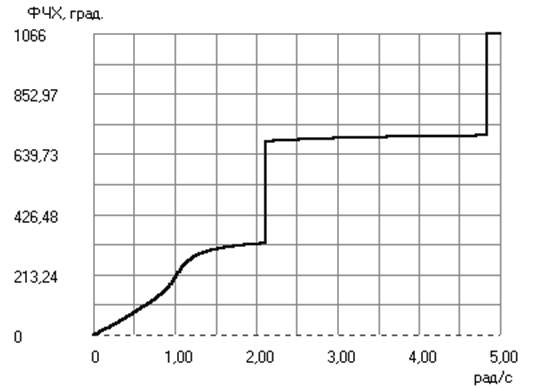
------ Результаты билинейного преобразования --------
Порядок ЦФ = 8
Нормирующий множитель фильтра С = 0,005353303881
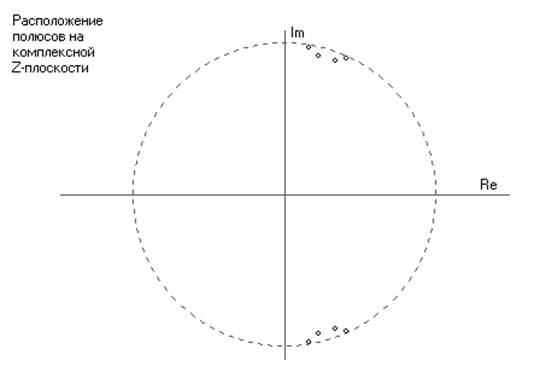
---- Полюса ЦФ
Zp[1]=0,331339915 + (-0,884506840)*j
Zp[2]=0,331339915 + (0,884506840)*j
Zp[3]=0,220129538 + (0,916401684)*j
Zp[4]=0,220129538 + (-0,916401684)*j
Zp[5]=0,157065193 + (0,967378222)*j
Zp[6]=0,157065193 + (-0,967378222)*j
Zp[7]=0,407406785 + (-0,893053962)*j
Zp[8]=0,407406785 + (0,893053962)*j
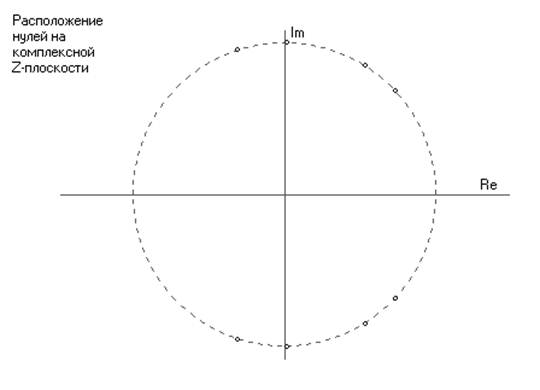
---- Нули ЦФ
Zz[1]=-0,312306687 + (0,949981333)*j
Zz[2]=-0,312306687 + (-0,949981333)*j
Zz[3]=0,728877593 + (0,684644035)*j
Zz[4]=0,728877593 + (-0,684644035)*j
Zz[5]=0,014991293 + (0,999887624)*j
Zz[6]=0,014991293 + (-0,999887624)*j
Zz[7]=0,528626355 + (0,848854626)*j
Zz[8]=0,528626355 + (-0,848854626)*j
Коэффициенты РЦФ каскадной формы реализации
Количество звеньев = 4
-------------------------------------------
b0[1]= 1 b1[1]= 0,624613373 b2[1]= 1 a1[1]= -0,66267983 a2[1]= 0,892138489
b0[2]= 1 b1[2]= -1,45775519 b2[2]= 1 a1[2]= -0,440259076 a2[2]= 0,888249061
b0[3]= 1 b1[3]= -0,029982586 b2[3]= 1 a1[3]= -0,314130386 a2[3]= 0,960490099
b0[4]= 1 b1[4]= -1,05725271 b2[4]= 1 a1[4]= -0,81481357 a2[4]= 0,963525668
Коэффициенты РЦФ параллельной формы реализации
Количество звеньев = 4
----------------------------------------------
b0[1]= -19,6674107 b1[1]= -3,30631186 b2[1]= 0 a1[1]= -0,66267983 a2[1]= 0,892138489
b0[2]= 23,3774838 b1[2]= -4,19065498 b2[2]= 0 a1[2]= -0,440259076 a2[2]= 0,888249061
b0[3]= -7,54807276 b1[3]= 4,43038847 b2[3]= 0 a1[3]= -0,314130386 a2[3]= 0,960490099
b0[4]= 4,14950547 b1[4]= 4,02259428 b2[4]= 0 a1[4]= -0,81481357 a2[4]= 0,963525668
Рассчитываем ЧХ РЦФ
Форма реализации фильтра: каскадная
Форма реализации звеньев: прямая
Число разрядов дробной части коэффициентов: 15 бит
Способ округления: округление
Графики частотных характеристик фильтра
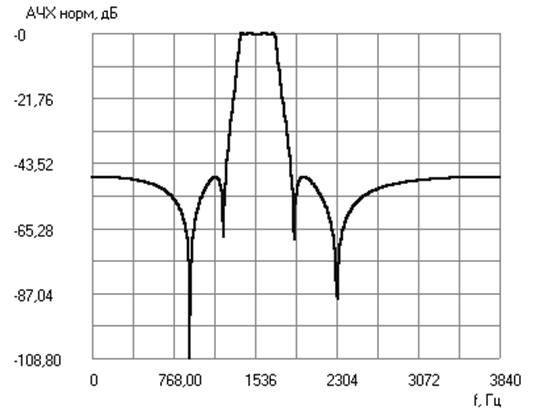
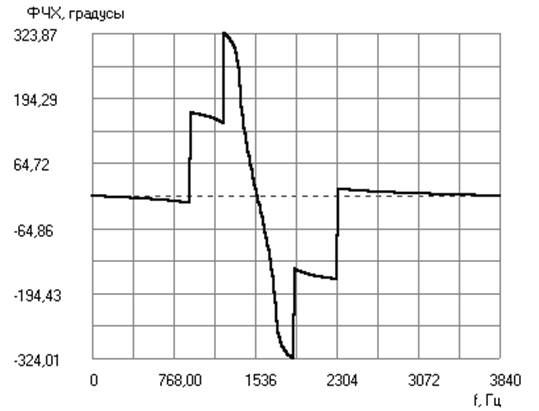
Значения АЧХ на частотах среза и задерживания:
А(fс1) = - 0,501 дБ; А(fс2) = - 0,497 дБ
А(fз1) = - 79,043 дБ; А(fз2) = - 48,542 дБ
График импульсной характеристики фильтра
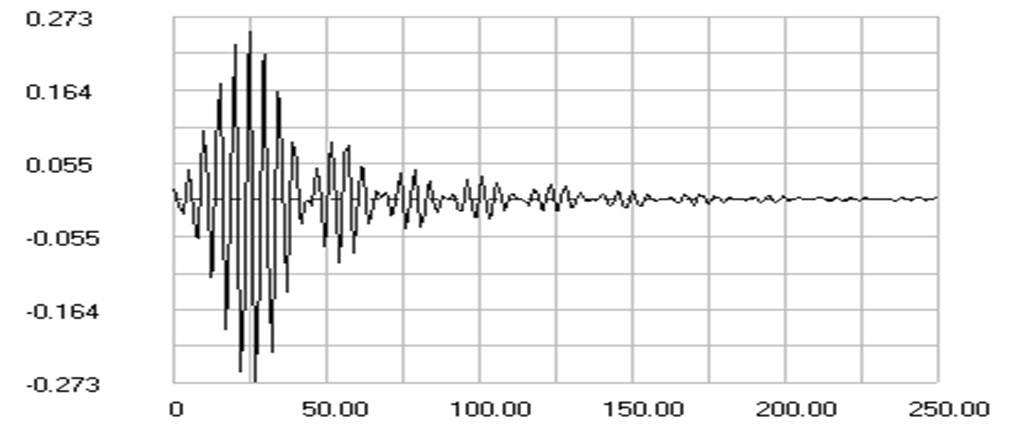
Значения масштабных множителей
---- Масштабные множители фильтра
Временной ММ = 0.15206353
Спектральный ММ = 0.33170963
Статистический ММ = 0.37535835
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.