Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального
Образования
КРАСНОЯРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
Кафедра “Радиосистемы”
КУРСОВОЙ ПРОЕКТ
Проектирование автоматической системы слежения за направлением
Пояснительная записка
Выполнил:
Студент гр. Р53-4
Д.С. Титов
Проверил:
В.Н. Бондаренко
Красноярск 2006
Содержание
1 Задание на курсовой проект……………………………………………………3
2 Исходные данные……………………………………………………………….4
3 Задание 1……………………………………………………………...................5
4 Задание 2..……………………………………………………………………….7
5 Задание 3……………………………………………………………………….12
6 Задание 4……………………………………………………………………….14
7 Задание 5…………………………………………………………………….…18
Выводы………………………………………………………………………...…20
1 Задание на курсовой проект
Для заданной структурной схемы следящей системы и моделей задающего воздействия x(t) и помехи n(t) выполнить следующее:
1) Определить передаточные функции разомкнутой системы Кр(р), а также замкнутой системы Кз(p); спектральную плотность Nэ эквивалентных флуктуаций, приведенных ко входу дискриминатора.
2) Произвести оптимизацию следящей системы по параметру Ku, используя критерий минимума среднего квадрата ошибки; определить оптимальное значение шумовой полосы Fш системы и минимально достижимую ошибку слежения еmin; построить графики зависимости результирующей средней квадратической ошибки слежения, а также её составляющих (динамической и шумовой) от полосы.
3) Построить логарифмические амлитудно-частотную (ЛАХ) и фазочастотную (ЛФХ) характеристики разомкнутой системы и определить по ним запас устойчивости по амплитуде и фазе при оптимальном значении параметра Ku.
4) Произвести моделирование следящей системы на ЭВМ при двух типах воздействия: а) ступенчатом; б) квадратичном; построить графики переходного процесса и определить качественные показатели системы в переходном режиме (быстродействие, перерегулирование).
5) Составить функциональную схему следящей системы заданного типа (схема должна также содержать функциональные элементы устройства поиска и обнаружения сигнала).
2 Исходные данные
Вариант №20
Тип следящей системы: Автоматической система слежения за направлением;
Параметры задающего воздействия:
Начальное ускорение: X2=0,25 град/с2 ;
Коэффициент передачи дискриминатора: kd=1,2 В/град;
Спектральная плотность шума: N0=0,5 Вт/Гц;
Параметры динамического звена:
T1=0.15c
Число интеграторов k=2,
Порядок дифференциального уравнения описывающего систему n=2,
Число форсирующих звеньев m=1,
Область применения: фазовый пеленгатор РТС траекторных измерений.
3 Задание 1
1) Определить передаточные функции разомкнутой системы Кр(р);
2) Определить передаточные функции замкнутой системы Кз(p);
3) Определить спектральную плотность NЭ эквивалентных флуктуаций, приведенных ко входу дискриминатора.
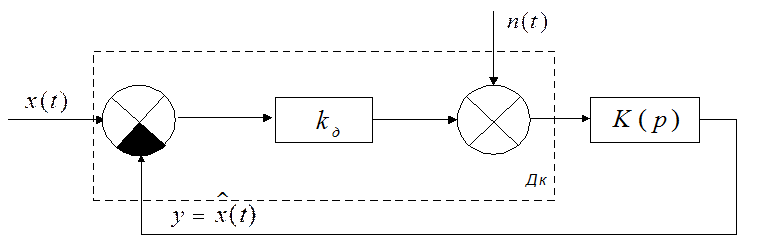
Рисунок 1. Схема линейной следящей системы
По исходным данным, два интегрирующих звена k=2, одно форсирующее звено m=1 и два инерционных n=2, определяем передаточную функцию динамического звена:
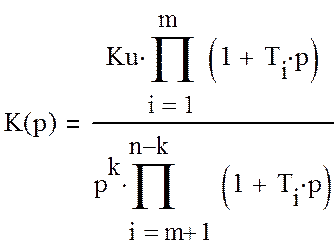 (1)
(1)
в данном случае передаточная функция динамического звена будет:
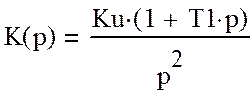 (2)
(2)
Для разомкнутой системы передаточная функция находится перемножением коэффициента передачи дискриминатора и передаточной функции динамического звена:
![]() (3)
(3)
Передаточная функция разомкнутой системы:
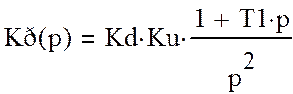 (4)
(4)
Передаточная функция замкнутой системы:
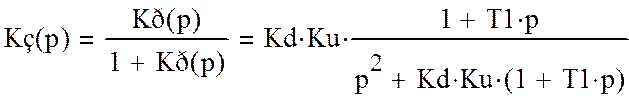 (5)
(5)
Для определения спектральной плотности Nэ эквивалентного шума, приведенного ко входу дискриминатора воспользуемся правилом преобразования структурных схем (перенос сумматора с выхода на вход звена). Получим преобразованную структурную схему:
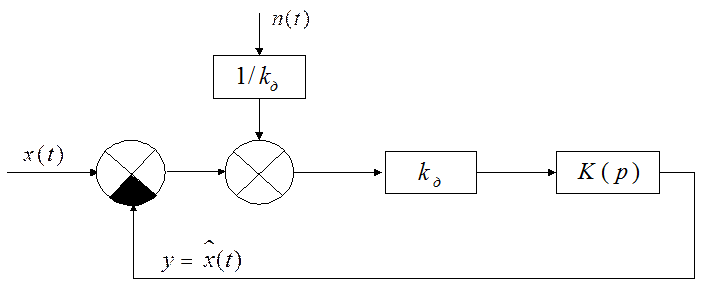
Рисунок 2. Преобразованная структурная схема следящей системы
Спектральная плотность эквивалентного шума будет равна:
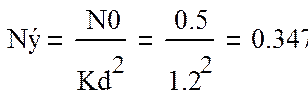
Вт/Гц (6)
4 Задание 2
1) Произвести оптимизацию передаточной функции разомкнутой системы, по параметру Ku, используя критерий минимума среднего квадрата ошибки;
2) Определить оптимальное значение шумовой полосы Fш системы и минимально допустимую ошибку слежения emin;
3) Построить графики зависимостей результирующей средней квадратической ошибки слежения, а также её составляющих (динамической и шумовой) от полосы.
Оптимизация системы по критерию минимума среднего квадрата ошибки сводится к нахождению параметра Ku, при котором обеспечивается минимум величины ē2=е2д+σ2е. Составляющая ед определяет динамическую ошибку, обусловленную инерционностью следящей системы по отношению к меняющемуся задающему воздействию, а составляющая σ2е определяет дисперсию шумовой ошибки, обусловленной помехой n(t).
В данном случае, для рассматриваемой системы 2-го порядка, порядок астатизма равен 2, следовательно динамическая ошибка определяется как:
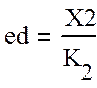 (7)
(7)
где К2 – добротность системы по ускорению.
Случайная составляющая ошибки определяется статистическими характеристиками помехи n(t) и структурой (а также параметрами) системы. В качестве n(t)используют модель белого шума с равномерной в полосе частот от 0 до ∞ спектральной плотностью. Дисперсию шумовой ошибки рассчитывают по формуле:
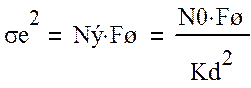 (8)
(8)
где Fш - шумовая полоса следящей системы в Гц.
Определим шумовую полосу рассматриваемой системы:
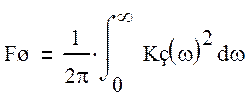 (9)
(9)
Передаточная функция замкнутой системы:
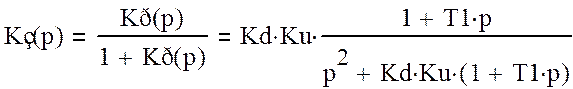 (10)
(10)
Заменим в формуле (10) параметр p на jw , получим выражение для комплексного коэффициента передачи замкнутой системы:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.