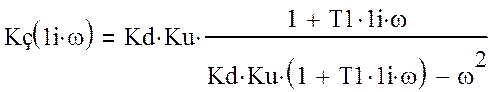 (11)
(11)
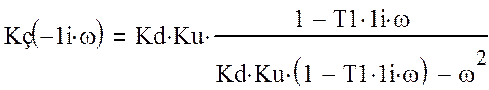 (12)
(12)
Тогда квадрат модуля комплексного коэффициента передачи (квадрат АЧХ):
![]() (13)
(13)
Преобразуя получаем:
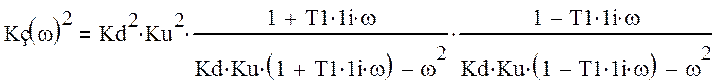 (14)
(14)
Представим Кз2(ω) в виде:
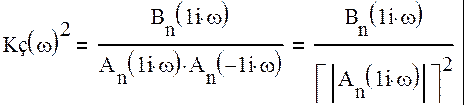 (15)
(15)
где полиномы An(jω) и Bn(jω):
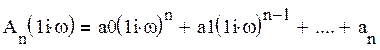 (16)
(16)
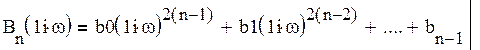 (17)
(17)
где n – порядок дифференциального уравнения, описывающего систему, для исследуемой системы n=2.
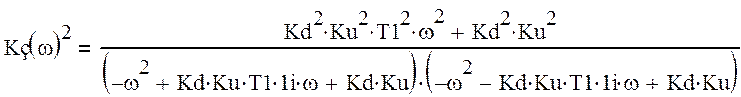 (18)
(18)
Коэффициенты полиномов:
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
Нахождение шумовой полосы системы и дисперсии шумовой ошибки сводится к вычислению интеграла:
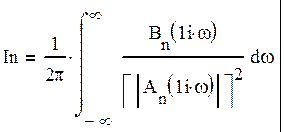 (24)
(24)
т.к n=2 то:
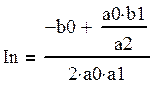 (25)
(25)
Подставляя коэффициенты полиномов получаем:
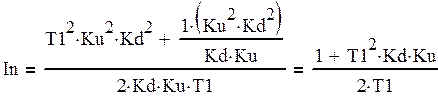 (26)
(26)
Шумовая полоса системы:
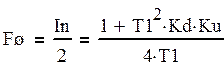 (27)
(27)
Дисперсия шумойвой ошибки:
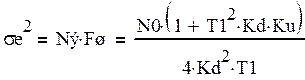 (28)
(28)
Произведем оптимизацию системы по параметру Ku:
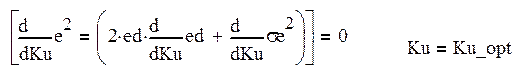 (29)
(29)
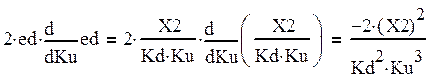 (30)
(30)
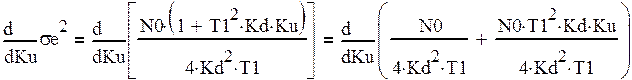 (31)
(31)
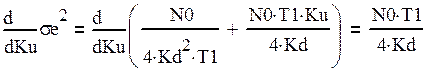 (32)
(32)
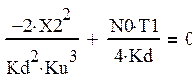 (33)
(33)
Из последнего уравнения находим:
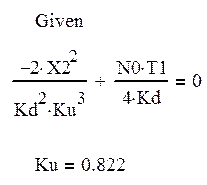 (34)
(34)
Оптимальное параметра Ku :
Ku=0,822
Оптимальное значение шумовой полосы:
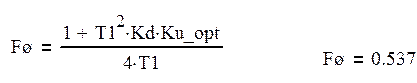 (35)
(35)
Дисперсия шумовой ошибки и динамическая ошибка при Ku = Ku_opt:
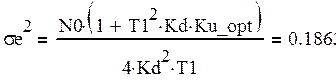 (36)
(36)
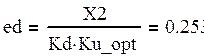 (37)
(37)
Минимально достижимая ошибка слежения:
![]() (38)
(38)
Физический смысл существования оптимального значения полосы Fш объясняется следующим. При малых значениях Fш основной вклад в результирующую ошибку ![]() вносит составляющая eд, а при больших Fш
- шумовая составляющая σe. Поэтому
существует оптимальное значение шумовой полосы Fшopt, при котором результирующая ошибка минимальна. Это
можно увидеть из графиков зависимости ошибок слежения шумовой полосы системы:
вносит составляющая eд, а при больших Fш
- шумовая составляющая σe. Поэтому
существует оптимальное значение шумовой полосы Fшopt, при котором результирующая ошибка минимальна. Это
можно увидеть из графиков зависимости ошибок слежения шумовой полосы системы:
![]() (39)
(39)
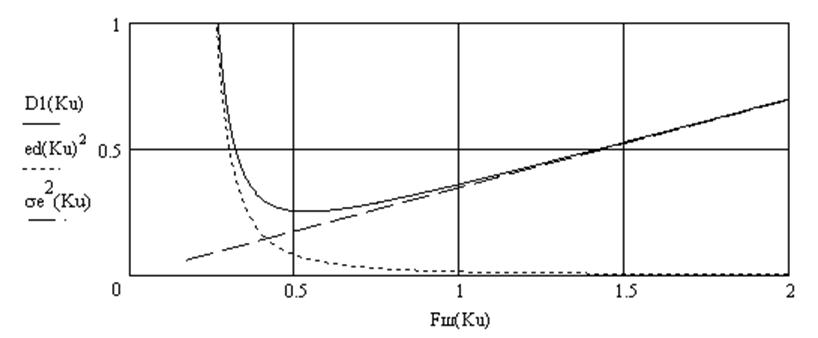
Рисунок 3. График зависимости ошибок слежения от шумовой полосы
системы
По графику видно, что минимальное значение результирующей ошибки будет при Fш =0,54 . Это значение точно соответствует Fш_opt..
5 Задание 3
1) Построить ЛАХ и ЛФХ разомкнутой системы и определить по ним запас устойчивости по амплитуде и по фазе при оптимальном значении Ku_opt.
Определим запас устойчивости системы, используя метод логарифмических частотных характеристик, суть которого сводится к построению ЛАХ и ЛФХ разомкнутой следящей системы.
Коэффициент передачи разомкнутой системы:
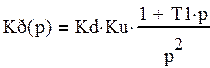 (40)
(40)
Представим систему в виде трех последовательно соединеных типовых звеньев. АЧХ такой системы бедет:
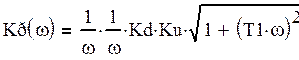 (41)
(41)
ЛАХ этой системы:
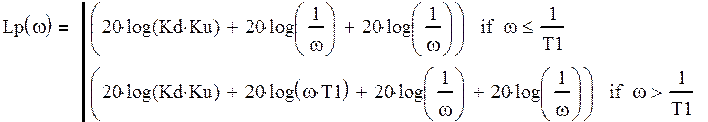 (42)
(42)
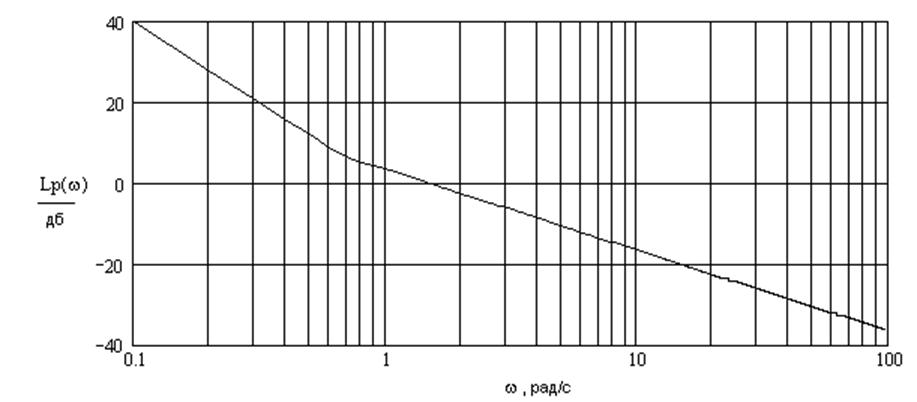
Рисунок 4. ЛАХ разомкнутой системы
ЛФХ этой системы:
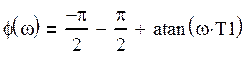 (43)
(43)
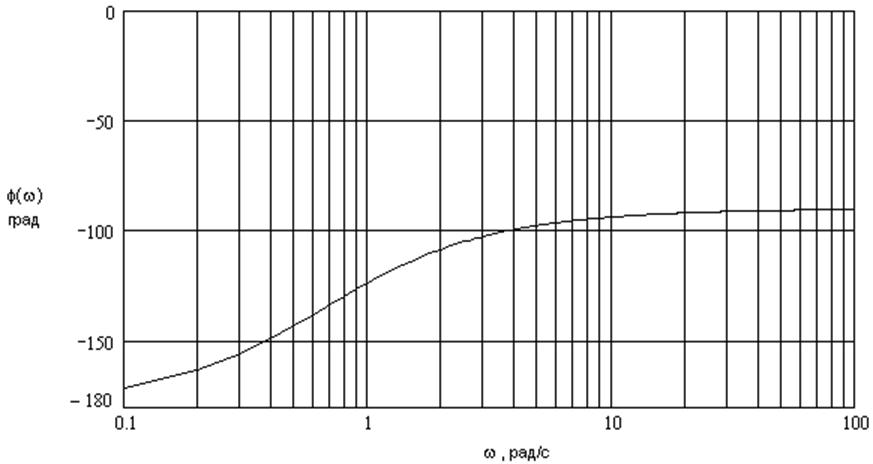
Рисунок 5. ЛФХ разомкнутой системы
Определим частоту среза ωср. Для этого приравняем к нулю формулу (42) и воспользуемся стандартными функциями для решения полученного уравнения:
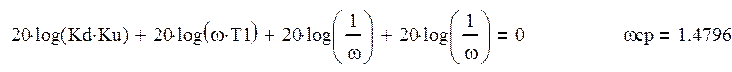 (44)
(44)
Определим запас устойчивости по фазе Δφ – это угол, равный:
![]() (45)
(45)
Это удовлетворяет условию достаточного запаса устойчивости системы по фазе: Δφ > 30°.
Запас устойчивости по амплитуде не определяем т.к. отсутствует критическая частота.
6 Задание 4
1) Произвести моделирование следящей системы на ЭВМ при двух типах воздействия: а) ступенчатом; б) квадратичном; построить графики переходного процесса и определить качественные показатели системы в переходном режиме (быстродействие, перерегулирование).
При моделировании линейной непрерывной системы по ее передаточной функции, будем использовать метод билинейного преобразования. Суть его состоит в том, что непрерывные интегрирующие звенья, входящие в систему, заменяют дискретными интеграторами, осуществляющими интегрирование по методу трапеций.
Дискретная передаточная функция
цифровой модели следящей системы, при использовании метода билинейного
преобразования, получается из передаточной функции замкнутой непрерывной
системы Кз(р) путем замены оператора непрерывного интегрирования: 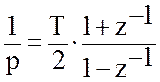 , где T -
интервал дискретизации, выбираемый в соответствии с теоремой Котельникова из
условия
, где T -
интервал дискретизации, выбираемый в соответствии с теоремой Котельникова из
условия 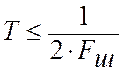 (реально выбирается приблизительно
на порядок меньше, чтобы исключить накопление ошибок из-за округления чисел).
(реально выбирается приблизительно
на порядок меньше, чтобы исключить накопление ошибок из-за округления чисел).
Полученную в результате дискретной аппроксимации передаточную функцию цифровой модели необходимо представить в виде:
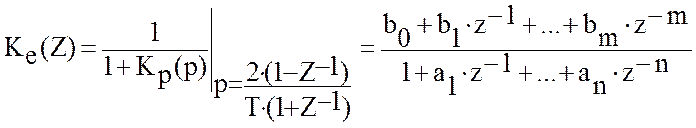 (46)
(46)
Этой передаточной функции соответствует разностное уравнение:
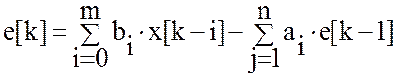 (47)
(47)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.