КРАСНОЯРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ПОГРЕШНОСТИ ИЗМЕРЕНИЙ ФИЗИЧЕСКИХ ВЕЛИЧИН И ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Выполнил: ст. гр. Р24-1
Степанов Д.А.
Проверил: Квашнин Г.М.
Краткая теория.
1. Провести измерения 30 раз.
2. Вычислить среднее арифметическое значение по формуле .
![]()
![]()
![]() 1)
1) 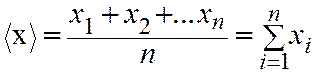 .
.
3. Задать доверительную вероятность a. Доверительной вероятностью называют вероятность нахождения истинного значения измерения в некотором интервале (доверительном). Доверительный интервал – это интервал, в котором находятся истинное значение измеряемой величины.
4. По таблице 1 найти коэффициент Стьюдента, соответствующий заданной доверительной вероятности a и числу измерений 30 отрезков.
|
Число |
Доверительная вероятность a |
||||||
|
измерений n |
0,6 |
0,7 |
0,95 |
0,98 |
|||
|
2 |
1,38 |
2,0 |
12,7 |
31,8 |
|||
|
3 |
1,06 |
1,3 |
4,3 |
7,0 |
|||
|
4 |
0,98 |
1,3 |
3,2 |
4,5 |
|||
|
5 |
0,94 |
1,2 |
2,8 |
3,7 |
|||
|
6 |
0,92 |
1,2 |
2,6 |
3,4 |
|||
|
7 |
0,90 |
1,1 |
2,4 |
3,1 |
|||
|
8 |
0,90 |
1,1 |
2,4 |
3,0 |
|||
|
9 |
0,90 |
1,1 |
2,3 |
2,9 |
|||
|
10 |
0,88 |
1,1 |
2,3 |
2,8 |
|||
|
30 |
0,84 |
1,0 |
2,0 |
2,3 |
|||
5.
Абсолютная погрешность характеризует случайную ошибку измерения. Вычислить
абсолютную погрешность по формуле 2)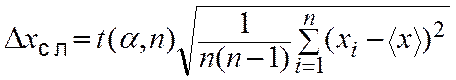 ,
и сравнить ее с аппаратурной. Для дальнейших вычислений взять ту, которая из
них больше.
,
и сравнить ее с аппаратурной. Для дальнейших вычислений взять ту, которая из
них больше.
6.
По формуле 3)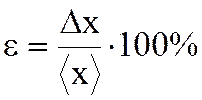 . вычислить относительную
ошибку e. Относительная ошибка – это физическая величина,
используемая для оценки точности измерения.
. вычислить относительную
ошибку e. Относительная ошибка – это физическая величина,
используемая для оценки точности измерения.
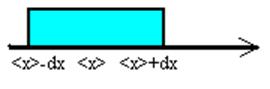
7. Записать окончательный результат в виде формулы и доверительного интервала.
4) x=<x>±Dx.
Практическая часть.
1. Начертим произвольно от руки (без применения линейки) 30 приблизительно равных по длине отрезков. Измерим каждый из них. Все полученные данные занесем в таблицу 2.
Таблица 2
|
n |
l(i) |
<I> |
deltl(i) |
(deltl(I))^2 |
Sn |
|
1 |
34 |
35,367 |
-1,4 |
1,867 |
0.649 |
|
2 |
36 |
0,6 |
0,401 |
||
|
3 |
35 |
-0,4 |
0,134 |
||
|
4 |
39 |
3,6 |
13,201 |
||
|
5 |
41 |
5,6 |
31,734 |
||
|
6 |
42 |
6,6 |
44,001 |
||
|
7 |
32 |
-3,4 |
11,334 |
||
|
8 |
38 |
2,6 |
6,934 |
||
|
9 |
31 |
-4,4 |
19,067 |
||
|
10 |
33 |
-2,4 |
5,6011 |
||
|
11 |
36 |
0,6 |
0,401 |
||
|
12 |
37 |
1,6 |
2,667 |
||
|
13 |
32 |
-3,4 |
11,334 |
||
|
14 |
30 |
-5,4 |
28,801 |
||
|
15 |
35 |
-0,4 |
0,134 |
||
|
16 |
38 |
2,6 |
6,934 |
||
|
17 |
40 |
4,6 |
21,46 |
||
|
18 |
36 |
0,6 |
0,401 |
||
|
19 |
42 |
6,6 |
44,001 |
||
|
20 |
34 |
-1,4 |
1,867 |
||
|
21 |
29 |
-6,4 |
40,534 |
||
|
22 |
32 |
-3,4 |
11,334 |
||
|
23 |
35 |
-0,4 |
0,134 |
||
|
24 |
33 |
-2,4 |
5,601 |
||
|
25 |
30 |
-5,4 |
28,801 |
||
|
26 |
37 |
1,6 |
2,667 |
||
|
27 |
38 |
2,6 |
6,934 |
||
|
28 |
32 |
-3,4 |
11,334 |
||
|
29 |
36 |
0,6 |
0,401 |
||
|
30 |
38 |
2,6 |
6,934 |
2. Посчитаем среднее значение по формуле 1. Среднее значение равно
35.367
3. Находим среднеквадратичную ошибку по след. Формуле
Sn=0.649
4. Получим абсолютную ошибку по след формуле 2). (учитывая что коэффициент Cтьюдента равен 1 при a=0.7)
DX=0.649
5.
В заключении найдем относительную
ошибку по формуле 3).
e=1.8%
Построим по данной таблице следующую гистограмму.
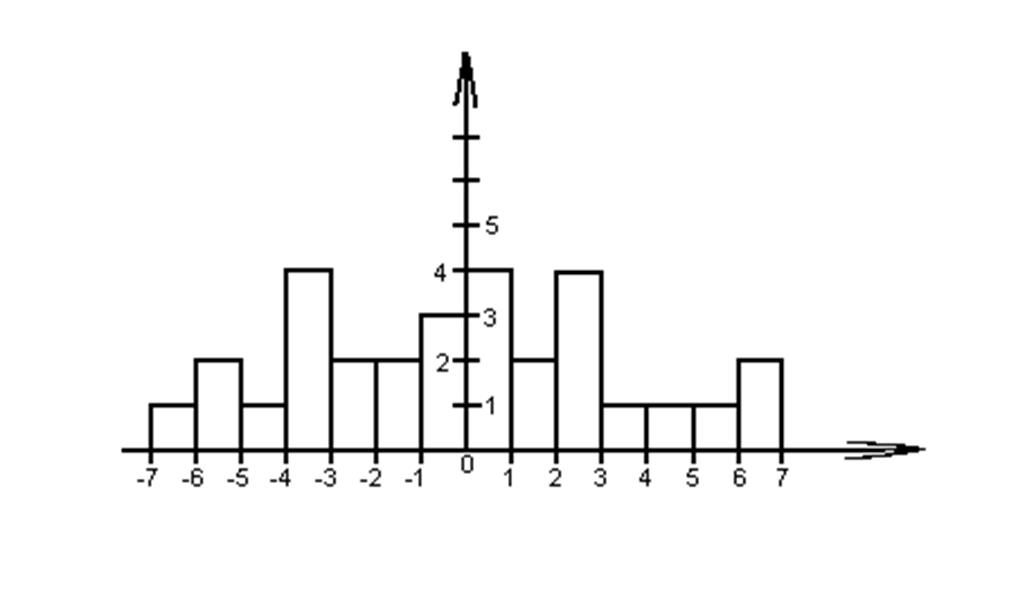
6. Вывод: Я изучил теорию погрешности, применяя ряд формул. Получил, что средняя квадратичная ошибка равна 0.649. Абсолютная ошибка при коэффициенте Стьюдента равному 1 и a равному 0.7 равна 0.649 . Я убедился, что вследствие неточности измерительный приборов и трудностей всех побочных явлений, при измерениях неизбежно возникают погрешности различных измерений. Вследствие чего вычислил относительную ошибку, в моей лабораторной работе она равна 1.8%.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.