Оптимальное планирование закупок при случайном спросе на товары, страница 10

Определение оптимальных размеров заказов товаров

Случайность спроса на товары, выраженная  в виде распределения (10), требует учета рисков при формировании запасов. Риски связаны с иммобилизацией финансовых ресурсов в избыточных запасах и с упущенной выгодой компании из-за недостатка товаров. Оптимальным считается заказ (запас), минимизирующий общие потери, определяемые через штрафные функции. Модели, формализующие задачи подобного типа, называют моделями хозяйственного риска. В данном случае, используя эту модель, следует определить оптимальные в указанном смысле объемы заказов всех товаров группы А.

Модель хозяйственного риска представляет собой минимизируемую функцию общих потерь компании

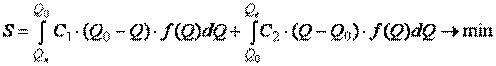
где:  Q0 – искомый оптимальный объем заказа, определяемый в интервале доверительных границ { Qв ≥ Q0 ≥ Qн };

f(Q) – распределение спроса (10);

C1, C2 – потери при заказе единицы товара.

C1 = Cх + 0.01γ ∙Cи,

С2 = Сп – Си;

γ  - банковская ставка, % (табл.3). Дополнительным ограничением является условие непревышения бюджета группы А

S0 = Q0∙Cи ≤ BA

Первый интеграл в целевой функции (11) в пределах  соответствует потерям от заказа лишних, невостребованных потребителями, товаров (избыточность запасов), а второй интеграл в пределах – упущенной выгоде из-за нехватки товаров.

Рис. 2. Графическое представление модели:

1, 2 - соответствующие потерям штрафные функции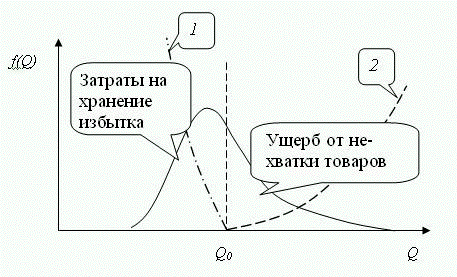

Поскольку средства Excel не позволяют вычислять интегралы напрямую, следует заменить их суммами с конечными пределами (Qн и Qв)

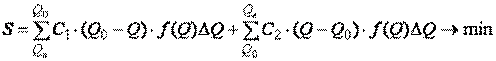
где DQ - интервал дискретизации диапазона изменения спроса.

Для расчётов интервал дискретизации следует принять равным ΔQ =1.

Расчёт составляющих общих издержек (табл.8) следует производить во всём диапазоне спроса (на всём интервале), но суммируются только издержки с положи тельным знаком (условное суммирование). К примеру, встроенная функция условного суммирования данных в столбце D имеет следующий вид

=СУММЕСЛИ(D16:D63;">0")