Лабораторная работа №11:
«Исследование преобразований спектров при дискретизации сигналов по времени
в системах ЦОС»
1. Цель лабораторной работы
Целью лабораторной работы является закрепление теоретических знаний о преобразованиях сигналов из аналоговой формы в цифровую путем экспериментального исследования их с помощью измерительных средств аппаратно-программного комплекса «АРМЭКС».
2. Задачи лабораторной работы
К задачам лабораторной работы относится:
установление связи между спектрами аналогового и дискретного сигналов путем их измерения;
определение искажений, обусловленных дискретизацией сигналов по времени;
обоснование условий выбора частоты дискретизации для сигналов различного вида;
анализ свойств дискретных шумовых сигналов;
оценка влияния входного аналогового фильтра нижних частот при дискретизации сигналов по времени;
ознакомление с аппаратными средствами дискретизации сигналов по времени и преобразования в цифровую форму, освоение методов экспериментального измерения параметров и спектров дискретных сигналов.
3. Теоретические сведения по работе
Лабораторная работа выполняется на основе теоретического материала, изложенного в главе 1 учебного пособия Глинченко А. С. Цифровая обработка сигналов. 2-е издание. Красноярск: ИПЦ КГТУ, 2005.
Ниже приводятся теоретические сведения, необходимые для расчета данных, используемых в процессе выполнения лабораторной работы в соответствии с заданием на подготовку к работе пункта 6.1, а также при обработке результатов измерения.
3.1. Расчет необходимой длины реализации сигнала при спектральных измерениях.
Измерение спектра дискретного (цифрового) сигнала осуществляется по его реализации конечной длины Тр = NТд, где Тд – период дискретизации сигнала по времени, N – число выборок сигнала на длине реализации, которое является параметром анализатора спектра. Значение этого параметра должно быть рассчитано и задано до проведения измерения. Оно находится из условия однозначного разрешения всех частотных составляющих, присутствующих в спектре периодического сигнала, и условия обеспечения необходимой точности измерения.
Значения
амплитуд Х(fk) спектральных
составляющих сигнала x(n)
вычисляются с помощью дискретного преобразования Фурье (ДПФ):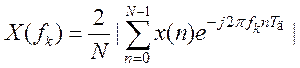 
. При k
= 0 
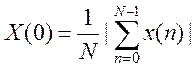. Вычисление выполняется на
дискретных частотах fk = kfд/N = kDfа в
полосе частот (0–fд/2), где k = 0, 1, 2, … (N–1)/2 – номер
частотной выборки спектра, Dfа = fд/N – шаг анализа спектра по частоте.
Шагу анализа Dfа должны быть кратны частоты основной и высших гармоник сигнала: F = рDfа, где р = 1, 2, … – число периодов сигнала на длине реализации N. При невыполнении этого условия происходит размывание или просачивание спектра сигнала между каналами анализатора спектра, что затрудняет или делает невозможным однозначное разрешение его спектральных составляющих.
Для однозначного разрешения спектральных составляющих сигнала в соответствии с условием F = рDfа на длине реализации сигнала должно укладываться целое число его периодов: рТ = NТд. Отвечающие этому условия значения длины реализации сигнала N находятся из соотношения:
fд/F = N /р.
Если значения fд и F представляют собой целые числа одинаковой размерности (Гц, кГц), то в качестве N и р можно принять N = fд, р = F. При этом N не должно превышать аппаратно допустимого максимального значения: N < Nmax, Nmax = 2046.
Чтобы уменьшить N, нужно найти общий делитель D чисел fд и F (на который они делятся без остатка). Тогда N = fд/D, р = F/D.
Наименьшие значения N и р получаются при делении fд и F на их наибольший общий делитель (НОД) Dн: N = fд/Dн, р = F/Dн.
Значению Dн = F (р = 1) соответствует минимально возможное значение длины реализации Nmin= fд/F.
Полученное таким образом значение N может быть увеличено в целое число раз (например, в 2 и более раза) для уменьшения шага анализа по частоте Dfа = fд/N, что увеличивает частотное разрешение анализатора спектра. При этом должно выполняться условие: N < Nmax = 2046. Также нужно иметь в виду, что от значения N зависит случайная погрешность спектральных измерений параметров сигнала, обусловленная внешними и внутренними шумами измерителя, в том числе шумами квантования АЦП. Она связана с эквивалентной шумовой полосой каналов анализатора спектра, определяемой как: DFш = α(fд/N), где α – коэффициент, зависящий от типа используемой весовой функции; для прямоугольной весовой функции α = 1, треугольной 1,33, Хэмминга 1,36.
Пример 1 определения числа выборок N. Пусть F = 300 Гц, fд = 8000 Гц. Для этих данных записываем отношение fд/F = 8000/300 = N /р. Возможное значение N = 8000 превышает Nmax. Поэтому находим общий делитель чисел 8000 и 300. Им является значение D = 100. Ему соответствуют значения N = 8000/D = 80, р = 300/D = 3. Общий делитель D одновременно является и наибольшим общим делителем Dm, поэтому найденное значение N является наименьшим из его возможных значений. Ему соответствует шаг анализа по частоте Dfа = fд/N = 8000/80 = 100 Гц.
Для повышения разрешения по частоте значение N можно увеличить в 2 раза и принять N = 160; при этом Dfа = 50 Гц.
Для обеспечения исходного разрешения по частоте Dfа = 100 Гц при увеличении частоты дискретизации в 2 раза (fд = 16000 Гц) нужно N также увеличить в 2 раза, т. е. выбрать N = 160.
Пример 2 определения числа выборок N. Пусть F = 3650 Гц, fд = 10000 Гц. Для этих данных fд/F = 10000/3650. Выберем D = 50. Тогда fд/F = (10000/50)/(3650/50) = 200/73 = N /р. Отсюда N = 200, р = 73, Dfа = 50 Гц. При N = 400 Dfа = 25 Гц. Выбрав N = 1000, получим Dfа = 10 Гц.
3.2. Расчет максимальной частоты спектра импульсных аналоговых сигналов
При обосновании выбора частоты дискретизации аналоговых сигналов с неограниченным по частоте спектром необходимо исходить из эффективной (условной) ширины спектра сигнала или его максимальной частоты Fm, определяемой в соответствии с тем или иным критерием. Для используемых в лабораторной работе импульсных периодических сигналов таким критерием является ограничение спектра сигнала частотой его высшей гармоники, амплитуда которой составляет 0,1 и менее от амплитуды первой гармоники, которая и принимается за максимальную частоту спектра сигнала Fm.
Для периодического двухполярного сигнала типа меандр амплитудой Um отношение амплитуд l-й гармоники Um(l)и первой гармоники Um(1) определяется как
Um(l)/Um(1) = 1/l , l = 1, 3, 5, ….
При этом амплитуда первой гармоники находится как Um(1) = (4/p)Um.
Для периодического двухполярного пилообразного сигнала амплитудой Um отношение амплитуд l-й гармоники Um(l) и первой гармоники Um(1) (по модулю) определяется как
Um(l)/Um(1) = 1/l , l = 1, 2, 3, 4, 5, ….
При этом амплитуда первой гармоники находится как Um(1) = (2/p)Um.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
