Исследование преобразований спектров при дискретизации сигналов по времени в системах ЦОС: Методические указания по выполнению лабораторной работы, страница 2

Для треугольного периодического двухполярного сигнала амплитудой U_m отношение амплитуд l-й гармоники U_m(l)и первой гармоники U_m(1) (по модулю) определяется как

U_m(l)/U_m(1)   = 1/l² , l = 1, 3, 5, ….

При этом амплитуда первой гармоники находится как U_m(1) =  (8/p²)U_m.

Для периодической последовательности однополярных прямоугольных импульсов длительностью τ_и, периодом следования Т (скважностью Q = T/τ_и) и амплитудой U_m отношение амплитуд l-й гармоники U_m(l) и первой гармоники U_m(1)  (по модулю) определяется как

U_m(l)/U_m(1)   = |sin(lp/Q)|/l|sin(p/Q)|, l = 1, 2, 3, 4, 5, ….

При этом амплитуда первой гармоники находится как U_m(1) = (2/p)U_m|sin(p/Q)|.

3.3. Преобразования частоты при дискретизации сигналов

При обработке результатов измерения спектров дискретных сигналов, получаемых дискретизацией аналоговых сигналов, содержащих составляющие с частотами F > f_д/2,  нужно найти соответствующие им частотные составляющие в основной полосе частот спектра дискретного сигнала 0–f_д/2. Для этого можно воспользоваться соотношением:

F_пр = |F – [F/f_д]_цч.окр ·f_д|,

где F_пр – значение частоты дискретного сигнала, полученное путем преобразования частоты  аналогового сигнала F  при его дискретизации. Индекс «ц.ч.окр» означает целую часть числа, заключенного в прямых скобках, взятую с округлением.

            Примеры определения частотных составляющих дискретного сигнала.

При f_д = 8000 Гц, F = 4250 Гц получаем: [F/f_д]_цч.окр = 1, F_пр = 3750 Гц.

При f_д = 10000 Гц, F = 15250 Гц получаем: [F/f_д]_цч.окр = 2, F_пр = 4750 Гц.

При f_д = 12000 Гц, F = 11250 Гц получаем: [F/f_д]_цч.окр = 1, F_пр = 750 Гц.

3.4. Соотношения, используемые программой, для измерения амплитуды (размаха), среднего, эффективного значения и стандартного отклонения сигнала

По измеренной осциллограмме сигнала x(n) программа вычисляет и выводит на цифровые индикаторы параметры сигнала:

размах (удвоенная амплитуда) U_pp;  ­

среднее значение (постоянная составляющая или смещение нуля) U₀;

эффективное значение U_эфф;

стандартное (среднеквадратическое) отклонение U_ско.

Они определяются в соответствии со следующими соотношениями:

      

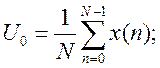
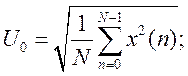
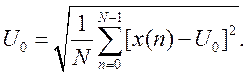
Точность оценки параметров сигнала возрастает с увеличением длины реализации N, по которой они вычисляются.

В соответствии с теоремой Парсеваля эффективное и среднеквадратическое значения сигнала (стандартное отклонение) можно найти также и по его спектру:

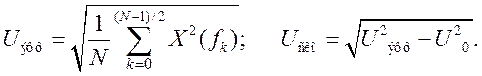
Среднее значение сигнала (постоянное смещение) соответствует в частотной области значению его нулевой частотной выборки: 

3.5. Определение мощности и среднеквадратического значения аналогового и дискретного шума

 3.6. Определение эффективной частоты дискретизации периодического сигнала в режиме строб-преобразования

Режим стробоскопического преобразования реализуется при числе периодов сигнала на длине реализации р, большем единицы: р > 1. При этом частоты сигнала и дискретизации связаны между собой соотношением: F = (f_д /N)р, в котором N  (длина реализации сигнала) и р являются взаимно простыми целыми числами. Считанная реализация периодического сигнала при строб-преобразовании представляется на осциллограмме своим одним периодом с числом выборок N. Это эквивалентно дискретизации сигнала на интервале, равном одному периоду, с эффективной частотой дискретизации  f_д.эфф = N×F. Значение N  при реализации режима строб-преобразования определяется автоматически и отображается на индикаторе длины реализации панели настройки АЦП при переключении режима пуска АЦП со строб-преобразования на режим «От синтезатора». Значение f_д.эфф  можно  определить также по графику спектра сигнала, измеренному в режиме строб-преобразования, который изображается в полосе частот (0– f_д.эфф /2).

4. Исходные данные к лабораторной работе

Лабораторная работа выполняется по индивидуальным исходным данным. Варианты исходных данных отличаются значениями частоты периодических сигналов F_i и номинальной частоты дискретизации f_д.н, которые выбираются из приводимой ниже таблицы.

Таблица 1

Группа	Частота сигнала Fi , Гц	Частота дискре-тизации fд.н , Гц	Номер варианта
Р53-1	200 + i×400	10000	i = 1, 2, … 12
Р53-2	80 + i×80	8000	i = 1, 2, … 24
Р53-3	100 + i×200	10000	i = 1, 2, … 16
Р53-4	250 + i×250	10000	i = 1, 2, … 12
Р53-6б	120 + i×480	8000	i = 1, 2, … 6
Р23-1	50 + i×50	8000	i = 1, 2, … 20

Номер индивидуального варианта определяется порядковым номером студента в списке группы.

 5. Описание аппаратно-программного комплекса

Полное описание АПК АРМЭКС приведено в документе Word «Руководство пользователя АРМЭКС». Ниже даются основные сведения об АПК, необходимые для выполнения работы.

5.1. Состав аппаратно-программного комплекса

АПК с удаленным доступом АРМЭКС состоит из клиентской и серверной части.

 Клиентскую часть образует сетевое программное обеспечение (ПО), осуществляющее взаимодействие клиента с сервером, и измерительное ПО, осуществляющее подготовку данных для сервера и обработку измерительных данных, получаемых с сервера. С помощью измерительного ПО клиента реализуются функции измерительных приборов – осциллографа, анализатора спектра, измерителя АЧХ и ФЧХ, а также синтезируются сигналы, которые передаются в серверную часть АПК.

Серверная часть АПК содержит аппаратный измерительный блок и серверное программное обеспечение, управляющее измерениями и сетевым обменом.

В данной лабораторной работе используются аппаратные и программные средства АПК, включающие синтезатор аналоговых сигналов, устройство ввода сигналов в ПК, осциллограф и анализатор спектра.