#############################################################################
1.14. Как определяются передаточная функция и ИХ РЦФ при каскадной форме реализации через передаточные функции и ИХ биквадратных звеньев?
2.14. Как найти значения нулей биквадратного звена по его коэффициентам?
3.14. Из каких условий выбирается вид аппроксимирующей функции?
4.14. Покажите граф-схему алгоритма программной реализации РЦФ для каскадной формы его реализации.
#############################################################################
1.14. Какой возможен порядок операций по ограничению разрядности произведений и сумм произведений в звене РФ второго порядка при прямой форме его реализации?
#############################################################################
2.14. Как можно выполнить масштабирование сигнала путем масштабирования
коэффициентов звеньев РФ?
#############################################################################
3.14. Что такое шум (погрешность) квантования, оценки погрешности квантования чисел?
1.14.
каскадная форма реализации рекурсивных фильтров
Передаточная функция каскадно реализуемогоРФ
(рис. 2.8) определяется произведением передаточных функций его звеньев: 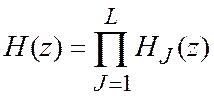 ,
,
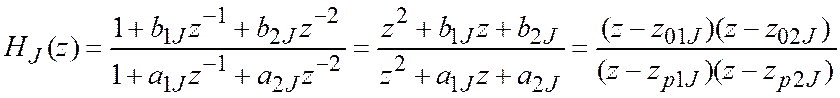 , (2.56)
, (2.56)
где HJ(z)-передаточная функция J-го биквадратного звена при значении коэффициента b0J = 1; при b0J ¹ 1 добавляется общий нормирующий или масштабирующий множитель С0.
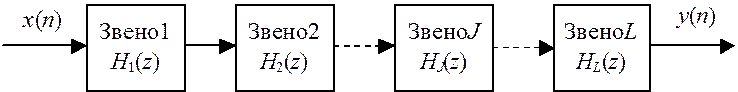
Рис. 2.8. Каскадная структура ЦФ
Для звена первого порядка коэффициенты b2J и a2J в (2.56) равны нулю.
Входным сигналом J-го звена xJ(n) в такой структуре является выходной сигнал yJ–1(n) предыдущего (J-1)-го звена: xJ(n) = yJ–1(n).
Коэффициенты звеньев и их полюсы и нули связаны соотношениями:
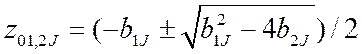 ;
; 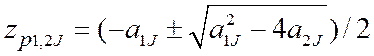 ;
;
b1J = - (z01J + z02J); a1J = - (zp1J + zp2J);
b2J = z01J z02J; a2J = zp1J zp2J. (2.57 )
Пары нулей и полюсов, определяющие значения
коэффициентов J-го звена, могут быть вещественными разными,
вещественными равными, а при ![]() и
и ![]() -
комплексно-сопряженными:
-
комплексно-сопряженными:
z0(p)1J = z*0(p)2J = z0(p)J.
В этом случае соотношения (2.57) принимают вид
![]() ,
, 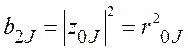 ,
,
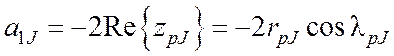 ,
,
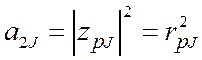 , (2.58)
, (2.58)
где
![]() -
нормированная частота нуля или полюса.
-
нормированная частота нуля или полюса.
Для
звена первого порядка ![]()
2.14.
Значениям нулей и полюсов z01 = 1, z02 = -1, zp1 = 0,4 + j0,6, zp2 = 0,4 - –j0,6, графически отображенным на рис. 2.7, соответствуют следующие значения коэффициентов рекурсивного звена 2-го порядка: b0 = 1, b1 = 0, b2 = -1, a1 = - 0,8, a2 = 0,52.
Частотная характеристика H(jw) каскадно реализуемого фильтра также определяется произведением частотных характеристик его звеньевHJ(jw):
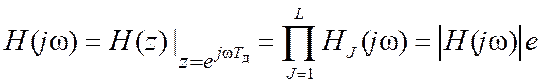 jj(w).
jj(w).
Ее модуль |H(jw)| (АЧХ фильтра) и аргумент j(w) (ФЧХ фильтра) соответственно равны
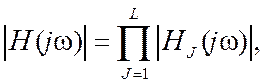 j(w) =
j(w) = ![]() jJ(w).
jJ(w).
Выражения
для частотной (HJ(jl)), амплитудно-частотной (|HJ(jl)|) и фазочастотной (jJ(l)) характеристик звеньев,
представленные функцией нормированной
цифровой частоты ![]() , имеют вид:
, имеют вид:
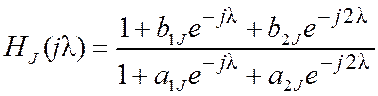 ,
,
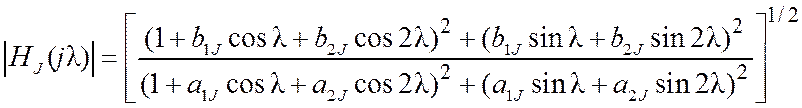 ,
,
jJ(l) 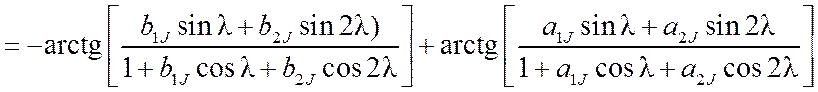 .
.
3.14.
Синтез РФ включает следующие этапы:
1. На основе исходных данных на синтез ЦФ (граничных частот fc , fз , (lс, lз) и допусков на погрешности аппроксимации АЧХ ап,, аз) определяются исходные данные на синтез АФПНЧ, задающие требования к его АЧХ: допуски на погрешности аппроксимации ап,, аз – те же, что и для ЦФ, и граничные частоты Wc =1 и Wз =fоб(lз),получаемые с помощью частотных преобразующих функций W =fоб(l) табл. 3.1.
2. По значениям ап,, аз и Wз синтезируется АФПНЧ: выбирается тип аппроксимирующей функции, определяются порядок фильтра m и значения его полюсов и нулей: ppi, p0i, i = 1, 2, ... m. От вида аппроксимации зависит порядок фильтра и, как следствие, сложность его реализации и быстродействие. Наименьший порядок имеют эллиптические фильтры, наибольший – фильтры Баттерворта и Бесселя. В то же время фильтры с полиномиальной аппроксимацией (Баттерворта, Бесселя, Чебышева инверсная) имеют коэффициенты b1, b2 передаточной функции звеньев каскадной реализации, равные 0, ±1, ±2, умножение на которые выполняется тривиально. В результате при большем порядке требуемый объем вычислений при их реализации может оказаться меньше, чем для ЦФ с дробной аппроксимацией (Золотарева–Кауэра, Чебышева прямая), где коэффициенты b1, b2 не являются тривиальными. Кроме того, при выборе вида аппроксимации учитываются дополнительные требования к АЧХ, например, ее желаемая монотонность в полосе пропускания и или полосе задерживания, а также к ФЧХ – необходимая степень линейности ФЧХ в полосе пропускания.
4.14.
граф-схемы алгоритмов программной реализации рекурсивных фильтров
Под программной реализацией ЦОС понимается обработка, выполняемая на компьютере не в реальном времени, например, обработка записей сигналов. Обработка в реальном времени требует дополнительных аппаратно-программных средств синхронизации ввода, обработки и вывода данных, которые рассматриваются в главе 12.
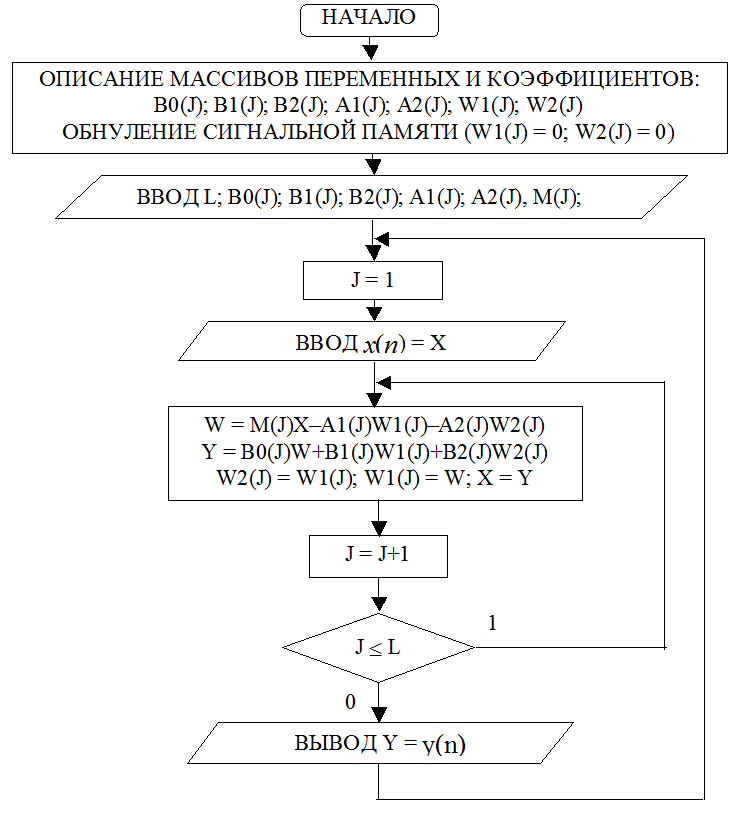
На рис. 2.13, 2.14 приведены граф-схемы алгоритмов (ГСА) программной реализации РФ на основе каскадного и параллельного соединения канонических биквадратных звеньев.
Программы ЦФ имеют циклическую структуру. Во внутреннем цикле по переменной J (номер звена) осуществляется последовательная обработка текущего отсчета сигнала биквадратными звеньями фильтра в соответствии с их базовой операцией. Базовая операция включает разностные уравнения звена (2.64) и операторы присваивания или пересылки (сдвига) сигнальной памяти wJ(n-2) = wJ(n- 1),wJ(n-1) = wJ(n), которые предшествуют обработке следующего отсчета сигнала в соответствии с внешним циклом ГСА.
На ГСА внутренние сигналы фильтра wJ(n), wJ(n-1), wJ(n-2)представлены соответствующими программными переменными W, W1(J), W2(J). Также использованы программные переменные (идентификаторы) B0(J),B1(J), B2(J), A1(J), A2(J) для коэффициентов звеньев b0J, b1J , b2J, B0J,, B1J, a1J, a2Jи X, Y – для отсчетов сигнала x(n), y(n). Оператор X = Y присваивает значение выходного отсчета J–го звена входному отсчету (J + 1)-го, т. е. следующего звена фильтра. C помощью коэффициентов M(J) < 1 осуществляется масштабирование входных сигналов звеньев в каскадной структуре, а с помощью коэффициента М – входного сигнала всего фильтра в параллельной структуре (см. гл. 4).
1.14.
прямая форма реализации биквадратного звена
Прямая форма реализации биквадратного звена описывается разностным уравнением вида
![]() . (2.63)
. (2.63)
Ему соответствует структурная схема звена рис. 2.10, содержащая элементы памяти (задержки) z–1 на один период дискретизации Тд, умножители (Х) и сумматор å.
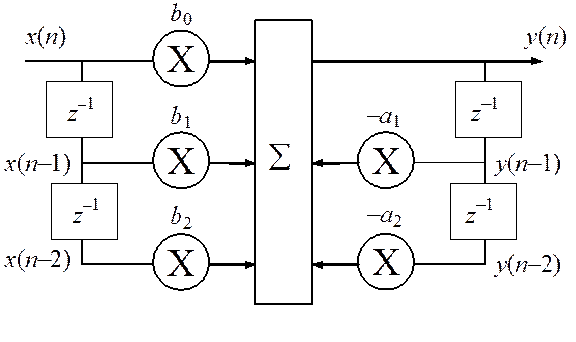
В ячейках памяти z–1, называемой сигнальной памятью фильтра, сохраняются предыдущие отсчеты входного и выходного сигналов x(n – 1), x(n –2), y(n – 1), y(n – 2). В уравнении (2.63) полагается, что x(–1) = x(–2) = y(–1) = = y(–2) = 0, что соответствует нулевым начальным условиям работы звена. Начальные условия обеспечиваются обнулением ячеек памяти z–1 до начала обработки. После обработки очередного отсчета сигнала звено должно быть подготовлено к обработке следующего. Подготовка включает операции сдвига сигнальной памяти, соответствующие операторам пересылки x(n – 1) ® x(n – 2), x(n) ® x(n – 1), y(n –1) ® y(n – 2), y(n) ® y(n – 1), или программного присваивания: x(n – 2) = x(n – 1), x(n – 1) = x(n), y(n – 2) = y(n – 1), y(n – 1) = = y(n). После выполнения их на вход звена может быть подан следующий отсчета сигнала.
Уравнению звена (2.63) эквивалентна также пара
разностных уравнений вида ![]() ,
,
![]() ,
,
которые раздельно описывают нерекурсивную и рекурсивную части звена при прямой форме его реализации.
Для аппаратной реализации звена необходимы 4 элемента
памяти, сумматор на 5 входов и 5 (4 при b0 = 1) умножителей.
При программной реализации нужно выполнить 5 (4) операций умножения и 4
операции сложения на 1 отсчет сигнала.
2.14.
Масштабирование сигналов в цифровых фильтрах используют для исключения возможного переполнения сумматоров при накоплении сумм произведений и осуществляют введением масштабных умножителей на входе всего фильтра (рис. 4.2, а) или входах его звеньев в случае каскадной реализации (рис. 4.2, б).
Масштабные множители (ММ) mi выбирают так, чтобы амплитуды сигналов на выходах сумматоров или звеньев vi(n) (рис. 4.3) при максимальном значении сигнала на входе фильтра x(n), равном единице (|x(n)|max= 1), не превышали по модулю некоторого максимального значения, принимаемого также обычно за единицу (|vi(n)|max= 1).
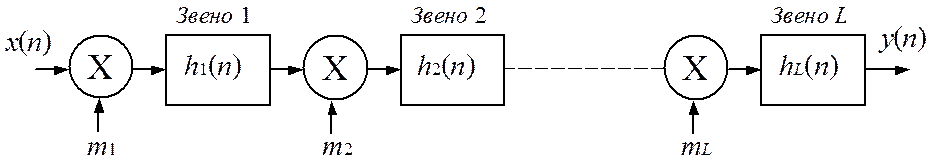
3.14.
Ограничение разрядности чисел называется их квантованием. Очевидно, что квантование произведений или сумм произведений эквивалентно умножению с конечной точностью и приводит к погрешности обработки. Эту погрешность аналогично погрешности квантования АЦП называют шумом квантования или собственным шумом цифрового фильтра
ОЦЕНКИ ПОГРЕШНОСТИ КВАНТОВАНИЯ ЧИСЕЛ
Вызываемую ограничением разрядности чисел погрешность
квантования, определяют разностью их квантованного и точного
значений: e(n) = vкв(n)-v(n). Полагается,
что значения погрешности или отсчеты шума квантования e(n)равновероятны
в пределах ![]() при усечении и
при усечении и ![]() при округлении и характеризуются
максимальным значением
при округлении и характеризуются
максимальным значением ![]() , дисперсией
, дисперсией 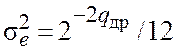 и среднеквадратичным значением
(СКЗ)
и среднеквадратичным значением
(СКЗ) ![]() , где h = 1при усечении
и ½ при округлении; qдр- число сохраняемых разрядов дробной части числа;
, где h = 1при усечении
и ½ при округлении; qдр- число сохраняемых разрядов дробной части числа; ![]() – вес единицы младшего разряда числа
(ЕМР).
– вес единицы младшего разряда числа
(ЕМР).
Для цифрового сигнала АЦП qдр = qx - определяется числом разрядов АЦП без учета знакового разряда.
Для внутренних сигналов фильтра, получаемых в результате умножения и накопления сумм произведений и приведения их к формату правильной дроби, qдр равно числу разрядов qR сигнальных регистров фильтра (также без учета знакового разряда) или иначе длине слова фильтра.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.