Исследование методов спектрального анализа сигналов на основе дискретного преобразования Фурье: Лабораторная работа № 4.2

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

КРАСНОЯРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Институт радиоэлектроники

Лабораторная работа по ЦОС № 4.2

исследование методов спектрального анализа сигналов на основе дпф

выполнил: студент гр. Р52-4

Титов Ю.С.

проверил:

Глинченко А.С.

Красноярск 2006

Цели:

- освоить методику анализа и изучить параметры и характеристики анализаторов амплитудного и фазового спектров сигналов на основе ДПФ.

- изучить, как осуществляется анализ энергетических спектров (спектральной плотности мощности) дискретных случайных сигналов с помощью ДПФ методом периодограмм.

Исходные данные:

- тип фильтра – полосно-пропускающий (ППФ);

- центральная частота полосы пропускания f_0i=1000Гц;

- нижняя частота среза f_c1=900Гц;

- верхняя частота среза f_c2=1100Гц;

- нижняя частота задерживания f_з1=800Гц;

- верхняя частота задерживания f_з2=1200Гц;

- допустимая неравномерность АЧХ в полосе пропускания а_п<6дБ;

- затухание АЧХ в полосе задерживания а_з>46дБ;

- частота дискретизации f_д=4000Гц.

Ход работы:

Для лабораторной работы синтезирован нерекурсивный ЦФ, имеющий порядок=81.

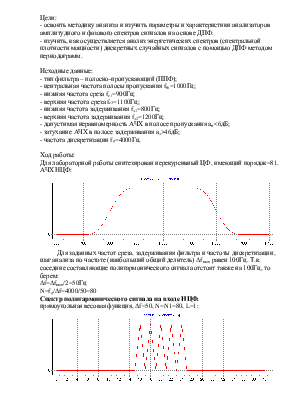
АЧХ НЦФ:

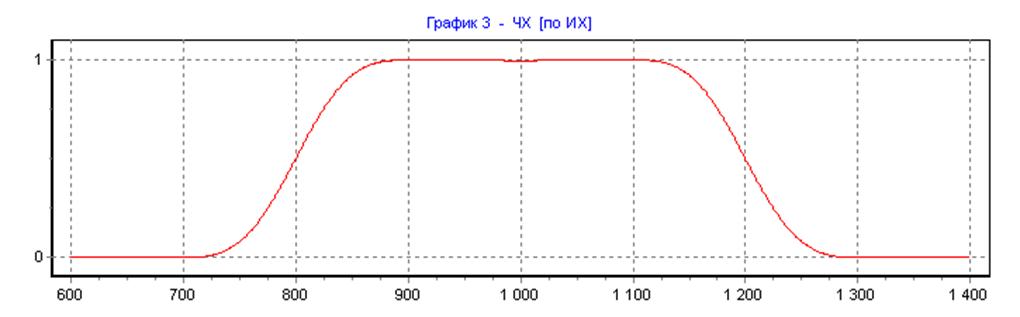
          Для заданных частот среза, задерживания фильтра и частоты дискретизации, шаг анализа по частоте (наибольший общий делитель) ∆f_max равен 100Гц. Т.к. соседние составляющие полигармонического сигнала отстоят также на 100Гц, то берем:

∆f=∆f_max/2=50Гц

N=f_д/∆f=4000/50=80

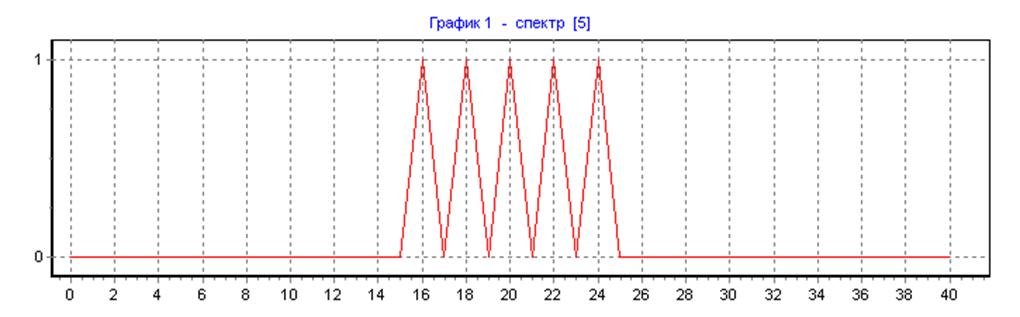
Спектр полигармонического сигнала на входе НЦФ.

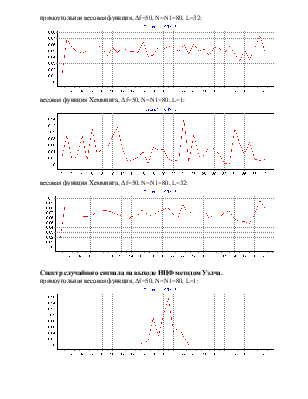
прямоугольная весовая функция, ∆f=50, N=N1=80, L=1:

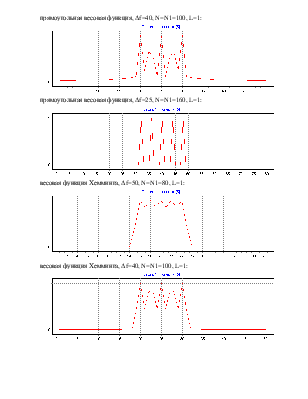
прямоугольная весовая функция, ∆f=40, N=N1=100, L=1:

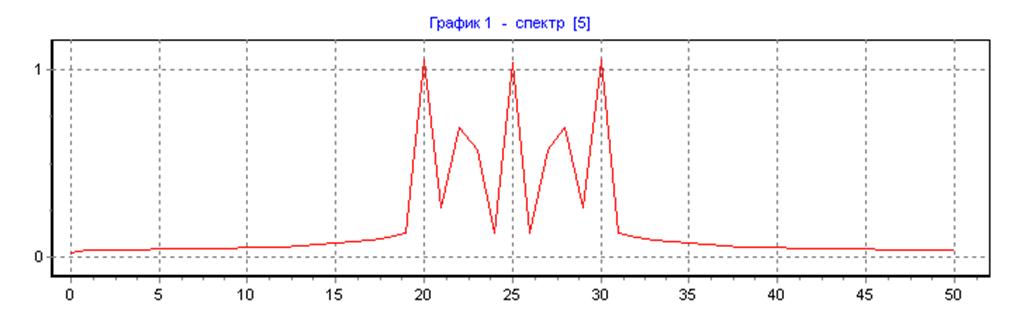
прямоугольная весовая функция, ∆f=25, N=N1=160, L=1:

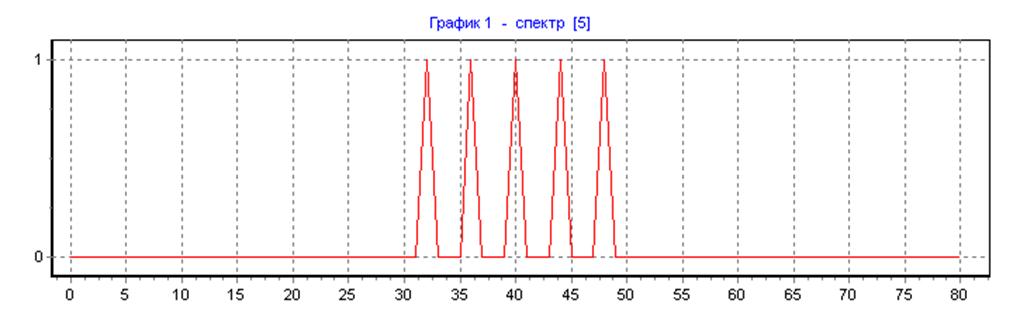
весовая функция Хемминга, ∆f=50, N=N1=80, L=1:

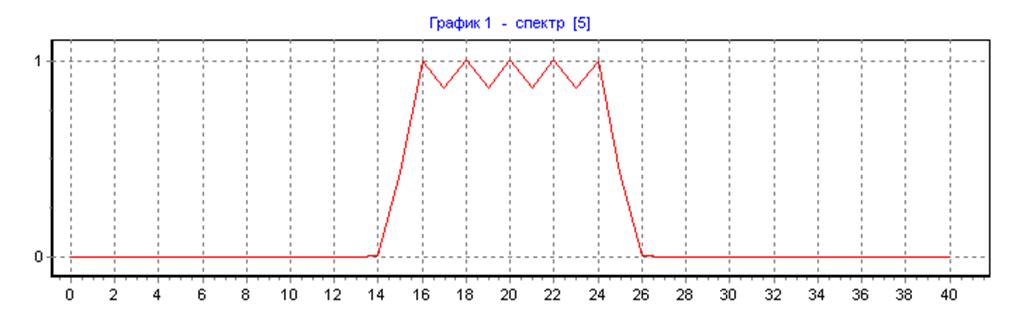
весовая функция Хемминга, ∆f=40, N=N1=100, L=1:

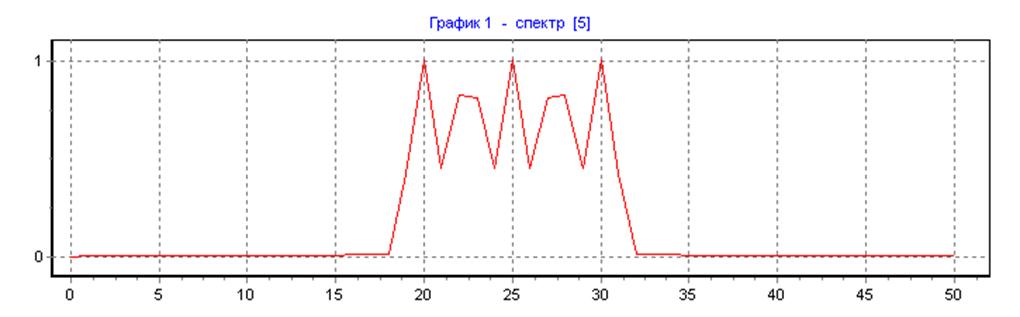
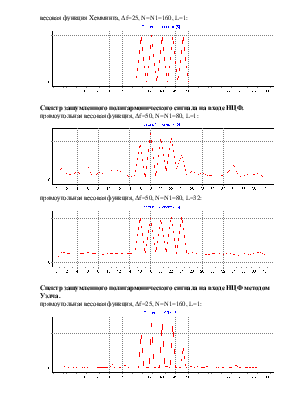
весовая функция Хемминга, ∆f=25, N=N1=160, L=1:

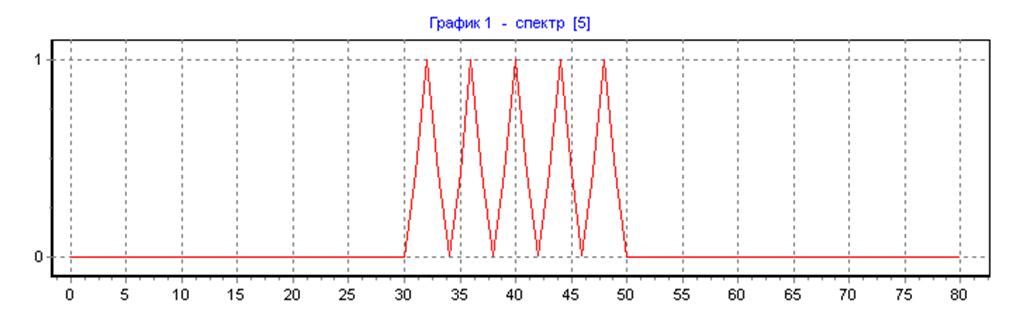
Спектр зашумленного полигармонического сигнала на входе НЦФ.

прямоугольная весовая функция, ∆f=50, N=N1=80, L=1:

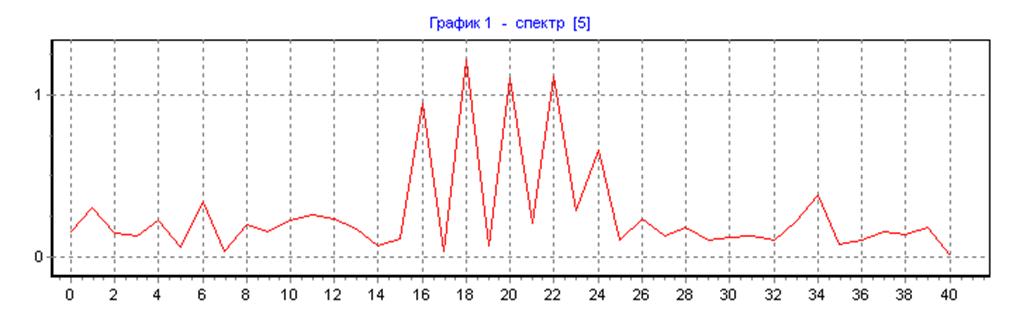
прямоугольная весовая функция, ∆f=50, N=N1=80, L=32:

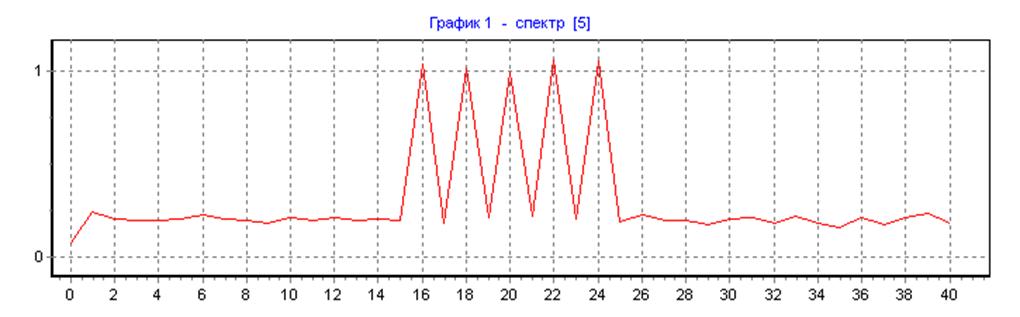
Спектр зашумленного полигармонического сигнала на входе НЦФ методом Уэлча.

прямоугольная весовая функция, ∆f=25, N=N1=160, L=1:

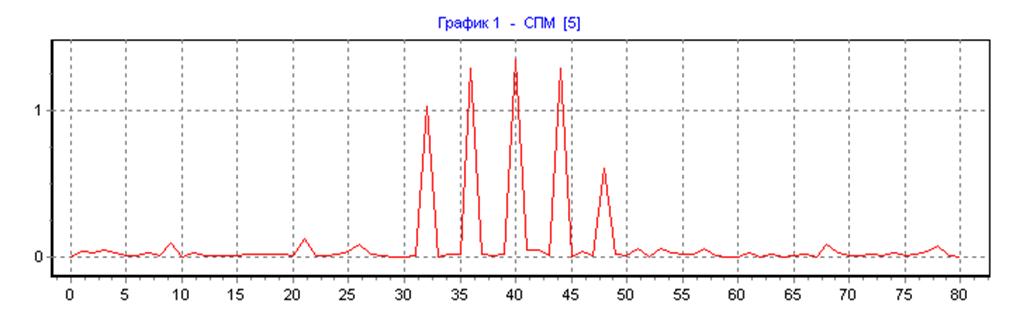
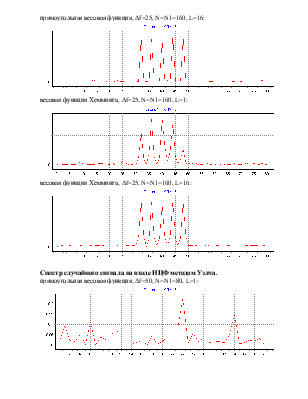
прямоугольная весовая функция, ∆f=25, N=N1=160, L=16:

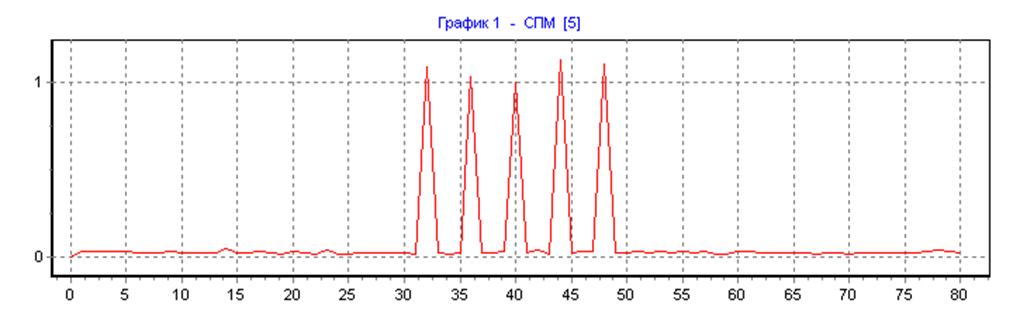
весовая функция Хемминга, ∆f=25, N=N1=160, L=1:

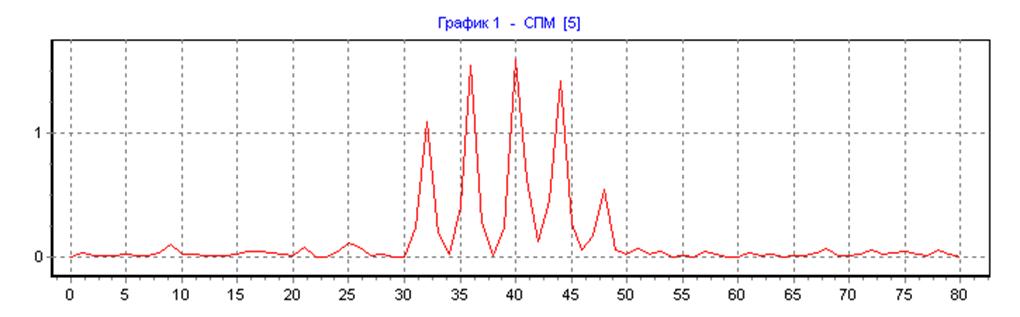
весовая функция Хемминга, ∆f=25, N=N1=160, L=16:

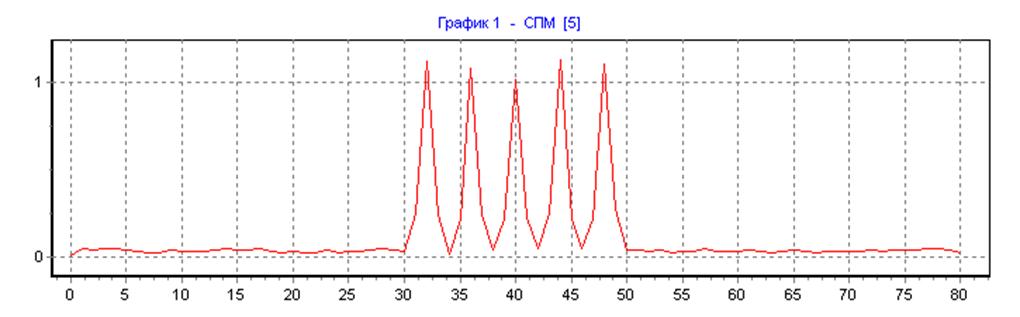
Спектр случайного сигнала на входе НЦФ методом Уэлча.

прямоугольная весовая функция, ∆f=50, N=N1=80, L=1:

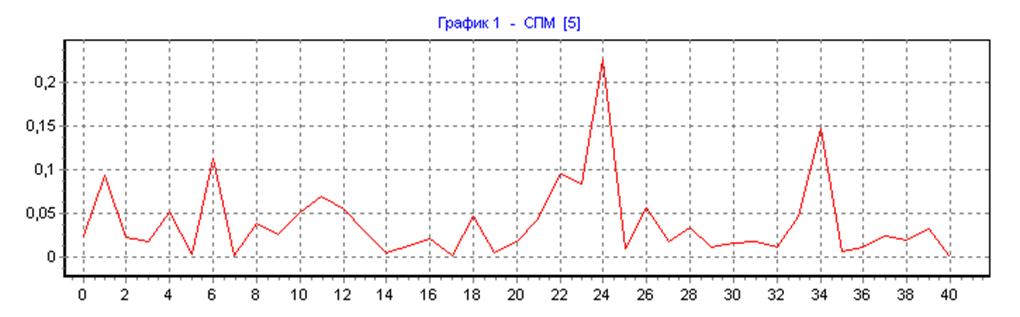
прямоугольная весовая функция, ∆f=50, N=N1=80, L=32:

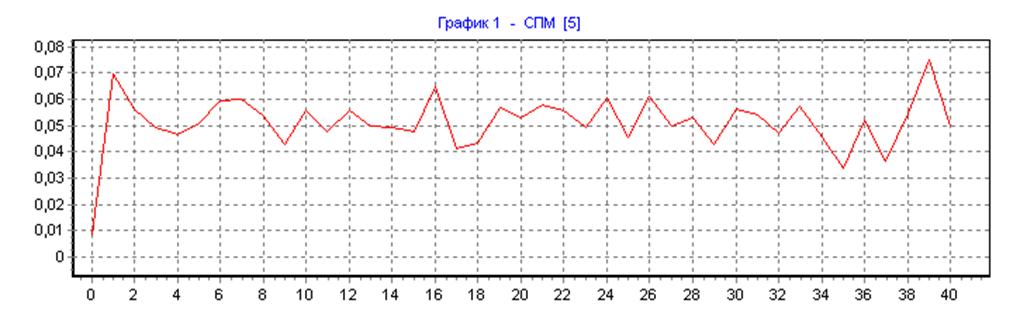
весовая функция Хемминга, ∆f=50, N=N1=80, L=1:

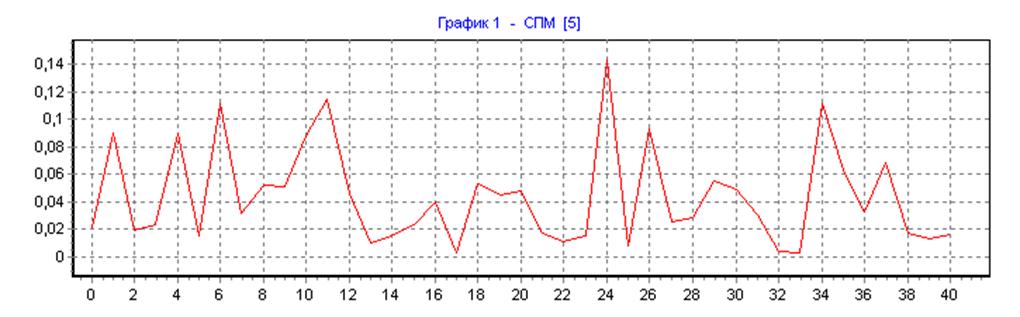
весовая функция Хемминга, ∆f=50, N=N1=80, L=32:

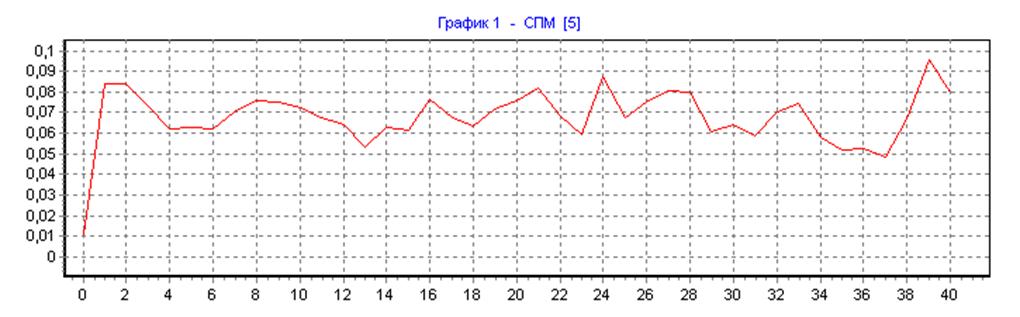
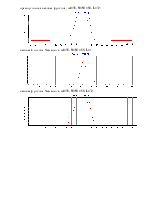
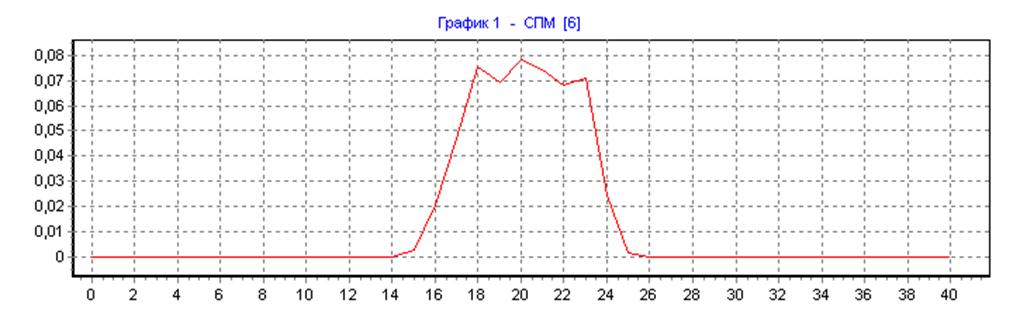
Спектр случайного сигнала на выходе НЦФ методом Уэлча.

прямоугольная весовая функция, ∆f=50, N=N1=80, L=1:

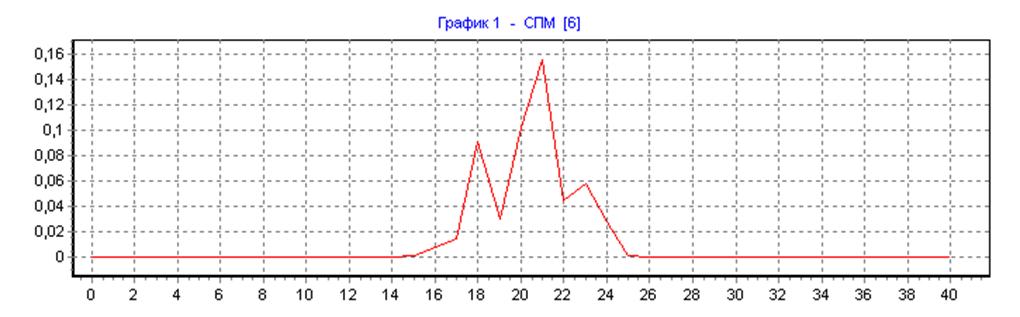
прямоугольная весовая функция, ∆f=50, N=N1=80, L=32:

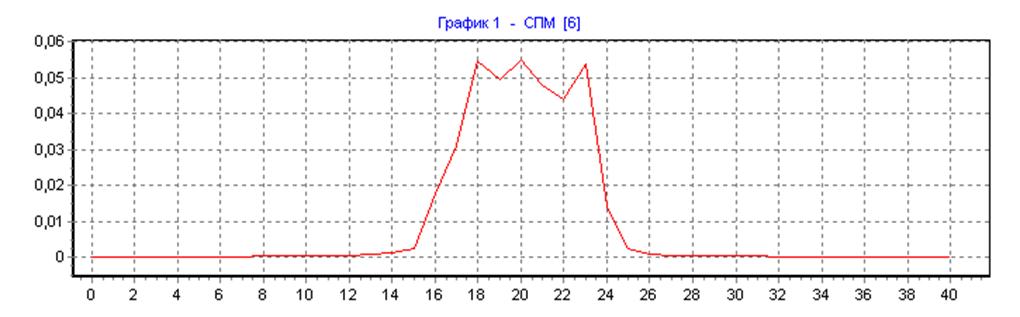
весовая функция Хемминга, ∆f=50, N=N1=80, L=1:

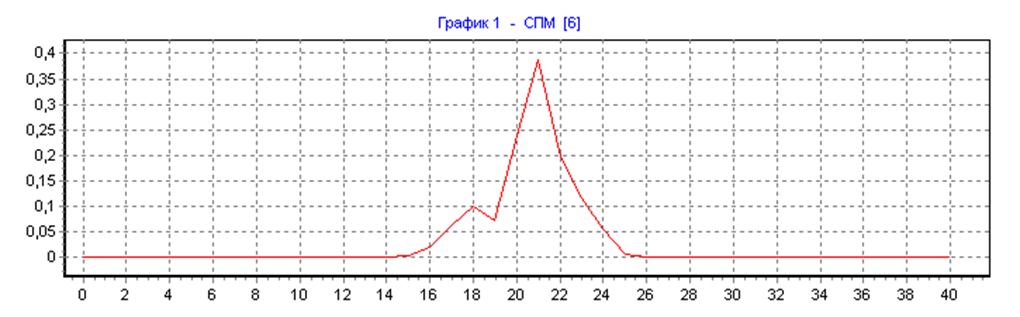
весовая функция Хемминга, ∆f=50, N=N1=80, L=32: