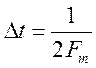Исследование и разработка акустического дефектоскопа на основе метода свободных колебаний (Квалификационная работа бакалавра), страница 7

                                                                ,                      (11)                                                                      

где- максимальная частота сигнала, подвергающаяся анализу.

Она определяется из требований ТЗ и из частот свободных колебаний ОК. В идеале, она должна быть верхней частотой подавления входного полосового фильтра.

Следующий шаг – нормировка шкалы АЦП к оперируемым процессором величинам. Этот шаг обязателен из-за возможности появления переполнения при вычислении ДПФ. Далее  пронормированный вектор подвергается дискретному преобразованию Фурье. Рассмотрим этот вопрос более подробно. В результате применения ДПФ к вещественному вектору  получаем комплексный  вектор той же длины  через следующее выражение:

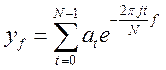                                                                            (12)

В данном рассуждении под длиной вектора понимается число его координат, а не евклидова норма. Существует также обратное преобразование Фурье (операция, обратная только что описанной), но здесь оно рассматриваться не будет ввиду его отсутствия в алгоритме.

Непосредственное вычисление координат результирующего вектора через (12) приводит к 2N операциям на каждый коэффициент . Т.к. всего мы имеем N  коэффициентов, то общая сложность алгоритма составляет , что не представляет практического интереса из-за необходимости реализации данного алгоритма на МК и следующей отсюда низкой скорости вычислений. В таких случаях применяют быстрое преобразование Фурье, которое характеризуется значительно меньшим объемом операций на вычисление одной компоненты результирующего вектора.

Будем использовать алгоритмы с основанием 2, использующиеся, когда число входных отсчетов равно . Основная идея, лежащая в их основе, заключается в сведении вычисления N-точечного БПФ к вычислению нескольких -точечных ДПФ при .

Выражение (12) можно также переписать как

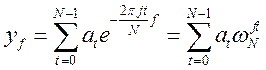                                                    ,          (13)

где 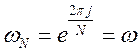.  здесь – главный комплексный корень N-степени из единицы. В некоторых случаях индекс N будет опускаться, что будет означать степень корня, равную длине преобразуемого вектора.

В итоге, идею БПФ можно записать так

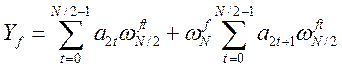                                              ,    (14)

что соответствует разбиению искомой последовательности на две подпоследовательности соответственно четных и нечетных отсчетов входного сигнала. В свою очередь, каждую из подпоследовательностей длины N/2 можно представить двумя подпоследовательностями длиной N/4 и так далее, пока не останутся 2-х точечные. Всего таких ступеней преобразования  . Сложность алгоритма слияния на каждой ступени равна . Умножая на число ступеней, получаем сложность всего алгоритма равную . Такой алгоритм БПФ использует прореживание по времени, разделяя вектор входного сигнала на четные и нечетные компоненты.

Вышеописанный алгоритм используется в данной работе как базовый алгоритм для вычисления ДПФ. Блок-схема данного алгоритма приведена в приложении Б.

4.2 Статистическая нормировка

Далее выполняется статистическая нормировка полученных после БПФ модулей гармоник сигнала, в соответствие с выражением (15)

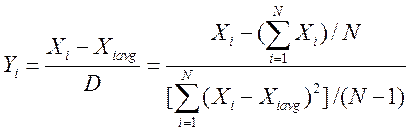                                         ,                                                                    (15)                               

где     - длина вектора модулей гармоник;

          - модуль гармоники i;

          - среднее арифметическое входного вектора.

В результате применения (15) к исходному вектору действительных величин X получаем вектор действительных величин Y со следующими параметрами (16)

                                                         ,               (16)                                                                                                          

где

D – дисперсия;

M – математическое ожидание.

Необходимость данной нормировки обосновывается требованием к представлению обучающих выборок для нейроэмулятора «Модели», который будет описан далее в части «выбор нейроэмулятора».

4.3 Нейронная сеть

Будем использовать нейронную сеть (НС) со структурой, показанной на рисунке 8.

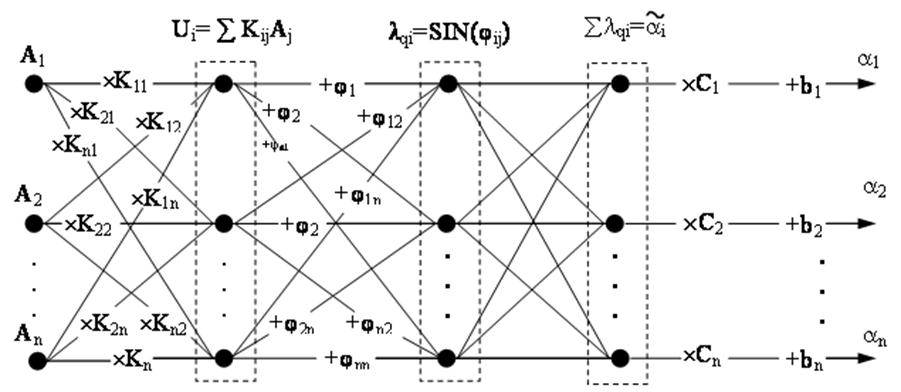
Рисунок 8 - Структура используемой НС

Как показано в /7/, такая структура НС называется персептроном, используемым для распознавания образов. Функционирование такой НС описывается выражением (17) (запись для однослойного персептрона).

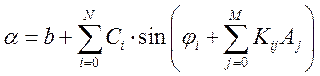                                                ,      (17)                                                                      

где     N – число нейронов;

M – число входов;

A – вектор входных данных;

K – матрица синаптических коэффициентов;

C – вектор коэффициентов взвешенного суммирования выходов нейронов;

 – вектор начальных состояний нейронов;

b – постоянная составляющая выхода.

Выходом данной НС является вещественное число.

Стоит отметить, что разработанные исходные коды приведены в приложении В.

5 Выбор средств реализации

5.1 Программные средства работы с МК

Перед рассмотрением вопроса выбора МК рассмотрим иерархию программных средств работы с МК, что необходимо для дальнейшего понимания материала, посвященного тестовым задачам МК.

На рисунке 9 представлена иерархия программных средств работы с МК.

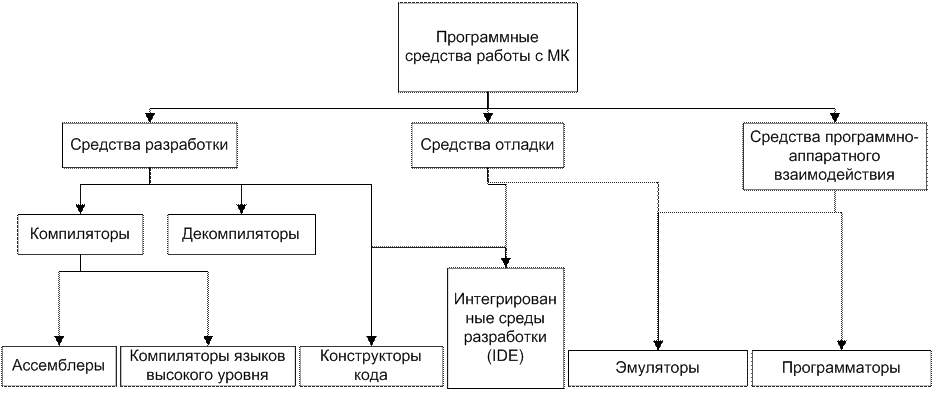
Рисунок 9 - Иерархия программных средств работы с МК

Как видно из диаграммы, программные средства работы с МК подразделяются на средства разработки, средства отладки, и средства аппаратно-программного взаимодействия.

- Средства разработки предназначены непосредственно для написания программ. Сюда входят компиляторы ассемблера и языков высокого уровня, декомпиляторы (программные средства, позволяющие получить ассемблерный листинг или код на высокоуровневом языке программирования, имея бинарный файл прошивки МК), а также интегрированные среды разработки (IDE – Integrated Development Environment), представляющие собой многокомпонентные приложения, совмещающие компиляторы (как ассемблера, так и высокого уровня),  средства редактирования и контроля исходных текстов, декомпиляторы, средства отладки – т.е. весь комплекс прикладных программ в процессе разработки. Поэтому IDE относят к средствам отладки и средствам разработки.