Исследование и разработка акустического дефектоскопа на основе метода свободных колебаний (Квалификационная работа бакалавра), страница 3

Задача определения коэффициента формы решается на основании известных работ по теории колебаний /12, 13, 14/. Таким образом, зная коэффициент формы для конкретного изделия, можно по частоте свободных колебаний рассчитать требуемый параметр.

Сложность данного метода заключается в том, для любого ОК может быть определено несколько частот свободных колебаний, соответствующих нескольким типам колебаний (продольных, поперечных, крутильных, изгибных и т.д.), т.е. различным модам этих колебаний. Набор этих частот образует резонансный спектр изделия, и при определении частоты свободных колебаний необходимо производить опознание нужной моды колебаний в общем резонансном спектре /10/, что является непростой задачей. К примеру, спектр частот собственных колебаний шлифовального круга ПП 200х25х80 имеет вид, как показано на рисунке 2:

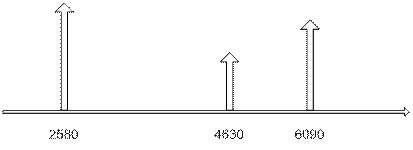
Рисунок 2 - Спектр частот собственных колебаний шлифовального круга ПП 200х25х80

Для изделий простой формы удается решить задачу выделения из резонансного спектра конкретного типа колебаний путем определенного расположения опор и приемоизлучающей системы относительно ОК. В том случае, если данная методика невозможна, приходится решать задачу опознания составляющих частотного спектра.

Число методов определения частот свободных колебаний достаточно велико, здесь мы попробуем дать лишь упрощенную классификацию (см. рисунок 3). Статические методы подразумевают вычисление частоты свободных колебаний для каждого конкретного типа изделия на основе теории колебаний.

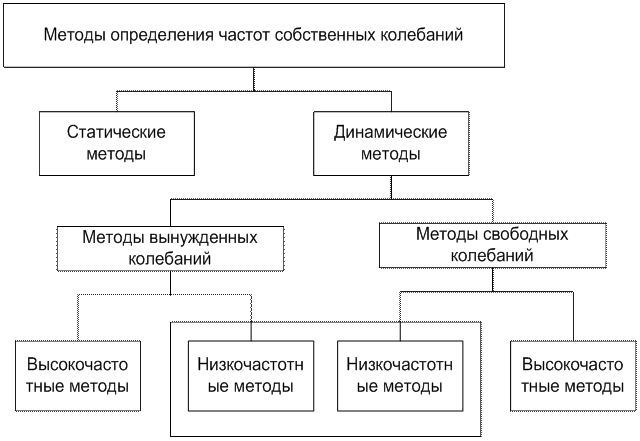
Рисунок 3 - Классификация методов определения  частот собственных колебаний

В настоящее время существует большое число различных устройств и установок для определения частот свободных колебаний изделий различных форм и размеров. Сущность методов, положенных в основу этих устройств, сводится в возбуждении в ОК колебаний, частота которых совпадает с частотой собственных колебаний и регистрации значения этой частоты. По способу возбуждения и регистрации колебаний в изделии эти методы могут быть разделены на методы свободных и вынужденных колебаний.

Сущность метода свободных колебаний заключается в воздействии на ОК какой-либо силы, обеспечивающей возбуждение в нем колебаний в широком диапазоне частот, и регистрации колебаний после снятия возбуждающей силы и установлении частоты свободных колебаний. В качестве подобной вынуждающей силы наиболее широкое применение находит механический удар, возбуждающий в ОК колебания в достаточно широком диапазоне частот. На рисунке 4 приведена блок-схема метода свободных колебаний.

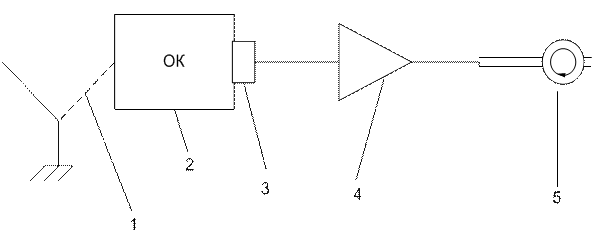
Рисунок 4 - Блок-схема метода свободных колебаний

Работа устройства, реализующего данную схему, заключается в следующем: при нанесении удара ударником 1 по объекту контроля 2 в последнем возникают механические колебания в широком диапазоне частот, которые преобразуются в электрические приемником 3, затем усиливаются усилителем-синхронизатором 4 и попадают на измеритель частоты 5, который, собственно, и показывает частоту собственных колебаний ОК. Усилитель-синхронизатор включает в себя фильтр, обеспечивающий подавление колебаний переходного процесса, в результате чего на измеритель частоты попадают колебания как раз после установления собственных колебаний изделия.

Очевидно, что одной из самых сложных деталей вышеописанного устройства является именно усилитель-синхронизатор, а точнее, его фильтр, поскольку существует влияние колебательного процесса на результаты измерений. При неправильном выборе параметров удара и момента начала измерений погрешности при измерениях могут достигать значительной величины и препятствовать применению МСК на практике. Резюмируя, можно сказать, что вопросы определения параметров колебательного процесса, возникающего в ОК при возбуждении в последнем колебаний с помощью удара – важнейшая часть МСК. Далее рассмотрим модель колебательного процесса в ОК.

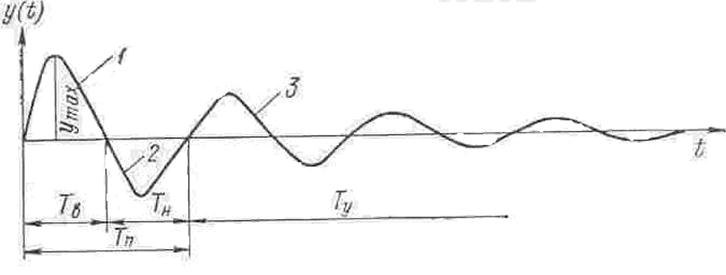
Рисунок 5 - Модель колебательного процесса в ОК

На рисунке 5 изображена модель колебательного процесса, возбужденного в ОК при использовании МСК. Весь процесс может быть разбит на 3 участка: 1 – вынужденные колебания, вызванные внешним воздействием (ударом), 2 – переходной процесс от вынужденных колебаний к собственным колебаниям ОК, 3 – установившиеся колебания, как правило, затухающие по экспоненциальному закону синусоидальные колебания вида

                                                      .              (2)

        Под временем переходного процесса при решении данной задачи понимают

                                                             ,                     (3)                                                                                                          

где  представляет собой длительность внешнего ударного воздействия. В дальнейшем будем полагать, что

                                                                 .                         (4)

При разработке и эксплуатации устройств, реализующих принцип МСК, необходимо точное знание величины , т.к. в противном случае аппаратура посчитает в качестве одного из участков , что приведет к резкому возрастанию погрешности измерения. Первой и основной частью решаемой задачи будет являться выбор оптимальной формы и длительности внешнего (ударного) воздействия, т.к. выбор этих параметров влияет на получаемую в ОК амплитуду собственных колебаний и, следовательно, позволяет применять в приборах измерительные элементы необходимой чувствительности и разрешающей способности (если разговор идет о программной реализации детектирования, то это число уровней квантования АЦП). Большое внимание вопросам аппроксимации ударного воздействия уделено в /15, 16/.

Большинство практических задач решаются путем аппроксимации ударных воздействий классическими функциями. Рассмотрим наиболее употребительные классические сигналы, применяемые для аппроксимации ударных воздействий.