Министерство образования Российской Федерации
Красноярский Государственный Технический Университет
Институт радиоэлектроники
Кафедра: КиПР
Отчет по лабораторным работам (№1-6)
Выполнил: ст-т гр Р31-3
Глухих Н.А.
Проверил: Томилин В. И.
КРАСНОЯРСК 2003г.
1 ВВЕДЕНИЕ
В последние годы внимание физиков, химиков и технологов, занимающихся исследованиями полупроводников, привлекает проблема атомной диффузии в полупроводниковых структурах. Этот интерес вызван стремлением выяснить физические закономерности, которые присущи диффузионным процессам, а также потребностями современной технологии создания полупроводниковых приборов.
Диффузией называется процесс выравнивания плотностей, обусловленный переносом вещества посредством молекулярного движения. Переносимая через поверхность площадью S за время t масса вещества
|
![]()
где ![]() -
разность плотностей между двумя точками, расстояние между которыми по направлению
наибольшего изменения плотности равно
-
разность плотностей между двумя точками, расстояние между которыми по направлению
наибольшего изменения плотности равно ![]() :
: ![]() называется градиентом плотности; D-коэффициент диффузии.
называется градиентом плотности; D-коэффициент диффузии.
Коэффициентом
диффузии называется величина, равная массе диффундирующего вещества через
единичную поверхность ха единицу времени при градиенте плотности, равном
единице. Единица коэффициента диффузии – квадратный метр в секунду ![]() . 1
. 1 ![]() равен
коэффициенту диффузии такой среды, в которой при градиенте плотности 1
равен
коэффициенту диффузии такой среды, в которой при градиенте плотности 1 ![]() за 1
за 1 ![]() через
площадь 1
через
площадь 1 ![]() переносится масса вещества в 1
переносится масса вещества в 1 ![]() (поверхность располагается
перпендикулярно к направлению переноса массы).
(поверхность располагается
перпендикулярно к направлению переноса массы).
Диффузионное движение носителей зарядов обусловливает прохождение диффузионного тока электронов и дырок, плотности которых определяются из соотношений:
|
|
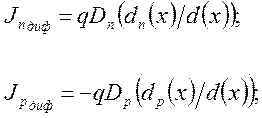
где ![]() ,
,
![]() - градиенты концентрации электронов
т дырок; Dn и Dp
- коэффициенты диффузии электронов и дырок. Знак минус означает противоположную
направленность электрических токов в полупроводнике при диффузионном движении
электронов и дырок в сторону уменьшения их концентраций.
- градиенты концентрации электронов
т дырок; Dn и Dp
- коэффициенты диффузии электронов и дырок. Знак минус означает противоположную
направленность электрических токов в полупроводнике при диффузионном движении
электронов и дырок в сторону уменьшения их концентраций.
Градиент концентрации характеризует степень неравномерности распределения зарядов (электронов и дырок) в полупроводнике вдоль какого-то выбранного направления.
Коэффициенты диффузии связаны с подвижностями носителей зарядов соотношениями Эйнштейна:
|
![]()
|
![]()
Для осуществления диффузии при отсутствии внешних сил необходима флуктуация тепловой энергии. А так как её распределение в твердом теле подчиняется статистике Максвелла-Больцмана, то вероятность таких флуктуаций и, следовательно, вероятности диффузионных перескоков атомов f пропорциональна величине
|
![]() .
.
Уравнение ![]() , называемое первым законом Фика,
справедливо для стационарной диффузии, когда в любой точке сечения,
перпендикулярного потоку, градиент концентрации остается постоянным во времени.
, называемое первым законом Фика,
справедливо для стационарной диффузии, когда в любой точке сечения,
перпендикулярного потоку, градиент концентрации остается постоянным во времени.
По закону сохранения вещества, разность потоков должна быть равна изменению концентрации внутри рассматриваемого объема:
|
![]() .
.
Учитывая первый закон Фика, получим:
|
![]() .
.
|
![]() ,
,
где Ñ - оператор градиента
Если D не зависит от концентрации, то формула будет иметь вид
|
![]() ,
,
где ![]() -
оператор Лапласа.
-
оператор Лапласа.
Тогда для одномерного случая
|
![]() .
.
В зависимости от начальных и граничных условий это уравнение имеет несколько решений.
Начальные
условия задают распределение примесей в момент времени ![]()
![]() , а граничные распределения примесей
по поверхности или объему в произвольный момент времени
, а граничные распределения примесей
по поверхности или объему в произвольный момент времени ![]() при
при
![]() .
.
По типу начальных условий диффузионные задачи подразделяются:
1. задачи на удаление вещества из твердого тела (обезгаживание, геттерирование примесей и т.д.);
2. задачи на введение вещества в объем твердого тела (легирование полупроводников, поглощение газов и т.д.)
Диффузионные понятия
1) неограниченное тело – тело, размеры которого много больше диффузионной длины;
2) полуограниченное
тело – которое с одной стороны ограниченно плоскостью ![]() ,
а с другой стороны простирается на расстояние, много большее диффузионной
длины;
,
а с другой стороны простирается на расстояние, много большее диффузионной
длины;
3) тело конечных размеров – тело, размеры которого соизмеримы с диффузионной длиной;
4) неограниченный источник – диффузия осуществляется из источника, в котором концентрация примесей постоянна и не зависит от времени;
5) ограниченный источник – концентрация примесей не восполняется в процессе диффузии;
6) отражающая граница – плоскость, непроницаемая для диффундирующей примеси.
Методы расчета диффузионных структур
При проведении расчетов обычно решаются задачи двух типов:
1) на основании заданного технологического режима определяется профиль распределения концентрации примесей и/или глубину залегания p-n перехода;
2) на основании заданных параметров конечной структуры рассчитываются режимы диффузионного процесса.
1.1РЕШЕНИЕ ДИФФУЗИОННЫХ УРАВНЕНИЙ
1. Расчет распределения примеси в случае двустадийной диффузии:
|
![]()
где N – поверхностная плотность атомов, D1 – коэффициент диффузии, t1 – время загонки
|
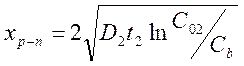
где xp-n – глубина залегания p-n перехода; Cb – исходная концентрация примеси;
![]() ;
D2t2 –
поверхность концентрации примеси к моменту окончания процесса разгонки.
;
D2t2 –
поверхность концентрации примеси к моменту окончания процесса разгонки.
2. Расчет распределения примеси при диффузии из слоя конечной толщины:
|
![]()
![]() -
поверхностная концентрация после разгонки
-
поверхностная концентрация после разгонки
1.2ДИФФУЗИЯ ИЗ БЕСКОНЕЧНО ТОНКОГО ОГРАНИЧЕННОГО ИСТОЧНИКА В НЕОГРАНИЧЕННОЕ ТЕЛО
Данный случай
соответствует условиям, когда в тонком поверхностном слое полупроводника
создается избыточная концентрация примесей![]() ,
и структура подвергается дальнейшей высокотемпературной обработке, во время
которой происходит перераспределение примесей по объему. В ходе этого процесса
количество атомов примеси на поверхности непрерывно уменьшается, а в объеме
возрастает. Для этого случая граничные и начальные условия можно представить в
виде:
,
и структура подвергается дальнейшей высокотемпературной обработке, во время
которой происходит перераспределение примесей по объему. В ходе этого процесса
количество атомов примеси на поверхности непрерывно уменьшается, а в объеме
возрастает. Для этого случая граничные и начальные условия можно представить в
виде:

Начальные условия: ![]() ;
;
![]()
Граничные условия: ![]()
Решение 2-го уравнения Фика при данных условиях имеет вид:
|
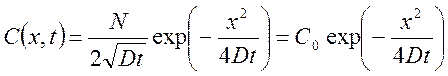
где 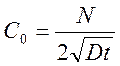 -
поверхностная концентрация
-
поверхностная концентрация
Поскольку функция четная, то кривые, описывающие распределение концентрации вдоль оси Х, симметричны относительно точки х=0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.