






















Министерство образования Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
«Алтайский государственный технический университет
им. И.И. Ползунова»
О.Р. Светлова, Э.А. Алексеева, Г.Д. Леонова
СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА
Способ замены плоскостей проекций
Способы вращения
Методические рекомендации по курсу начертательной геометрии для самостоятельной работы студентов специальностей 230100,171500,340100,130400,120100 дневной, вечерней и заочной форм обучения
Бийск 2003
УДК 515,(075.8)
Светлова О.Р., Алексеева Э.А., Леонова Г.Д. Способы преобразования чертежа: Способ замены плоскостей проекций. Способы вращения:
Методические рекомендации по курсу начертательной геометрии для самостоятельной работы студентов специальностей 230100, 171500, 340100, 130400, 120100 дневной, вечерней и заочной форм обучения.
Алт. гос. техн. ун-т , БТИ.- Бийск:
Изд-во Алт. гос. техн. ун-та, 2003. – 25 с.
В методических рекомендациях представлен теоретический материал и примеры решения задач по темам: способы преобразования проекции; способ замены плоскостей проекций; способы вращения. Методические рекомендации по курсу начертательной геометрии предназначены для самостоятельной работы студентов специальностей 230100, 171500, 340100, 130400, 120100 дневной, вечерней и заочной форм обучения.
Рассмотрены и одобрены
на заседании кафедры
технической графики.
Протокол № 17 от 16 октября 2003 г.
Рецензент: к.т.н. Светлов С.А. проф. Кафедры ТХМ
ВВЕДЕНИЕ
Количество графических построений, необходимых для решения той или иной задачи, часто зависит не столько от сложности этой задачи, сколько от расположения проектируемой пространственной формы по отношению к плоскостям проекций.
Вспомним решение двух примеров.
Пример 1. Определить истинную величину отрезков АВ (рисунок 1) и ВС (рисунок 2).
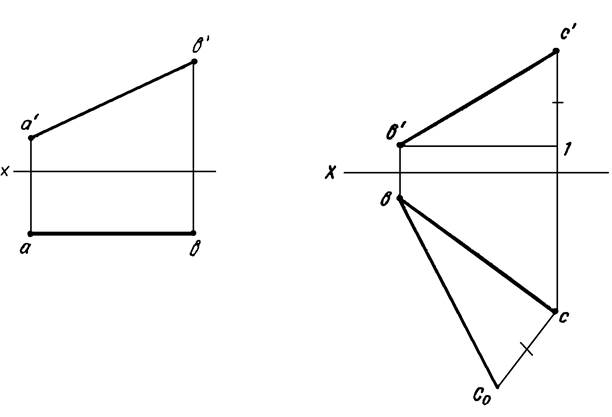
Рисунок 1 Рисунок 2
Отрезок АВ занимает частное положение относительно заданной системы плоскостей проекций — он параллелен плоскости проекций V. В этом случае фронтальная проекция отрезка АВ определяет истинную величину его (a’b’ = АВ). Отрезок ВС занимает общее положение относительно заданной системы плоскостей проекций и, следовательно, ни одна из его проекций не определяет истинной величины самого отрезка. Истинная величина отрезка ВС определена как гипотенуза bС0 прямоугольного треугольника.
Пример 2. Определить расстояние от точки А до плоскости Р (рисунок 3) и от точки В до плоскости Q (рисунок 4).
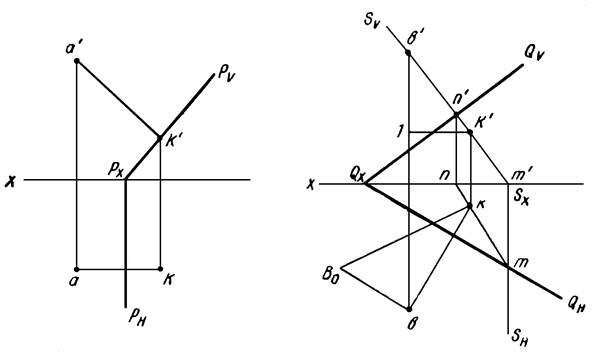
Рисунок 3 Рисунок 4
Плоскость P — плоскость частного положения (фронтально проектирующая). Расстояние от точки А до плоскости P определяется перпендикуляром a’k’, опущенным из фронтальной проекции (a’) точки А на фронтальный след (PV ) плоскости Р.
Плоскость Q — плоскость общего положения. Как видно из рисунка 4 для определения расстояния от точки В до плоскости Q выполнен целый ряд вспомогательных построений — опущен перпендикуляр из точки В на плоскость Q, найдено его основание (точка K), определена истинная величина перпендикуляра.
Из рассмотренных примеров следует, что решение ряда задач значительно упрощается, если заданные геометрические элементы находятся в частных положениях относительно плоскостей проекций.
В начертательной геометрии можно путем несложных построений перейти от общих положений заданных геометрических элементов к частным. Эти построения сводятся к замене плоскостей проекций и вращению вокруг осей.
СПОСОБ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Этот способ заключается в том, что одна из плоскостей проекций заменяется новой плоскостью, перпендикулярной к остающейся (незаменяемой) плоскости проекций. Положение в пространстве изображенного тела при этом остается неизменным.
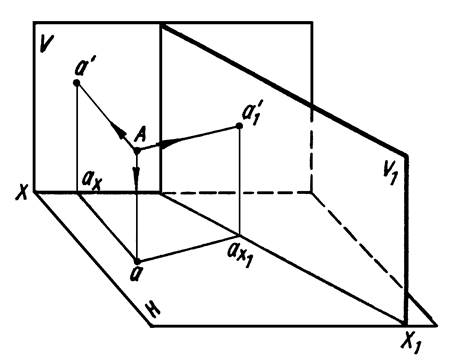
Рисунок 5
На рисунке 5 изображена точка A в системе V/H. Затем плоскость V заменена плоскостью проекций V1, которая также перпендикулярна к Н. Образовалась система V1/H. Плоскость V1 пересеклась с плоскостью Н по прямой Х1, которая и будет являться новой осью проекций в новой системе.
Горизонтальная проекция точки А своего положения не меняет. Для нахождения фронтальной проекции (a’1) точки A в системе V1/H опущен перпендикуляр из точки А на плоскость проекций V1. Из чертежа видно, что aA = аx1а'1. Но аA= аxа', следовательно, аx1а'1= аxа', т. е. расстояние от новой фронтальной проекции а' точки А до новой оси проекций Х1 равно расстоянию от старой фронтальной проекции а' этой точки до старой оси проекций X.
Для перехода от пространственного изображения к чертежу надо плоскость v1 вращением около новой оси проекции X1 совместить с плоскостью Н.
Построение проекции а'1 на эпюре (рисунок 6) производится в следующем порядке:
а) из горизонтальной проекции а точки А опускается перпендикуляр на новую ось проекций Х1;
б) на этом перпендикуляре от точки ах1 откладывается отрезок аx1а'1, равный расстоянию от старой фронтальной проекции а' до старой оси проекций X.
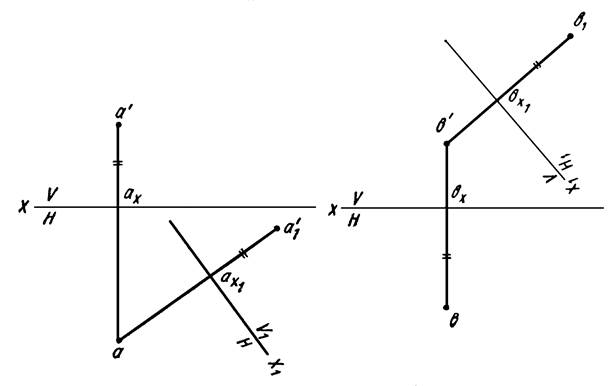
Рисунок 6 Рисунок 7
На рисунке 7 произведена замена горизонтальной плоскости проекций Н новой плоскостью Н1, перпендикулярной V, т. е. осуществлен переход от системы V/H к системе V/H1. Все построения аналогичны рассмотренным выше и понятны из чертежа.
Рассмотрим несколько примеров.
Пример 3. Определить истинную величину отрезка АВ (рисунок 8).
В заданной системе плоскостей проекции V/H отрезок занимает общее положение.
Заменим плоскость проекций V новой плоскостью V1, параллельной заданному отрезку АВ. Новая ось проекций Х1 при этом, очевидно, должна быть параллельна горизонтальной проекции ab отрезка. Для нахождения новой фронтальной проекции отрезка построены новые фронтальные проекции его концов (точек А и В) в системе V1/H. Новая фронтальная проекция а'1b'1 отрезка — истинная величина отрезка АВ.
На рисунке 9 эта же задача решена путем замены плоскости проекций H новой плоскостью H1. В этом случае новая ось должна быть расположена параллельно а'b'. Новая горизонтальная проекция (а1b1) отрезка — его истинная величина.
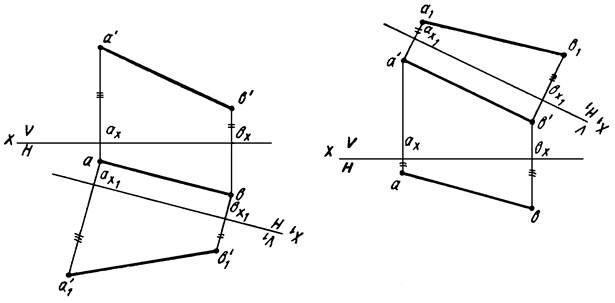
Рисунок 8 Рисунок 9
Пример 4. Определить расстояние от точки S до плоскости треугольника ABC (рисунок 10).
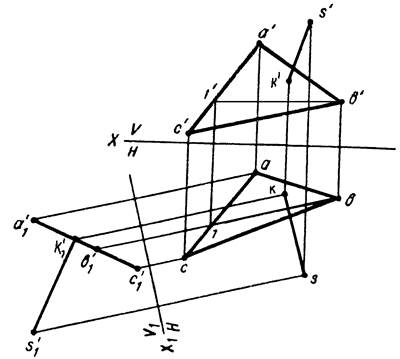
Рисунок 10
Расстояние от точки до плоскости может быть определено непосредственно на эпюре, если плоскость будет проектирующей.
Заменим плоскость V на новую плоскость проекций v1. Плоскость v1 выберем так, чтобы она оказалась перпендикулярной плоскости треугольника АВС. Новая ось проекции Х1 при этом должна быть перпендикулярна горизонтальной проекции горизонтали.
Пример 5. Определить угол наклона плоскости Р к горизонтальной плоскости проекций (рисунок 11).
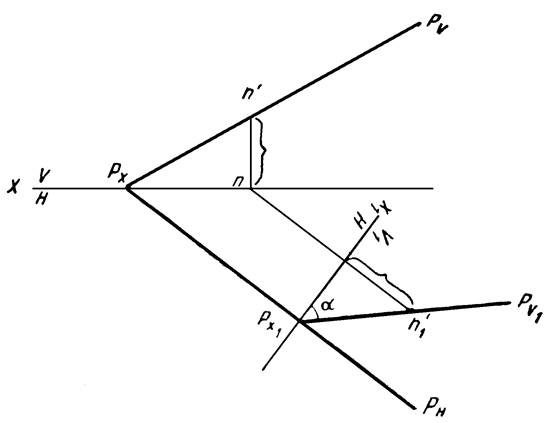
Рисунок 11
Если плоскость, заданная следами, фронтально проектирующая, то угол, образованный фронтальным следом с осью проекций, и будет определять угол наклона плоскости к горизонтальной плоскости проекций.
Заменим систему плоскостей V/H новой системой V1/H. Новую ось X1 проведем перпендикулярно РH. Положение следа РH не изменяется. Точка РX1— точка схода следов в новой системе. Для того чтобы найти направление нового фронтального следа (РV1) плоскости, берем на следе РV произвольную точку (N) и находим ее новую фронтальную проекцию (n'1). Через точки РX1 и n'1 проводим новый фронтальный след (РV1) плоскости. Найденный угол α и будет искомым.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.