Государственное образовательное учреждение
высшего профессионального образования
«Алтайский государственный технический университет
имени И. И. Ползунова»
Г. Д. Леонова, Н. Ю. Афанасьева
Взаимное пересечение кривых поверхностей.
Пересечение кривой поверхности с поверхностью многогранника.
Взаимное пересечение многогранников
Курс лекций по начертательной геометрии
для студентов специальностей
230100, 171500, 340100, 130400, 120100
дневной, вечерней и заочной форм обучения
УДК 515,(075.8)
Леонова Г. Д., Афанасьева Н. Ю. Взаимное пересечение поверхностей: Взаимное пересечение кривых поверхностей. Пересечение кривой поверхности с поверхностью многогранника. Взаимное пересечение многогранников:
Курс лекций по начертательной геометрии для студентов специальностей 230100, 171500, 340100, 130400, 120100 дневной, вечерней и заочной форм обучения.
Алт. гос. техн. ун-т, БТИ. – Бийск:
Изд-во Алт. гос. техн. ун-та, 2003. –
Курс лекций предназначен для самостоятельного изучения начертательной геометрии студентами механических специальностей дневной, вечерней и заочной форм обучения.
Рассмотрены и одобрены на заседании кафедры “Технической графики“. Протокол № 15 от 25 марта 2003 г.
Рецензент: к. т. н. Третьяков А. М., БТИ
1 ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ
Кривые поверхности пересекаются в общем случае по пространственной кривой линии, проекции которой строятся обычно по точкам. Точки, принадлежащие линии пересечения, находятся при помощи вспомогательных секущих поверхностей. В качестве вспомогательных секущих поверхностей-посредников применяются плоскости (рисунок 1) или кривые поверхности (например, шаровые). Вспомогательные поверхности выбираются с таким расчетом, чтобы в пересечении их с каждой из заданных поверхностей получились простые и удобные для вычерчивания линии — прямые либо окружности.
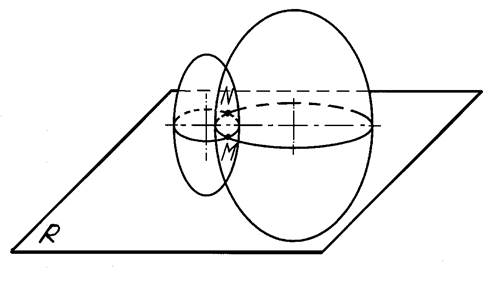
Рисунок 1
В зависимости от вида посредника различают следующие способы построения линии пересечения поверхностей:
а) способ вспомогательных секущих плоскостей:
1) частного положения,
2) общего положения;
б) способ вспомогательных секущих сфер:
1) концентрических,
2) эксцентрических;
в) способ конических и цилиндрических поверхностей.
Линия пересечения поверхностей не должна выходить за пределы площади наложения (общей части проекции двух поверхностей).
Построение начинают с нахождения особых точек: точек, лежащих на очерке, делящих проекции кривых на видимую и невидимую части, а также экстремальных точек – точек крайнего положения кривой пересечения.
Рассмотрим построение проекций линии пересечения двух кривых поверхностей на конкретных примерах.
1.1 Способ вспомогательных секущих плоскостей частного положения
Пример 1. Построить линию пересечения конуса и цилиндра вращения (рисунок 2).
В первую очередь найдены характерные точки линии пересечения: высшая и низшая точки А и Е и точки С и С1, разделяющие горизонтальную проекцию кривой на видимую и невидимую части.
Точки А и Е определены при помощи вспомогательной фронтальной плоскости Q, которая пересекает поверхность цилиндра и конуса по крайним образующим. Пересечения фронтальных проекций этих образующих дают фронтальные проекции а’ и е’ точек А и Е. Горизонтальные проекции точек находятся на горизонтальном следе вспомогательной плоскости QH .
Точки С и С1 найдены при помощи горизонтальной плоскости S, проведенной через ось цилиндра. Плоскость S пересекает поверхность цилиндра по крайним образующим (передней и задней), а поверхность конуса — по окружности. Пересечения горизонтальных проекций крайних образующих и окружности дают точки с и с1 — горизонтальные проекции точек С и С1. Фронтальные проекции этих точек лежат на фронтальном следе плоскости SV.
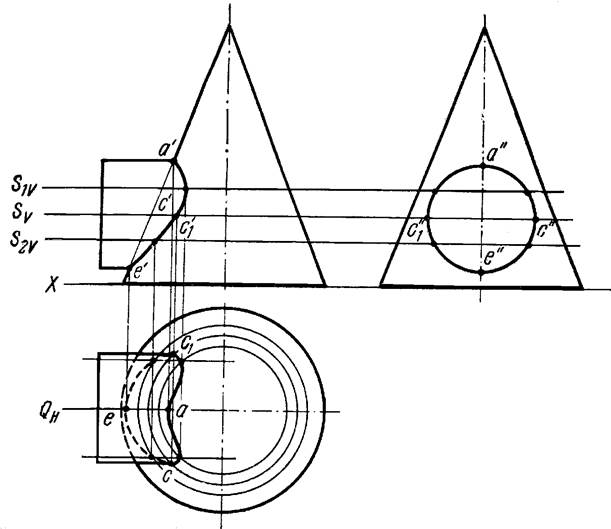
Рисунок 2
Промежуточные точки линии пересечения найдены при помощи горизонтальных плоскостей S1 и S 2.
В рассмотренном примере точки линии пересечения найдены при помощи вспомогательных плоскостей частного положения. Иногда же введение плоскостей частного положения не дает желаемого эффекта и целесообразнее воспользоваться плоскостями общего положения.
1.2 Способ вспомогательных секущих плоскостей общего положения
Пример 2. Построить линию пересечения двух наклонных цилиндров (рисунок 3).
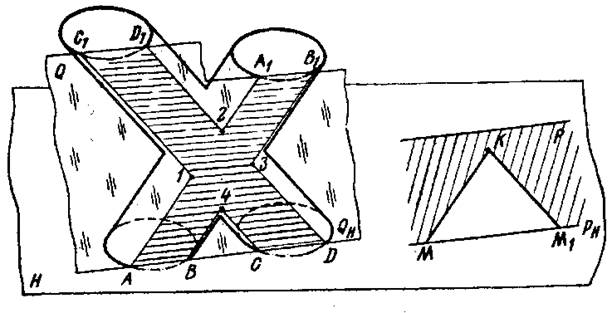
Рисунок 3
В этом случае применение плоскостей частного положения усложнит решение задачи, так как в сечении цилиндров получатся локальные кривые, точное построение которых затруднительно. Наиболее простые линии сечения (прямые) получатся при пересечении заданных наклонных цилиндров плоскостями, параллельными образующим обоих цилиндров, т е. плоскостями общего положения. Для построения таких плоскостей в пространстве взята произвольная точка К, и через нее проведены прямые КМ и КМ1, параллельные образующим цилиндров. Эти пересекающиеся прямые определяют собой некоторую плоскость Р, являющуюся плоскостью параллелизма для заданных цилиндров. Вспомогательная плоскость Q, проведенная параллельно построенной плоскости Р, пересекла поверхность одного цилиндра по образующим АА1 и ВВ1 а второго — по образующим СС1 и DD1. Пересечения этих образующих дают точки 1, 2, 3, 4, принадлежащие линии пересечения цилиндров.
Подробное построение проекций линий пересечения двух наклонных цилиндров на эпюре показано на рисунке 4.
Через произвольно взятую точку К проведена плоскость параллелизма P(горизонтальный след – PH), заданная двумя пересекающимися прямыми, параллельными образующим цилиндров. Затем проводится ряд секущих плоскостей общего положения Q1, Q2,…Q6, параллельных плоскости P. Такие плоскости пересекают оба цилиндра по образующим.
След первой плоскости QH1 проводится параллельно следу PH по касательной к основанию одного из цилиндров (правого). Эта плоскость пересекает поверхность одного цилиндра по образующим, выходящим из точек основания A и B, а второго - по образующей, выходящей из точки C – точки касания плоскости Q .
Пересечения этих образующих дают точки 1,10, принадлежащие линии пересечения цилиндров. Далее следы плоскостей проводятся так, чтобы определились опорные точки линии пересечения, расположенные на очерковых образующих:
cлед QH2 проводится через характерную точку E, из которой выходит очерковая образующая правого цилиндра;
QH3 проводится через точку H, определяющую фронтальную очерковую левого цилиндра;
QH4 – проводится через точку R;
QH5 - проводится через точку I;
QH6 – проводится через точку T – крайняя плоскость, касательная к левому цилиндру.
По расположению следов можно сделать вывод о характере кривой. Так как зоны непересекаемости расположены на разных основаниях, линия пересечения – одна кривая (врезка).
Для соединения полученных точек пересечения используем метод “обхода оснований” цилиндров.
Движемся против часовой стрелки, начиная с точки C, по правому основанию и в том же направлении – по левому – из точки A. На пересечении образующих, выходящих из точек Aи Cполучаем точку 1, из точек Eи G – получаем точку 2, и т. д. Соединяем их последовательно до точки 5, получающейся при пересечении образующих выходящих из точек Tи V. Продолжаем двигаться в том же направлении, (то есть против часовой стрелки) по основанию левого цилиндра, к точкам S, H, D, B, а на другом цилиндре, дойдя до зоны непересекаемости, меняем направление на обратное (по часовой стрелке): от точки Vк точке I,L и т. д. до точки C. Далее продолжаем движение в том же направлении от точки Cк точке W, а на другом основании меняем направление, двигаясь от точкиBк T, и заканчиваем
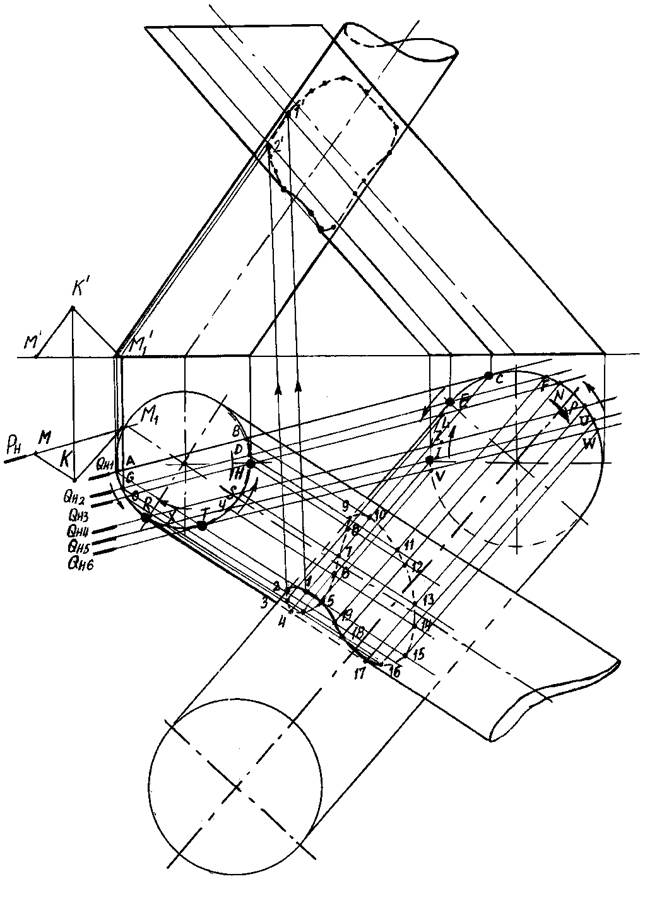
Рисунок 4
обход в том же направлении: от точки T к точке A, а на основании правого цилиндра – возвращаемся от точки W к точке С. Таким образом, соединяем последовательно точки линии пересечения с 1 до 19 на горизонтальной проекции.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.