Для решения этой задачи вспомогательные секущие плоскости выбраны по рассмотренной схеме: через произвольную точку К проведены две пересекающиеся прямые, параллельные соответственно образующим цилиндра и ребрам призмы. Эти пересекающиеся прямые определили собой некоторую плоскость Q, являющуюся плоскостью параллелизма для данных тел. Далее через рёбра призмы (АА1, ВВ1, СС1) проведены плоскости (Р1, Р2, Р3), параллельные плоскости Q. Эти плоскости пересекли поверхность цилиндра по образующим, в пересечении горизонтальных проекций которых с горизонтальными проекциями ребер призмы получены горизонтальные проекции точек встречи ребер призмы с поверхностью цилиндра (1,2,3; 11,21,31); промежуточные точки линии пересечения находят, проводя дополнительные плоскости, также параллельные плоскости Q. Они пересекут поверхность цилиндра по некоторым образующим, а поверхность призмы — по прямым, параллельным ребрам. Показана одна из таких плоскостей — плоскость S, при помощи которой получены промежуточные точки 4 и 41.
3 ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКОВ
Построение линии пересечения двух многогранников сводится к нахождению точек встречи ребер первого многогранника с гранями второго и ребер второго с гранями первого. Затем найденные точки последовательно соединяются прямыми линиями. При этом следует иметь в виду, что соединять между собой можно только те точки, которые лежат на одной и той же грани.
При определении видимости точек, принадлежащих линии пересечения, руководствуются следующим правилом: проекция точки, полученная при пересечении двух видимых линий, видима. Точка пересечения двух невидимых или одной видимой и другой невидимой линии невидима.
Пример З. Построить линии пересечения поверхностей призмы и пирамиды (рисунок 21).
Как видно из чертежа, с поверхностью пирамиды пересекается только одно переднее ребро призмы. Так как это ребро перпендикулярно плоскости Н, то горизонтальные проекции точек входа и выхода (точки 1 и 2) отмечаются непосредственно на эпюре. Для нахождения их фронтальных проекций через вершину пирамиды и переднее ребро призмы проведена вспомогательная горизонтально проектирующая плоскость Q. Она пересекла поверхность пирамиды по прямым SD и SE, в пересечении фронтальных проекций которых с фронтальной проекцией переднего ребра призмы отмечены фронтальные проекции 1’, 2’ точек входа и выхода 1 и 2. Так как грани призмы — горизонтально проектирующие плоскости, то построение точек встречи ребер пирамиды с гранями призмы (точек 3, 4, 5, 6) никаких затруднений не представляет и понятно из чертежа. Соединив последовательно между собой фронтальные проекции найденных точек, получим фронтальную проекцию линии пересечения. Горизонтальная проекция ее совпадает с горизонтальной проекцией призмы.
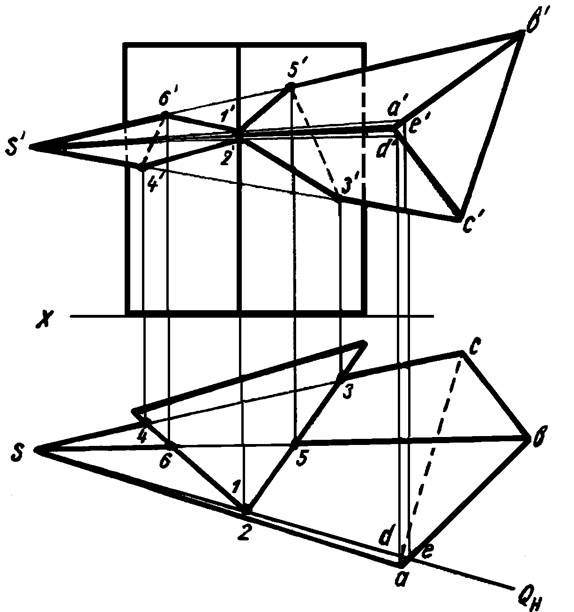
Рисунок 21
|
|
|
Пример 4. Построить линию пересечения поверхностей призмы и пирамиды, основания которых расположены на горизонтальной плоскости проекций (рисунок 22).
Для нахождения точек пересечения ребер одного многогранника с гранями другого вспомогательные секущие плоскости проведены по рассмотренной схеме, т. е. через вершину пирамиды (S) проведена прямая (SM), параллельная ребрам призмы. Затем найден горизонтальный след этой прямой — точка М. В соответствии со схемой горизонтальный след каждой из вспомогательных секущих плоскостей должен пройти через точку М и след заключаемого в плоскость ребра. Проведены три вспомогательные плоскости: Р, Q, и S, при помощи которых найдены горизонтальные проекции точек 1, 2, 3, 4, 5, 6. Фронтальные проекции их отмечены на фронтальных проекциях соответствующих ребер.
Во избежание ошибок в последовательности соединения найденных точек при выполнении построений следует записывать, какому ребру одного многогранника, и какой грани второго принадлежит данная точка. Эту запись удобно вести в графической форме. Строится схема наложенных одна на другую разверток боковых поверхностей пересекающихся тел (рисунок 23).
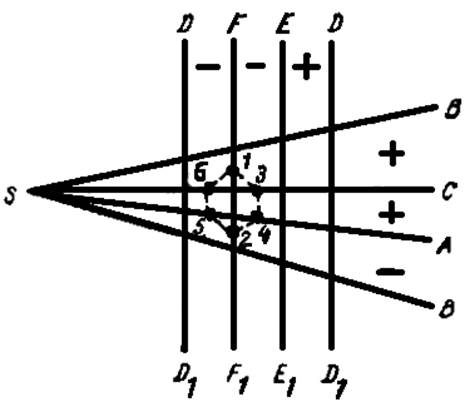
Рисунок 23
Найденные на эпюре точки наносят на схему так, чтобы их наложение соответствовало действительному положению точек на ребрах одного многогранника и гранях другого. Затем нанесенные на схему точки последовательно соединяют прямыми линиями, определяя тем самым порядок соединений их проекций на эпюре. В нашем примере этот порядок следующий (рисунок 23): 1−3−4−2−5−6−1.
Приведенной схемой удобно пользоваться и для определения видимости отдельных звеньев линии пересечения. Для этого условно знаком «+» обозначают видимые грани, а знаком «—» невидимые. Эти обозначения необходимо выполнить отдельно на горизонтальной и фронтальной проекциях. Затем вступает в силу изложенное правило для определения видимости точек. На схеме (рисунок 23) видимость определена для горизонтальной плоскости проекций.
1. Гордон В. О., Семенцов–Огиевский М. А. Курс начертательной геометрии: Учебное пособие/ Под ред. Ю. Б. Иванова. – 23-е изд., перераб. – М: Наука. Гл. ред. физ.-мат. лит., 1988. – 272 с.
2. Начертательная геометрия/ Под общей ред. Ю. Г. Козловского. – Минск: Изд-во «Вышейшая школа», 1967.
3. Чекмарев А. А. Инженерная графика: Учеб. для немаш. спец. вузов. – 2-е изд., испр. – М.: Высш. шк., 1998.
1. Взаимное пересечение кривых поверхностей
2. Пересечение кривой поверхности с поверхностью многогранника
3. Взаимное пересечение многогранников
Литература
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.