Пример 6. Этот способ применяют тогда, когда нельзя применить способ концентрических сфер, так как оси поверхностей вращения не пересекаются (рисунок 14). Отмечаем точки 1’ и 6’ – пересечение очерковых образующих (так как имеется общая фронтальная плоскость симметрии).
Проводим секущие плоскости через ось кольца О’, перпендикулярные к фронтальной плоскости V. Плоскость PV1 пересекает тор по окружности, проекцией, которой является прямая А’B’. Подбираем к ней сферу – центр её будет лежать в точке D’, на перпендикуляре C’D’ к следу PV.
Эта сфера пересечет конус по окружности, которая на фронтальной проекции спроецируется в линию E’F’. Пересечение A’B’и F’E’ – точка 2’ – точка линии пересечения. Затем проводится еще ряд плоскостей PV2, PV3. Аналогично получаются точки 3’, 5’. Горизонтальные проекции точек получаем переносом с фронтальной проекции. Точка 4, лежащая на горизонтальном очерке, – граница видимости линии пересечения (на фронтальной проекции отмечается на оси тора).
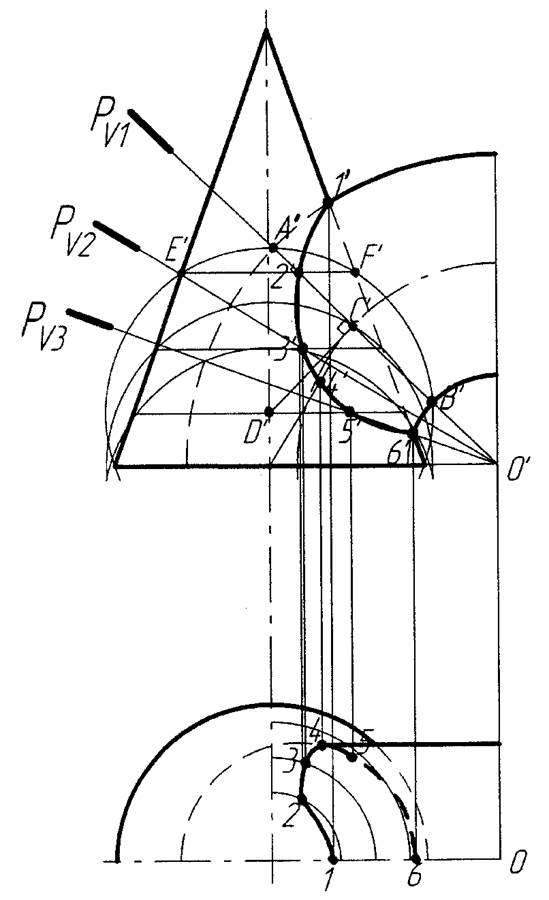
Рисунок 14
Пример 7. Построение двух линий пересечения двух поверхностей имеющих общую плоскость симметрии (параллельную V). Одна из поверхностей – прямой круговой цилиндр, другая – наклонный круговой конус (рисунок 15). Он имеет ряд круговых параллельных между собой сечений, центры которых лежат на одной линии, пересекающей ось поверхности вращения (цилиндра). Определяем опорные точки а и в. Проводим сечение конуса 1-1, параллельное основанию конуса. Из его центра с1, возводим перпендикуляр до пересечения с осью цилиндра – получается точка О1. Из точки О1 описываем сферу 1 радиусом О11, которая пересекает цилиндр по линии 2-2. На пересечении 1-1 и 2-2 получаем точку dлинии пересечения поверхностей и т.д.
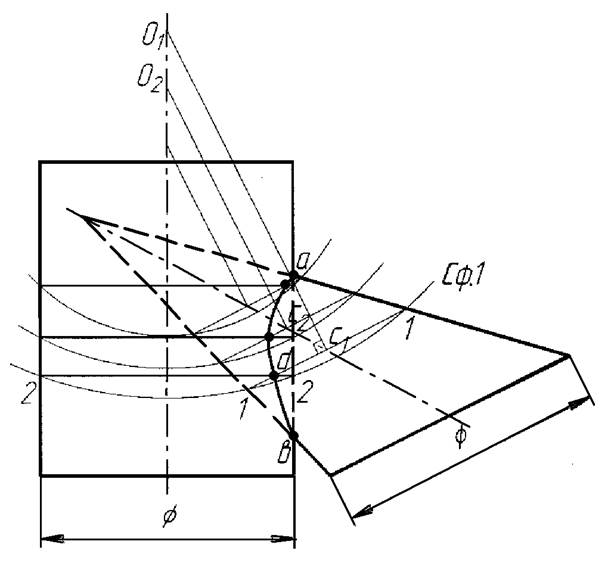
Рисунок 15
1.5 Способ вспомогательных конических и цилиндрических поверхностей
Применяется при построении линии пересечения конических или цилиндрических поверхностей с любой поверхностью вращения при общем расположении этих поверхностей. Способ основан на том, что два цилиндра с параллельными образующими, два конуса с общей вершиной пересекаются по общим образующим (рисунок 16).
Рисунок 16
Пример 8. Пересечение сферы и конической поверхности (рисунок 17).
Основание конуса – эллипс. В качестве посредника используется наклонный круговой конус, ось которого проходит через вершину заданного конуса и центр сферы.
На рисунке 17 показан пример нахождения двух точек А и В линии пересечения с использованием одного вспомогательного секущего конуса, образующие которого на фронтальной проекции проведены через экватор сферы. Для получения всей линии пересечения используются еще несколько секущих поверхностей.
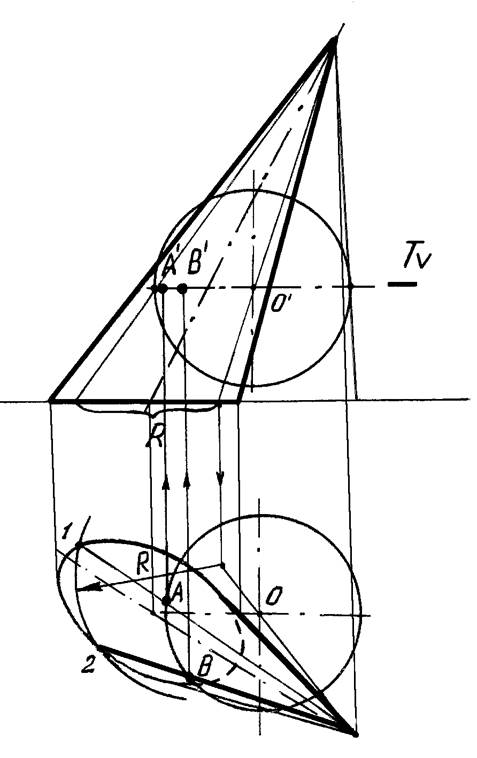
Рисунок 17
Пример 9. Пересечение сферы и наклонного цилиндра, в основании которого – эллипс (рисунок 18).
В качестве посредника используется цилиндрическая поверхность (в основании круг), ось которой проходит через ось сферы параллельно образующей заданного цилиндра. На рисунке 18 показан пример нахождения двух точек линии пересечения А и В, полученных при помощи вспомогательного цилиндра, проходящего через плоское сечение сферы QV – точки 1’ – 2’.
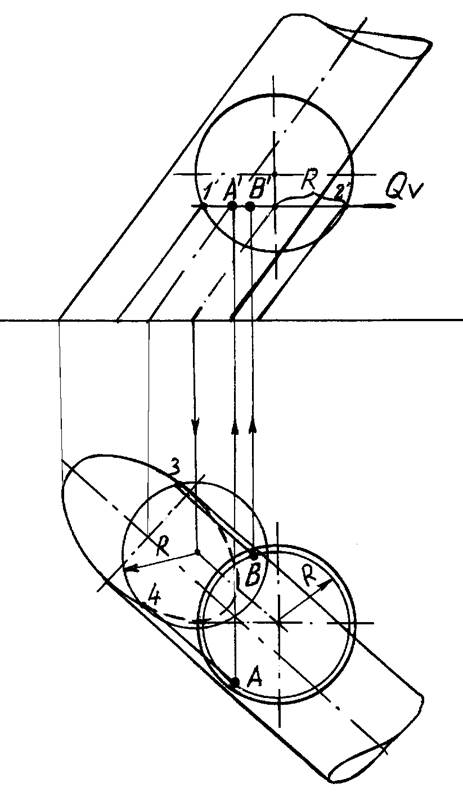
Рисунок 18
Каждая грань многогранника в общем случае пересекает кривую поверхность по плоской кривой. Эти кривые пересекаются между собой в точках встречи ребер многогранника с поверхностью. Таким образом, задача на построение линии пересечения кривой поверхности с многогранником сводится к нахождению линии пересечения поверхности плоскостью и точек встречи прямой с поверхностью.
Рассмотрим примеры.
Пример 1. Построить линию пересечения поверхностей полусферы и призмы (рисунок 19).
Каждая грань призмы пересекает поверхность полусферы по полуокружностям, которые пересекаются между собой в точках встречи ребер призмы с поверхностью полусферы. В приведенном примере одна из граней призмы расположена параллельно фронтальной плоскости проекций, поэтому окружность, по которой эта грань пересекает поверхность полусферы, спроектируется на фронтальную плоскость проекций без искажения. Фронтальные проекции остальных двух дуг полуокружностей, очевидно, будут представлять собой дуги полуэллипсов. Построение их на эпюре следует начинать с нахождения опорных точек. Для этого через каждое ребро призмы проведены фронтальные плоскости (P и Q), которые пересекают поверхность полусферы по окружностям. Точки пересечения фронтальных проекций ребер с соответствующими полуокружностями являются фронтальными проекциями точек встречи ребер призмы с полусферой (точек 1, 2, 3).
Точки 4 и 5, разделяющие кривые на видимую и невидимую части, получены при помощи фронтальной плоскости (S), проведенной через центр полусферы.
Промежуточные точки найдены аналогичным построением (при помощи фронтальных плоскостей Т и Т1).
Рассмотрим теперь более общий случай пересечения поверхностей, когда в качестве вспомогательных секущих плоскостей целесообразно применять плоскости общего положения.
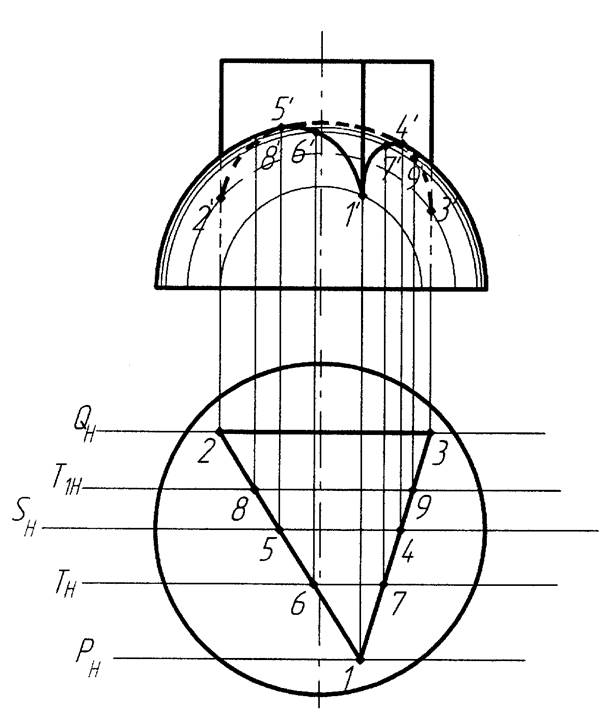
Рисунок 19
Пример 2. Построить линию пересечения поверхности наклонного эллиптического цилиндра с поверхностью трехгранной призмы (рисунок 20).
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.