Определяем видимость: видимые точки линии пересечения получаются при пересечении двух видимых образующих. Видимая часть линии – в интервале между точками 2 – 1 – 19 – 18 – 17 (точки 2 и 17 лежат на очерковых образующих).
Фронтальная проекция линии пересечения строится путём переноса точек с горизонтальной проекции. На рисунке 4 показан пример получения точек 1' и 2'. Строятся фронтальные проекции образующих, при пересечении которых получаются точки линии пересечения. Соединяются между собой в той же последовательности, что и на горизонтальной проекции.
Описанный прием применим также при построении линии пересечения цилиндра и призмы и двух призм.
Пример 3. Построить линию пересечения двух конических поверхностей (рисунок 5).
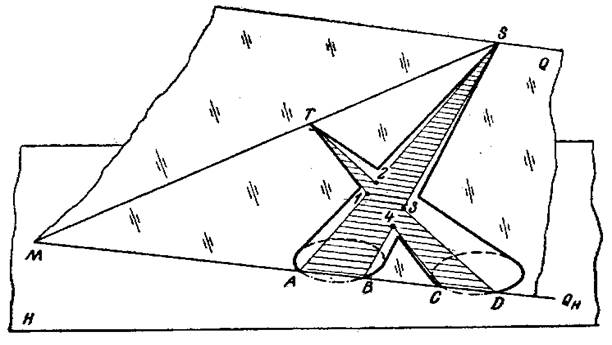
Рисунок 5
Наиболее рациональными в данном случае будут вспомогательные плоскости, проходящие через вершины конусов, так как они будут пересекать заданные поверхности по образующим, т. е. по прямым линиям. Удовлетворять этим требованиям будет любая плоскость, проходящая чёрез прямую ST, проведенную через вершины конусов.
Проведена одна такая плоскость Q. Она пересекла один конус по образующим ASи BS, а второй - по образующим TC и TD. Пересечения этих образующих — точки 1, 2, 3, 4 принадлежат искомой линии пересечения.
Этот прием применим также при построении линии пересечения конуса и пирамиды и двух пирамид.
Пример 4. Построить линию пересечения цилиндрической и конической поверхностей (рисунок 6).
Обе заданные поверхности будут пересекаться по прямым линиям (образующим) плоокостями, проведенными через прямую SM, проходящую через вершину конуса S и параллельную образующим цилиндра. Показана одна такая плоскость — плоскость Q. Поверхность цилиндра она пересекает по образующим АА1 и ВВ1, а конуса — по образующим SCи SD. Точки 1, 2, 3, 4 принадлежат искомой линии пересечения.
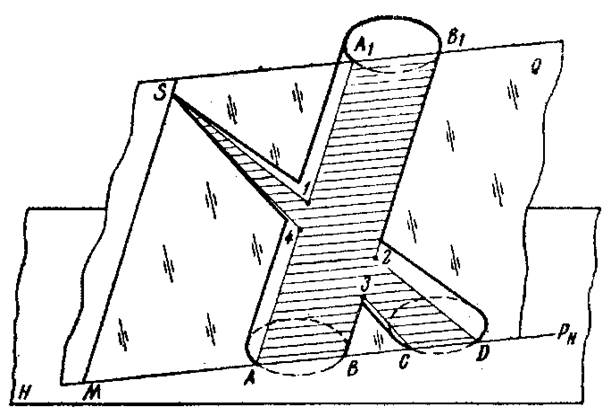
Рисунок 6
Возможные формы кривой линии пересечения в зависимости от расположения следов крайних плоскостей относительно следов поверхности:
1) проницание: линия пересечения распадается на две отдельные пространственные кривые (рисунок 7);
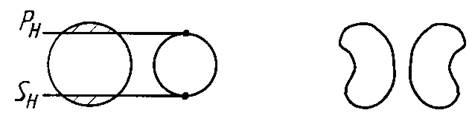
Рисунок 7
2) врезка (врубка): линии пересечения – одна кривая (рисунок 8);
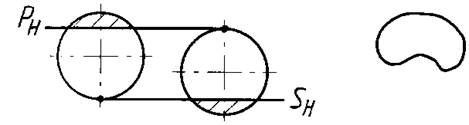
Рисунок 8
3) касание: линия пересечения – две кривые с общей точкой касания (рисунок 9);
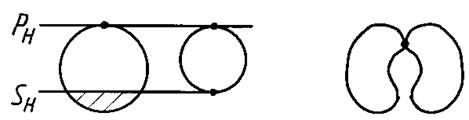
Рисунок 9
4) двойное касание: линия пересечения – две кривые, имеющие две точки касания (рисунок 10).
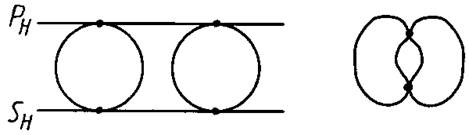
Рисунок 10
Аналогичным приемом строятся линии пересечения призмы и пирамиды, пирамиды и цилиндра, конуса и призмы.
1.3 Способ вспомогательных концентрических сфер
При построении линии пересечения двух поверхностей вращения часто целесообразно применять в качестве вспомогательных секущих поверхностей концентрические сферы (рисунок 11). Это обусловлено тем, что всякая сфера с центром на оси поверхности вращения пересекает любую поверхность вращения по окружности,
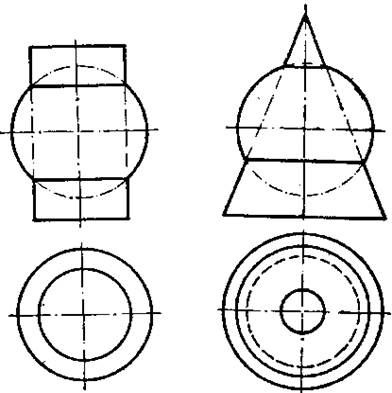
Рисунок 11
т. е. по линии, построение которой не вызывает затруднений. Если при этом оси двух пересекающихся поверхностей вращения пересекаются и параллельны одной из плоскостей проекций, то всякая сфера с центром в точке пересечения осей пересечет каждую из поверхностей по окружностям, которые проектируются на одну из плоскостей проекций в виде отрезков прямых.
Пример 5. Построить линию пересечения конуса вращения и цилиндра вращения (рисунок 12).
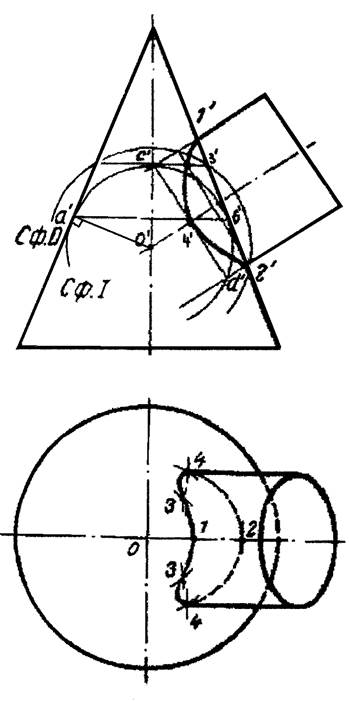
Рисунок 12
Оси заданных поверхностей вращения пересекаются (точка О) и параллельны плоскости проекций V, следовательно, необходимые для применения способа сфер условия имеются. Точки 1’ и 2’ — фронтальные проекции точек пересечения крайних образующих конуса и цилиндра – отмечаются на эпюре непосредственно, без каких бы то ни было построений. Для нахождения промежуточных точек из точки О описана сферическая поверхность Сф.I наименьшего диаметра. Она только касается поверхности конуса и, следовательно, пересекает ее по окружности, фронтальная проекция которой — прямая а’b’. Поверхность цилиндра Сф.I пересекает также по окружности, фронтальная проекция которой — прямая с’d’. Пересечение этих прямых — точка 4’ есть фронтальная проекция одной из точек искомой линии пересечения. Аналогично при помощи Сф.II построена фронтальная проекция З’ еще одной точки, принадлежащей линии пересечения. Горизонтальные проекции найденных точек могут быть построены как проекции точек, лежащих на поверхности конуса.
В начале лекции отмечалось, что линия пересечения двух кривых поверхностей в общем случае представляет собой пространственную кривую. Однако в некоторых частных случаях эта линия может распадаться на плоские кривые. Частные случаи пересечения поверхностей второго порядка определены рядом теорем, излагаемых в соответствующих курсах на геометрии. Приведем две из них без доказательства.
1). Теорема Монжа: две поверхности второго порядка, описанные около третьей поверхности второго порядка (или в нее вписанные), пересекаются между собой по двум кривым второго порядка (рисунок 13).
2). Теорема о двойном соприкосновении: если две поверхности второго порядка имеют две точки соприкосновения, то линии их пересечения распадаются на две кривые второго порядка, проходящие через точки соприкосновения (рисунок 13).
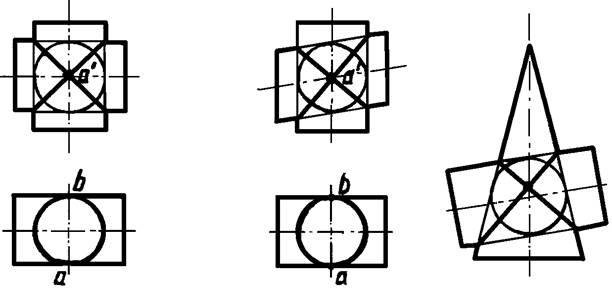
Рисунок 13
1.4 Способ вспомогательных эксцентрических сфер
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.