На рисунке 24 определена истинная величина треугольника ABC способом вращения без указания положения осей. Сначала вращением вокруг некоторой оси, перпендикулярной плоскости Н (положение ее на чертеже не указано), треугольник поставлен перпендикулярно плоскости V, затем поворотом вокруг какой-либо оси, перпендикулярной плоскости V, треугольник приведен в положение, параллельное горизонтальной плоскости проекций H.
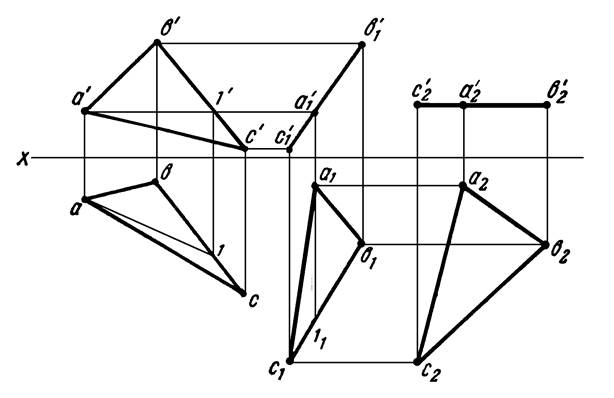
Рисунок 24
Истинную величину плоской фигуры можно определить также путем вращения ее вокруг оси, параллельной плоскости проекций, т. е. вокруг горизонтали или фронтали.
На рисунке 25 определена истинная величина треугольника AВС вращением его вокруг горизонтали AD до положения, параллельного плоскости H. Точки А и D находятся на оси вращения. Они при вращении треугольника своего положения не изменяют. Точки В и C в пространстве перемещаются по окружностям с центрами, расположенными на оси вращения AD. Дуга окружности, которую описывает при вращении точка В, спроектируется на плоскость H в виде прямой, перпендикулярной к ad,. Точка o пересечения этой прямой с ad, будет являться горизонтальной проекцией центра вращения точки В, фронтальная проекция его — точка о’.
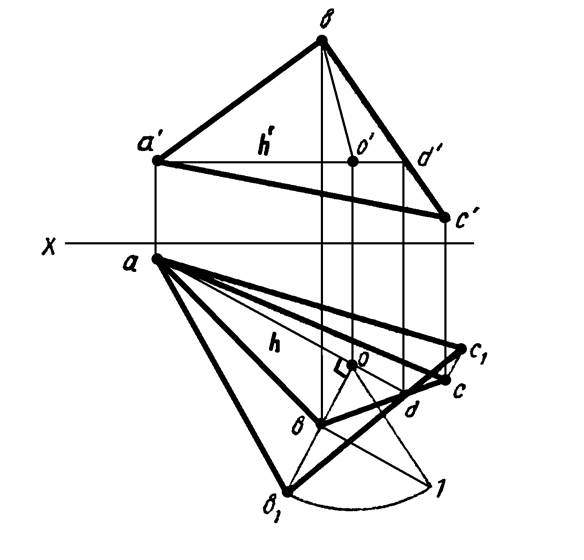
Рисунок 25
Истинная величина радиуса вращения точки В (01) определена способом прямоугольного треугольника. На пересечении дуги этого радиуса, описанной из точки о, с продолжением перпендикуляра ob получена проекция b1 повернутой точки В. Затем точка b1 соединена с точкой d — получено новое направление стороны bc. Положение точки c1 найдено на пересечении перпендикуляра, проведенного из точки с к прямой ad, и прямой b1d определяющей новое направление стороны bc.
Когда плоскость задана следами, то истинную величину фигур, лежащих в этой плоскости, можно определить способом совмещения.
Способ совмещения является частным случаем способа вращения плоскости вокруг горизонтали или фронтали, когда за ось вращения принимается горизонтальный или фронтальный след плоскости.
Сущность способа совмещения состоит в том, что плоскость Р (рисунок 26) вращением вокруг следа PH совмещается с плоскостью проекций H.
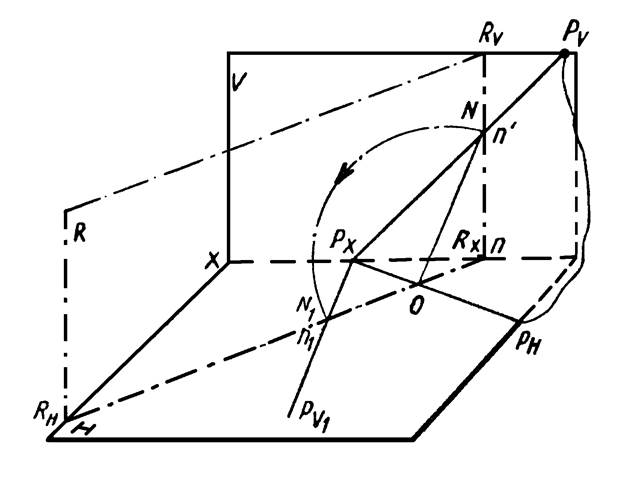
Рисунок 26
Горизонтальный след плоскости (ось вращения) при этом остается на месте. Для нахождения совмещенного положения (PV1 ) фронтального следа плоскости Р определяют совмещенное положение некоторой точки N, произвольно взятой на PV. Эта точка при совмещении плоскости Р с плоскостью проекций Н будет перемещаться в пространстве по дуге окружности радиуса ON, лежащей в плоскости R, перпендикулярной горизонтальному следу PH плоскости Р, т. е. оси вращения. Совмещенное положение N1 точки N определилось в пересечении этой дуги с горизонтальным следом RH плоскости R. Прямая, проходящая через тачки PX и N1, и есть PV1.
На рисунке 27 это же построение выполнено на эпюре. Истинная величина радиуса вращения ON0 точки N определена способом треугольника.
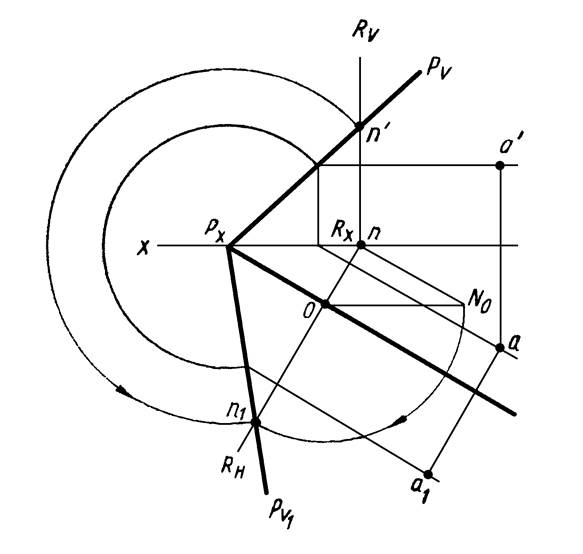
Рисунок 27
Когда точка схода следов PX плоскости находится в пределах чертежа (см. рисунок 27), совмещенное положение точки N можно найти более простым построением. Так как PXn’ = PXn1,то, проведя из точки PX дугу радиуса PXn’ до пересечения со следом RH, найдем совмещенное положение точки N.
Чтобы совместить с плоскостью H точку, принадлежащую плоскости Р, но не лежащую на следе PX, нужно найти совмещенное положение горизонтали, проходящей через заданную точку, и из горизонтальной проекции точки опустить перпендикуляр на след PH до пересечения с совмещенной горизонталью (точка А на рисунке 27).
При помощи способа совмещения можно построить в плоскости общего положения фигуру, форма и размеры которой заданы.
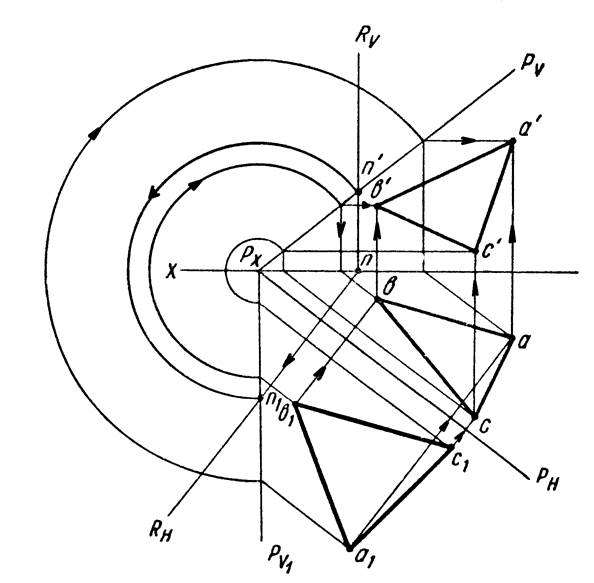
Рисунок 28
В качестве примера на рисунке 28 построены проекции равностороннего треугольника AВС, лежащего на плоскости Р, при заданной горизонтальной проекции его стороны (АВ). Для этого вначале найдена фронтальная проекция стороны АВ. Затем плоскость Р совмещена с горизонтальной плоскостью проекций Н и найдено совмещенное положение a1b1 стороны АВ. Далее, в плоскости Н построен в натуральную величину треугольник a1b1c1 и затем по совмещенному положению c1 точки С построены ее проекции c и c1.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Какие способы преобразования чертежа рассматриваются в методических рекомендациях?
2. В чем заключается основное различие тип способов?
3. В чем заключается способ, известный под названием «способ перемены плоскостей проекций»?
4. Как найти длину отрезка прямой линии и углы эти прямой с плоскостями H и V вводя дополнительные плоскости проекций?
5. Сколько дополнительных плоскостей надо ввести в систему H, V, чтобы определить натуральный вид фигуры, плоскость которой перпендикулярна к пл. H, или к пл. V?
6. В чем заключается способ вращения?
7. Как перемещаются проекции точки?
8. Какая из проекций отрезка прямой линии не изменяет своей величины?
9. Можно ли путем поворота определить длину отрезка прямой линии и угол ее наклона к пл. H и к пл. V?
10. Можно ли показать на чертеже поворот, например, прямой вокруг оси, перпендикулярной к пл. H или пл. V, не изображая самой оси? На чем основан такой прием?
11. Какое название встречается для вращения без изображения оси?
12. Что понимается под названием «способ совмещения»?
13. Что понимается под названием «подъем в пространство»?
14. Как определить натуральную величину отрезка прямой общего положения и ее углы с пл. H и с пл. V?
15. Как определить расстояние от точки до прямой общего положения?
16. Как определить расстояние между двумя параллельными плоскостями, между двумя параллельными прямыми, между скрещивающимися прямыми?
ЛИТЕРАТУРА
Основная литература
1. Гордон В. О. Курс начертательной геометрии /В.О. Гордон, М.А. Семенцо-Огиевский; Под ред. В.О. Гордона.-25-е изд., стер. - М. : Высш.шк. , 2003 г.
2. Гордон В. О. Сборник задач по курсу начертательной геометрии /В.О. Гордон, Ю.Б. Иванов, Т.Е. Солнцева; Под ред. В.О. Гордона.-9-е изд., стер. - М. : Высш.шк. , 2003 г.
3. Курс начертательной геометрии /Под ред. В.О. Гордон. -24-е изд, стер. – М. : Выcшая школа , 2002 г.
4. Начертательная геометрия /Под ред. Н.Н.Крылова.-7-е изд., перераб. и доп.- М. : Выcшая школа , 2000 г.
5. Начертательная геометрия. Инженерная и машинная графика: Программа, контрольные задания и методические указания для студентов-заочников инженерно-технических и педагогических спец-тей вузов / Чекмарев А. А. , Верховский А. В. , Пузиков А. А. Под ред. А.А. Чекмарева.-Изд. 2-е, испр.- М. : Выcшая школа , 2001 г.
Дополнительная литература
6. Фролов С.А. Начертательная геометрия.- М.: Машиностроение,1978.
7. Бубенников А.В., Громов М.Я. Начертательная геометрия. – М.: Высшая школа, 1973.
8. Начертательная геометрия /под общей ред. Ю.Б. Иванова.- Минск: Вышейшая школа, 1967.
9. Боголюбов С.К. Черчение: Учебник для машиностроительных специальностей средних специальных учебных заведений. – 3-е изд., испр. и дополн. – М.: Машиностроение, 2000.
СОДЕРЖАНИЕ
Введение
Способы преобразования проекции
Способ замены плоскостей проекций
Способы вращения
Вопросы для самопроверки
Литература
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.