Часто для приведения прямой, плоской фигуры или пространственной формы в то частное положение, которое требуется для решения задачи, приходится заменять обе плоскости проекций. Переход от заданной системы плоскостей V/H к новой V1/H1 может быть осуществлен по одной из приведенных ниже схем:
V/H → V1/H → V1/H1 или V/H → V/H1 → V1/H1.
На рисунке 12 задана точка A в системе V/H. Затем осуществлен переход от системы V/H к системе V1/H1: проведена новая ось проекций Х1, найдена новая проекция а'1 точки А. Далее система V1/H заменена новой системой плоскостей проекции V1/H1 —вместо горизонтальной плоскости проекций введена новая плоскость Н1.
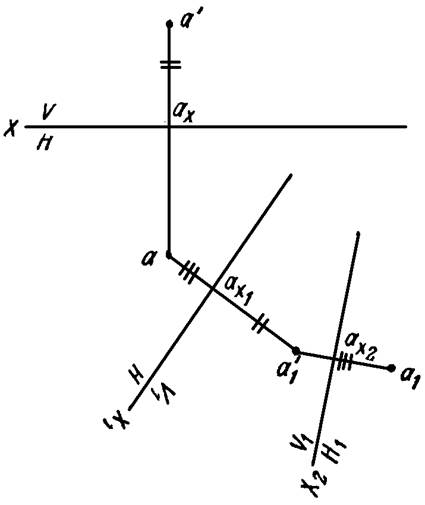
Рисунок 12
Положение новых осей проекций выбирается в соответствии с конкретными условиями задачи.
Рассмотрим примеры.
Пример 6. Определить истинную фигуру треугольника ABC (рисунок 13).
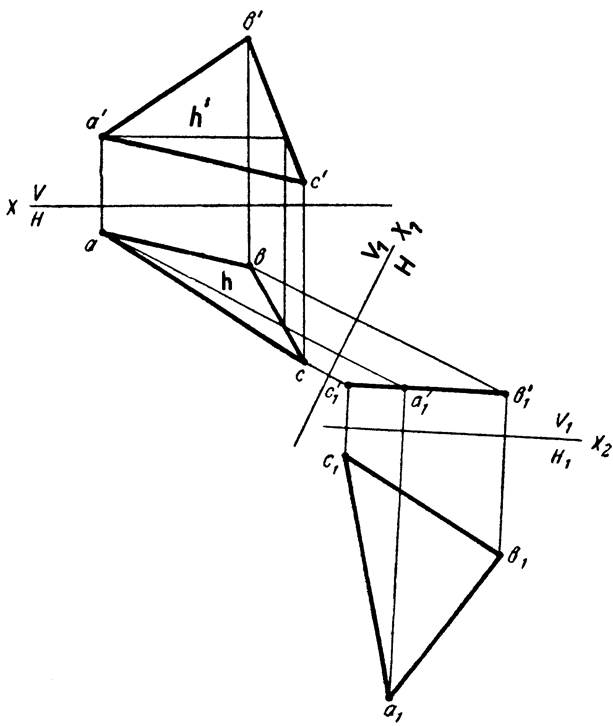
Рисунок 13
Треугольник спроектируется в натуральную величину на какую-либо плоскость проекций, если он окажется параллельным этой плоскости. Для того чтобы треугольник АВС оказался параллельным одной из плоскостей проекций, необходимо выполнить двойную замену плоскостей.
Сначала заменим плоскость V на плоскость V1. Плоскость V1 выберем перпендикулярно плоскости треугольника АВС — новая ось проекций x1должна быть перпендикулярна горизонтальной проекции горизонтали h. На новую фронтальную плоскость проекций треугольник cпроектируетcя в виде прямой линии c’1a’1b’1. Затем введем новую плоскость проекций H1 параллельно плоскости треугольника.
Горизонтальная проекция a1b1c1 треугольника ABC в новой системе — истинная величина его.
Пример 7. Дана пирамида SАВС (рисунок 14). Определить величину двугранного угла при ребре АВ.
Задача сводится к построению проекции данного угла на плоскость проекций, перпендикулярную к его ребру.
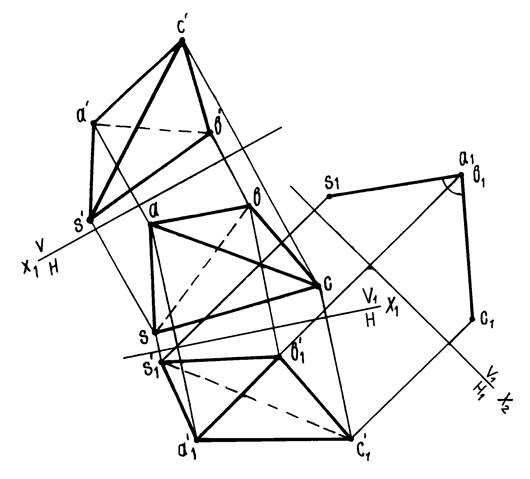
Рисунок 14
Так как ребро АВ — прямая общего положения, то необходимо произвести две последовательные замены плоскостей проекций. Плоскость V заменяем плоскостью V1, параллельной отрезку АВ.
Находим новую фронтальную проекцию s’1a’1b’1c’1 пирамиды SАВС на новой фронтальной плоскости проекций. Затем от системы V1/H перейдем к системе V1/H1. Плоскость H1 расположим перпендикулярно отрезку АВ. На плоскость Н1 ребро АВ спроектируется в точку, а грани SАВ и САВ — в прямые. Угол s1a1c1 будет искомым.
Пример 8. Дана пирамида SАВС (рисунок 15). Определить кратчайшее расстояние между ребрами SА и ВС.
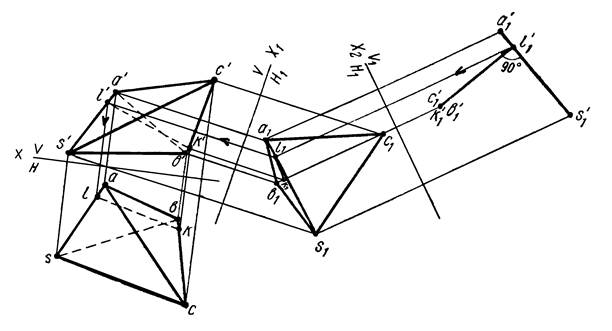
Рисунок 15
Прямые SА и ВС являются скрещивающимися. Следовательно, задача сводится к определению кратчайшего расстояния между двумя скрещивающимися прямыми. Для решения задачи необходимо произвести такую замену плоскостей проекций, чтобы в новой системе одна из прямых, например ВС (рисунок 16), оказалась перпендикулярной к какой-либо плоскости проекций. Замену плоскостей проекций осуществляем по схеме V/H → V/H1 → V1/H1.
Следовательно, решение задач методами преобразования сводится к выполнению четырех основных этапов:
1) преобразование прямой общего положения в прямую уровня (определение углов наклона прямой к плоскостям проекций и натуральной величины отрезков);
2. преобразование прямой уровня в проецирующую прямую (определение величины двугранного угла, расстояния между прямыми);
3. преобразование плоскости общего положения в проецирующую плоскость (определение углов наклона плоскости к плоскостям проекций, расстояния от точки до плоскости);
4. преобразование плоскости проецирующей в плоскость уровня (определяется натуральная величина плоскости).
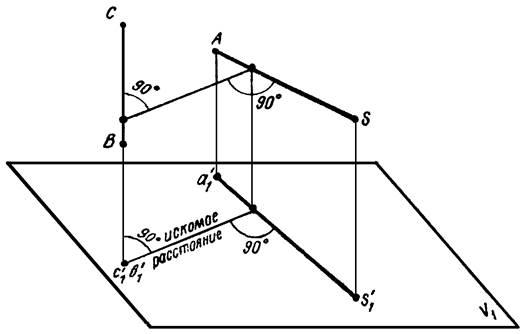
Рисунок 16
В системе V1H1 прямая ВС (см. рисунок 15) проектируется в точку. Отрезок k’1l’1 — кратчайшее расстояние между ребрами АS и ВС. Для построения проекций кратчайшего расстояния в системе V/H находим по линии связи точку l1 и проводим l1k1 параллельно оси проекций Х2 , после чего при помощи линий связи находим основные проекции kl и k’l’.
СПОСОБЫ ВРАЩЕНИЯ
Сущность способов вращения заключается в том, что заданная геометрическая форма путем вращения вокруг некоторой оси перемещается в пространстве до тех пор, пока она не займет частное положение по отношению к неизменной системе плоскостей проекций.
В зависимости от положения оси вращения по отношению к плоскостям проекций различают следующие способы вращения:
а) вращение вокруг осей, перпендикулярных к плоскостям проекций;
б) то же без указания положения осей вращения;
в) вращение вокруг горизонтали или фронтали;
г) вращение вокруг одного из следов плоскости (совмещение).
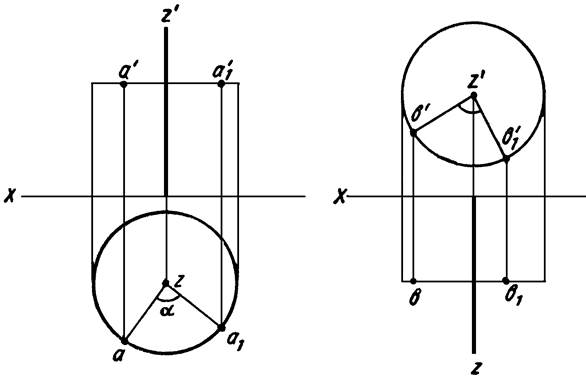
Рисунок 17 Рисунок 18
На эпюре (рисунок 17) изображена точка А и ось вращения Z, перпендикулярная к плоскости проекций H. При вращении вокруг оси Z точка А будет перемещаться по окружности, лежащей в плоскости, перпендикулярной оси вращения (параллельной плоскости проекций H). Если точку А переместить из положения А в положение A1 т. е. повернуть ее вокруг оси Z, на некоторый угол α , то ее горизонтальная проекция (а) займет положение a1, описав при этом дугу радиуса za (za — радиус вращения), а фронтальная проекция (а') точки переместится по прямой a’a’1, параллельной оси X.
Если ось вращения Z (рисунок 18) перпендикулярна к плоскости проекций V, то при вращении точки В вокруг этой оси фронтальная проекция траектории её перемещения будет окружностью, а горизонтальная — прямой, параллельной оси X.
Рассмотрим пример.
Пример 9. Совместить точку А с плоскостью Р путем вращения ее вокруг заданной оси Z (рисунок 19).
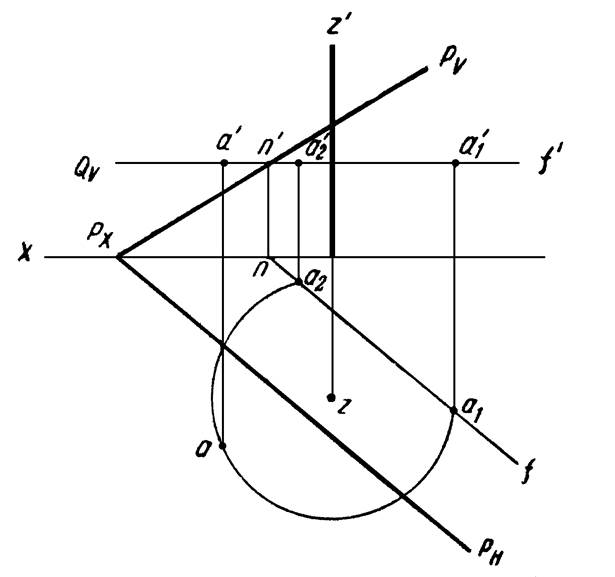
Рисунок 19
При вращении вокруг оси Z, точка А опишет окружность в плоскости Q, перпендикулярной этой оси. Плоскость Q пересечет заданную плоскость Р по горизонтали NF. Очевидно, точка А окажется в плоскости Р тогда, когда окружность, описываемая точкой А, пересечет горизонталь NF. Задача, как видно из чертежа, имеет два решения.
Чтобы повернуть прямую АВ (рисунок 20) на некоторый угол α, достаточно повернуть на заданный угол две принадлежащие, ей точки. Из чертежа видно, что треугольники abz и a1b1z1 равны между собой (по двум сторонам и углу между ними), а из их равенства следует, что ab = a1b1, т. е. величина горизонтальной проекции отрезка при вращении его вокруг оси, перпендикулярной Н, не изменяется, изменяется только ее положение относительно оси проекций. Это обстоятельство позволяет упростить построения при решении приведенного примера
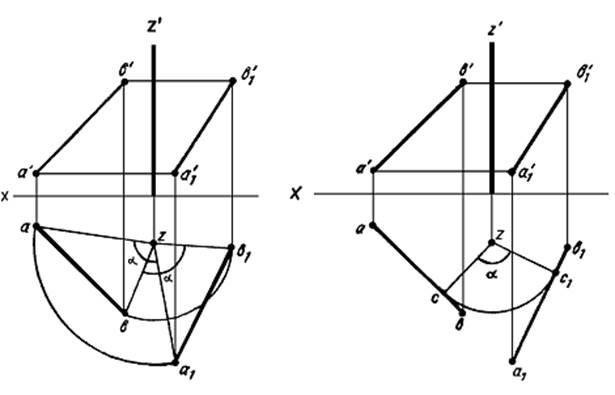
Рисунок 20 Рисунок 21
На рисунке 21 для поворота прямой АВ вокруг оси Z на угол α из z, опущен перпендикуляр на ab. Затем точка с повернута на заданный угол α, через точку c1 проведена прямая, перпендикулярная радиусу c1z, и отложены отрезки c1a1=са и c1b1=cb.
Вращение плоскости вокруг оси, перпендикулярной плоскости проекций, осуществляется путем вращения на один и тот же угол в одном и том же направлении точек и прямых, которыми задана плоскость.
На рисунке 22 плоскость, заданная треугольником АВС, повернута вокруг оси Z. в положение, перпендикулярное фронтальной плоскости проекций (горизонтальная проекция горизонтали А1 заняла положение, перпендикулярное оси X).
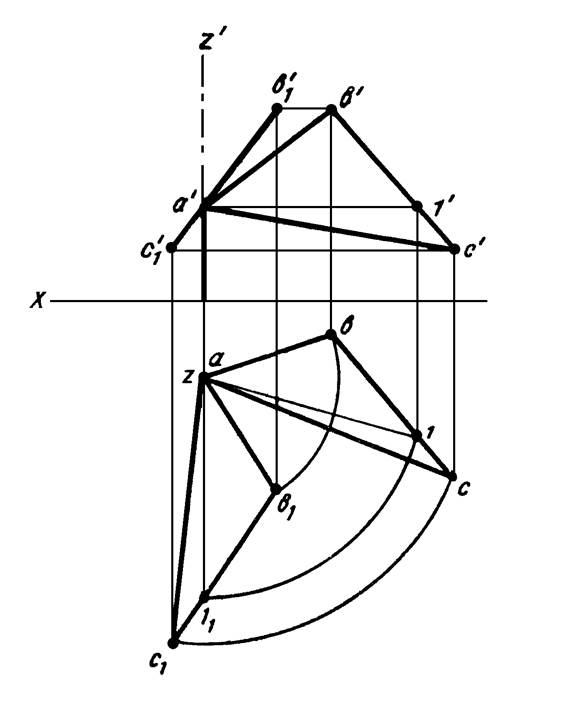
Рисунок 22
Если же плоскость задана следами, то для поворота плоскости на некоторый угол необходимо повернуть на заданный угол один из ее следов и горизонталь или фронталь этой плоскости (рисунок 23).
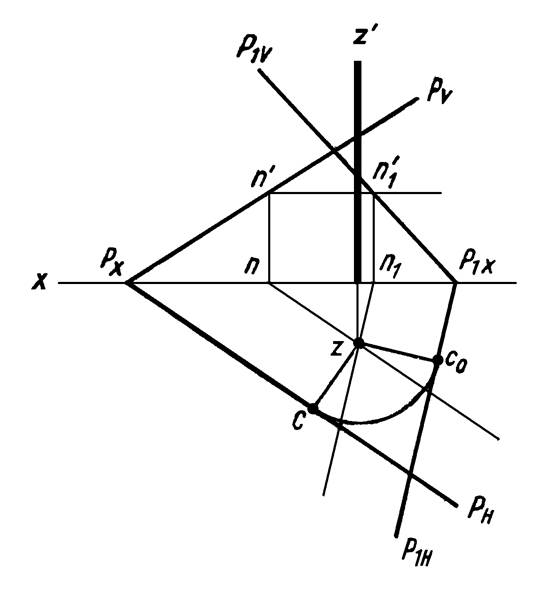
Рисунок 23
Таким образом, при вращении любой пространственной формы около оси, перпендикулярной одной из плоскостей проекций, проекция ее на эту плоскость по своей величине не изменится. Изменится лишь положение этой проекции относительно оси проекций. Пользуясь этим, для решения той или иной задачи можно применять способ вращения, не изображая на чертеже осей вращения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.