Методические рекомендации к контрольной работе по дисциплине "Высшая математика"

Методические рекомендации

к контрольной работе № 10

Для успешного выполнения контрольного задания необходимо знать:

1.  Что такое числовой ряд, общий член ряда, частичная сумма ряда, его остаток, сумма.

2.  Какие ряды называют сходящимися и какие основные задачи возникают при исследовании числовых рядов.

3.  В чем заключается необходимое условие сходимости числового ряда.

4.  На какие виды, в зависимости от знака членов ряда, принято разделять числовые ряды.

5.  Какой ряд называют обобщенным гармоническим и при каких значениях показателя обобщенный гармонический ряд сходится.

6.  Какой ряд называют геометрической прогрессией и при каких значениях знаменателя прогрессии она имеет конечную сумму.

7.  Как формулируются достаточные условия сходимости знакопостоянных рядов в признаке сравнения (предельная форма), в признаке Даламбера, в признаке Коши, в интегральном признаке.

8.  Какие виды сходимости различают для знакопеременных рядов.

9.  Какие условия являются достаточными для условной сходимости знакочередующегося ряда.

10.  Какие ограничения на остаток знакочередующегося ряда накладывает теорема Лейбница о достаточных условиях сходимости ряда.

11.  Какие достаточные признаки можно использовать для исследования знакопеременного числового ряда на абсолютную сходимость.

12.  Какой ряд называют функциональным и что понимают под областью сходимости функционального ряда. Какие основные задачи возникают при исследовании функциональных рядов.

13.  Какие виды сходимости различают для функциональных рядов.

14.   Какие ряды называют степенными. Какова структура области сходимости степенного ряда.

15.  Какие достаточные признаки можно использовать для нахождения радиуса сходимости степенного ряда. Как найти радиус сходимости.

16.  Какими свойствами обладает степенной ряд и его сумма внутри интервала сходимости.

17.  Какой ряд называется рядом Тейлора (рядом Маклорена) данной функции.

18.  Какие условия являются достаточными для того, чтобы ряд Тейлора (ряд Маклорена) данной функции сходился к ней.

Кроме теоретических знаний, для успешного выполнения контрольного задания необходимо владеть техникой нахождения пределов, уметь вычислять производные, включая производные сложных функций, и уметь раскладывать в ряд Тейлора такие элементарные функции, как

, , , , ,

,    .

ПРИМЕР РЕШЕНИЯ ТИПОВОГО ВАРИАНТА ЗАДАНИЯ

1. Выписать члены  , , и  ряда .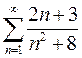

Решение. Как правило, числовой ряд задается формулой общего члена, которая определяет произвольный член ряда  как функцию его номера . В нашем случае формула общего члена имеет вид:

.                                              

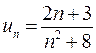Чтобы найти член ряда с фиксированным номером, надо подставить этот номер в формулу вместо  и выполнить указанные действия. Подставляя в по очереди , получим:

,,.         

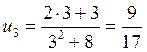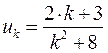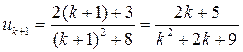2. Записать ряд, используя знак суммы :

                                                                         

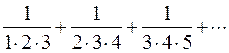
Решение. Чтобы выполнить данное упражнение, необходимо выявить математические закономерности в поведении выписанных членов ряда, затем, на основе этих закономерностей, сформулировать правила, по которым записывается член ряда с произвольным номером , и, наконец, записать формулу общего члена ряда.

Рассматривая выражение , легко заметить, что первый сомножитель в знаменателе каждого слагаемого совпадает с номером этого слагаемого, второй сомножитель на единицу больше первого, а третий – на единицу больше второго. Таким образом, знаменатель -го члена ряда должен иметь вид:

.

Тогда ряд запишется в виде

.          

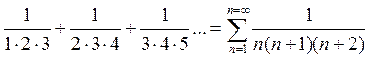3. Исследовать знакоположительный ряд на сходимость:

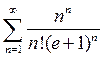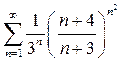             а) ,       б) ,       в) .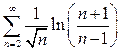       

Решение. а) При исследовании рядов, содержащих факториалы, удобно применять признак Даламбера. Мы получим:

,        ,       .

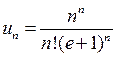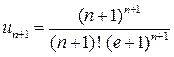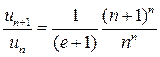Следовательно, предел Даламбера будет равен:

.        

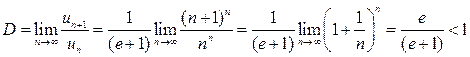Заметим, что при вычислении предела использовался второй замечательный предел:

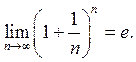
Поскольку предел Даламбера получился меньше единицы, исследуемый ряд сходится.

б) Если -ый член ряда является -ой степенью некоторого выражения, для исследования сходимости ряда удобно применять признак Коши. В данном случае имеем:

              

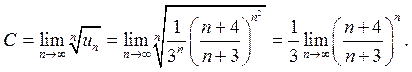
Чтобы вычислить предел , проведем замену . Мы получим:

.         

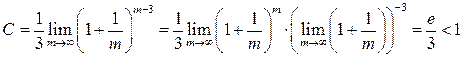Так как предел меньше единицы, то рассматриваемый ряд сходится.

в) Если попытаться исследовать ряд (в) с помощью признака Даламбера, то соответствующий предел будет равен единице. Другими словами, признак Даламбера не дает ответа на вопрос о сходимости данного ряда. Если воспользоваться признаком Коши, то результат будет тот же. Чтобы решить вопрос о сходимости ряда (в), рассмотрим поведение членов ряда при . С этой целью перепишем -ый член ряда в виде:

      

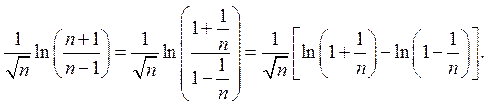
При  логарифм 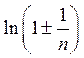 есть величина бесконечно малая эквивалентная . Поэтому при  

 .                    

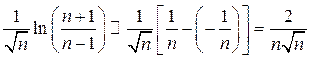Теперь ясно, что ряд (в) следует сравнить с рядом, у которого формула общего члена имеет вид:

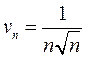,          или        .                          

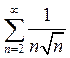Ряд представляет собой сходящийся обобщенный гармонический ряд с показателем . Применяя к рядам (в) и признак сравнения в предельной форме и учитывая, что при вычислении пределов бесконечно малые величины можно заменять им эквивалентными, будем иметь:

.                                        

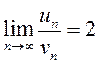Так как предел конечен и ряд сходится, то ряд (в) также сходится.

4. Исследовать знакочередующийся ряд на сходимость:

.                                      

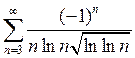Решение. Исследуем ряд на абсолютную сходимость, применяя интегральный признак. Рассмотрим функцию:

,              ,          

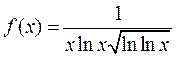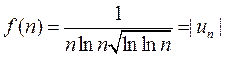которая принимает положительные значения и монотонно убывает на промежутке . Несобственный интеграл от этой функции по промежутку  имеет вид:

.                   

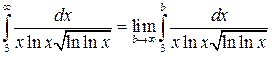Замечая, что

,

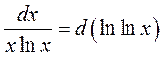перепишем интеграл в виде:

.    

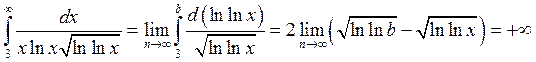Поскольку несобственный интеграл расходится, ряд не является абсолютно сходящимся рядом.

С помощью признака Лейбница исследуем ряд на условную сходимость. Так как последовательность  монотонно возрастает на промежутке , то члены ряда монотонно убывают по абсолютной величине с увеличением номера , причем

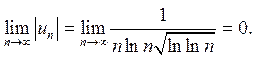
Поскольку в данном случае оба условия теоремы Лейбница выполняются, ряд сходится условно.

5.    Найти интервал сходимости степенного ряда и исследовать сходимость ряда на концах интервала:

                                       

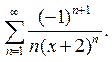
Решение. Применим признак Даламбера к ряду, составленному из абсолютных величин членов ряда , и потребуем, чтобы предел Даламбера был меньше единицы. Мы получим:

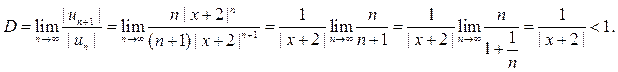
Из последнего неравенства следует, что ряд абсолютно сходится, если , или, что то же самое, для всех значений . При этом для всех , где - сколь угодно малое положительное число, ряд сходится равномерно.

Исследуем поведение ряда на границе области сходимости. При  ряд переходит в расходящийся гармонический ряд:

.

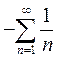При  ряд принимает вид:

.                                       

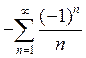Знакочередующийся ряд сходится условно по признаку Лейбница. Таким образом, область сходимости ряда имеет вид . Заметим, что на расширенной числовой прямой область сходимости ряда представляет собой интервал с центром в бесконечно удаленной точке .

6.    Написать три первых отличных от нуля члена разложения в ряд по степеням  функции:

.                                     

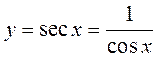Решение. Ряд Маклорена для функции  имеет вид:

.                                    

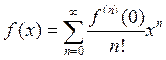Последовательно вычисляя производные, будем иметь:

 ,                                       

, ,                               

, ,               

,

,                                         

,

.                                       

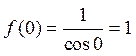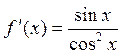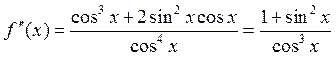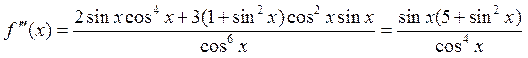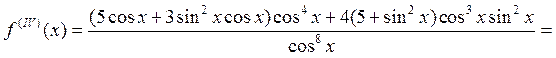
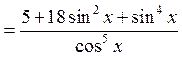Подставляя значения функции и ее производных при  в формулу и оставляя лишь слагаемые до номера  включительно, окончательно получим:

.                      

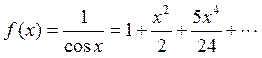7.    Используя разложение подынтегральной функции в ряд Тейлора, вычислить определенный интеграл с указанной точностью :

,                          .                            

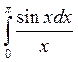Решение. Подставим под знак интеграла известное разложение функции  по степеням  

.                                  

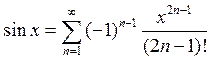Мы получим: .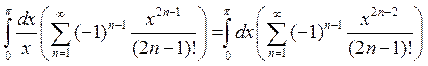     

Исследуя сходимость степенного ряда, записанного в правой части равенства , с помощью признака Даламбера, легко показать, что радиус сходимости ряда . Так как внутри интервала сходимости всякий степенной ряд сходится равномерно, в правой части выражения знаки интегрирования и суммирования можно поменять местами и выполнить почленное интегрирование. Результат интегрирования выражается в виде суммы знакочередующегося ряда:

.

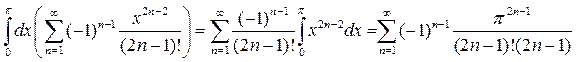Из теоремы Лейбница следует, что частичная сумма знакочередующегося ряда  отличается от полной суммы этого ряда  на величину меньшую, чем -ый член ряда,

.                                           

Таким образом, чтобы получить значение интеграла с заданной точностью , необходимо путем перебора слагаемых найти член ряда, для которого модуль.

Вычисляя члены ряда (30), будем иметь:

,  ,  ,  .

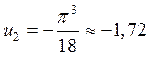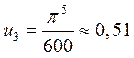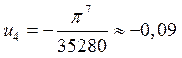Поскольку , интеграл с заданной точностью  будет равен:

.

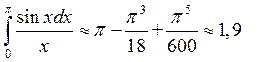РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1.  Высшая математика для экономистов / Под ред. проф. Н. Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1997. – 439 с.

2.  Общий курс высшей математики для экономистов / Под ред. проф. В. И. Ермакова. – М.: ИНФРА-М, 1999. – 650 с.

3.  Шипачев В. С.Высшая математика / Под ред. акад. А. Н. Тихонова. – М.: Высшая школа, 1985. – 426 с.

4.  Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. II. – 4-е изд., испр. и доп. – М.: Высшая школа, 1986. – 415 с., ил.