












ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
До сих пор мы изучали функции одной переменной y=f(x). На самом деле мир устроен сложнее, и не все можно описать с помощью функций одной переменной. Мы ограничимся изучением функций двух переменных, а затем распространим теорию на функции трех и более переменных
Опр. Множество называется связным, если любые две точки этого множества можно соединить непрерывной кривой, целиком принадлежащей этому множеству.
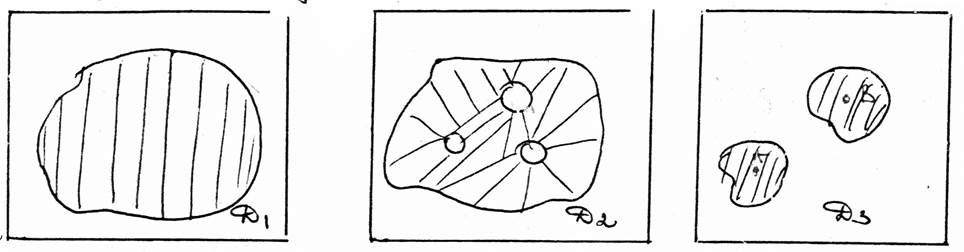
 D1 – связное множество (односвязно) D2 – связное множество (многосвязно) нет
D1 – связное множество (односвязно) D2 – связное множество (многосвязно) нет
Опр. Множество называется ограниченным, если существует круг с центром в начале координат, целиком содержащий данное множество.
(Можно рассматривать и прямоугольник, а не круг).
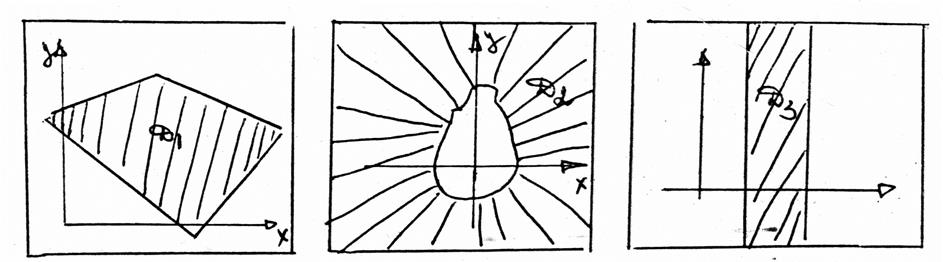
D1 – ограниченное множество D2 – нет D3 – нет
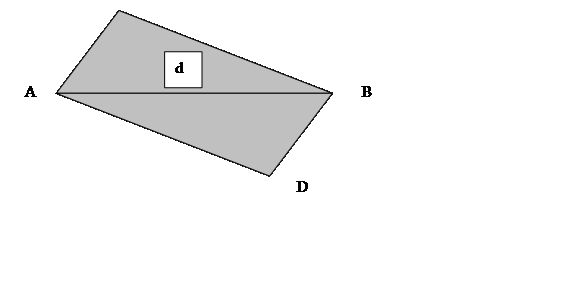
Опр. Диаметром множества называется наибольшее расстояние между парами точек данного множества.
Точки А и В множества D находятся друг от друга на расстоянии d – оно самое наибольшее из всех расстояний между двумя любыми точками множества D.
![]() ;
; ![]() .
.
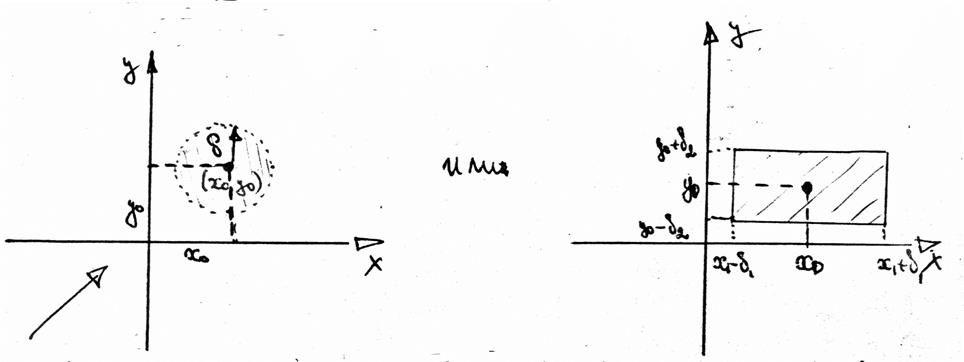
Рассматривается и окрестность с выколотым центром.
![]() - внешняя
точка
- внешняя
точка
![]() - внутренняя точка
- внутренняя точка
![]() - граничная точка
- граничная точка
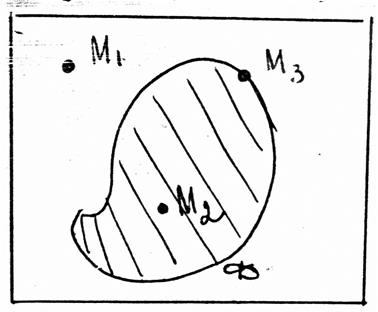
Опр. Точка М называется внутренней точкой множества, если она принадлежит множеству вместе с некоторой своей окрестностью.
Опр. Точка М называется граничной точкой множества, если в любой ее окрестности есть как точки, принадлежащие множеству, так и точки ему не принадлежащие.
Опр. Множество всех граничных точек данного множества образуют его границу.
Замечание: граничные точки множества могут и не принадлежать точкам множества.
Опр. Внешние точки это те, которые не являются ни внутренними, ни граничными.
Опр. Не пустое множество, все точки которого внутренние, называется открытым.
Опр. Не пустое множество, все граничные точки которого ему принадлежат, называется замкнутым.
Опр. Областью называется открытое связное множество.
Область вместе с границей образует замкнутую область.
Пусть дано два множества: R – множество действительных чисел и множество
![]() - множество упорядоченных пар
действительных чисел.
- множество упорядоченных пар
действительных чисел.
Опр. Если
каждому элементу множества Е по некоторому правилу или закону ставится в
соответствие вполне определенный элемент из R,
то говорят, что на множестве Е определена функция двух переменных х
и y ![]()
Множество Е – область определения функции
Способы задания функции: аналитический, графический, табличный и др.
Опр. Графиком
функции двух переменных ![]() называется
совокупность точек
называется
совокупность точек ![]() , то есть графиком является
поверхность в пространстве.
, то есть графиком является
поверхность в пространстве.
Как построить
график функции ![]() в п.д.с.к.?
в п.д.с.к.?
На плоскости ХОУ
изображается область определения Е. В каждой точке ![]() восстанавливаем перпендикуляр к
плоскости ХОУ и откладываем на нем значение
восстанавливаем перпендикуляр к
плоскости ХОУ и откладываем на нем значение ![]() .
Полученное таким образом множество точек пространства и будет графиком функции.
.
Полученное таким образом множество точек пространства и будет графиком функции.
Но не так
легко изображать поверхность на плоском листе. Поэтому для наглядности графика
функции ![]() вводят понятие линии уровня.
вводят понятие линии уровня.
Опр. Множество всех точек плоскости, для которых функция имеет одинаковое значение, называется линией уровня.
Уравнения
линий уровня т.о. ![]() , где
, где ![]() .
.
Пример:
Построить линии уровня ![]()
![]() - уравнения линий уровня
- уравнения линий уровня
![]() ,
, ![]() -
точка (0;0)
-
точка (0;0)
![]() ,
, ![]() -
окружность с центром в точке (0;0) и радиуса 1
-
окружность с центром в точке (0;0) и радиуса 1
![]() ,
, ![]() -
окружность с центром в точке (0;0) и радиуса
-
окружность с центром в точке (0;0) и радиуса ![]()
и т.д.
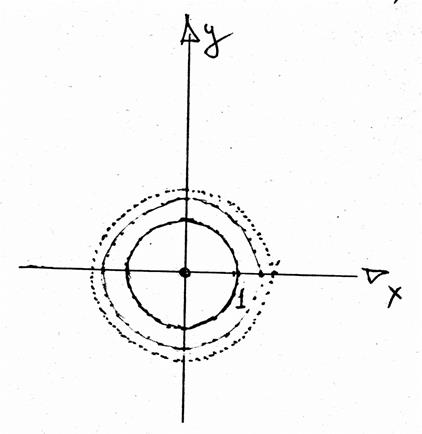
Таким образом,
поверхность ![]() представляет собой поверхность
вращения, так как линии уровня – концентрические окружности. Там где линии
уровня чаще, функция возрастает быстрее.
представляет собой поверхность
вращения, так как линии уровня – концентрические окружности. Там где линии
уровня чаще, функция возрастает быстрее.
Пример: Найти область определения функций:
а) ![]() ; б)
; б) 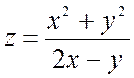
Решение:
а) ![]()
![]()
![]()
![]()
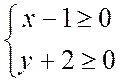 или
или
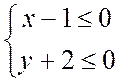
![]()
![]()
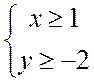 или
или
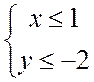
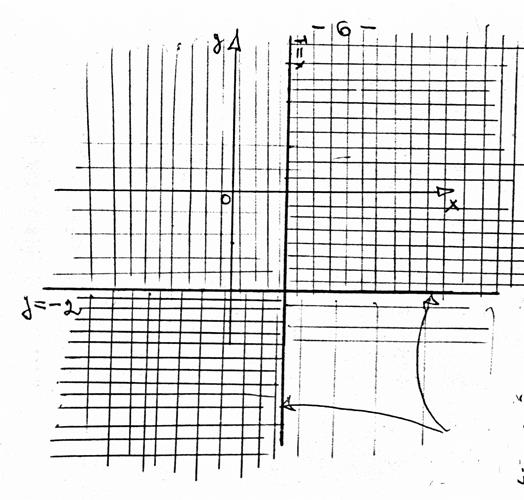 Ответ:
все точки плоскости, лежащие в вертикальных углах, образующихся прямыми
Ответ:
все точки плоскости, лежащие в вертикальных углах, образующихся прямыми ![]() и
и ![]() .
.
б) 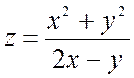
![]()
![]()
![]()
![]()
|
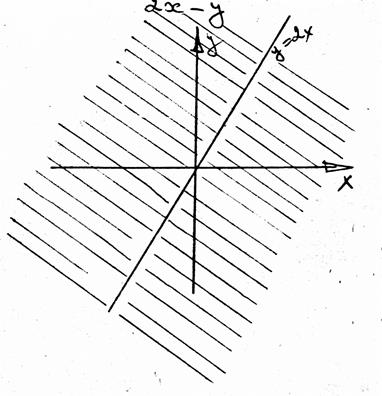
Ответ: все
точки плоскости кроме точек, лежащих на прямой ![]() .
.
Опр. Число
![]() называется пределом функции
называется пределом функции ![]() в точке
в точке ![]() ,
если для любого
,
если для любого ![]() , найдется такое
, найдется такое ![]() , что из условия: точка
, что из условия: точка ![]() является точкой
является точкой ![]() -окрестности т.
-окрестности т. ![]() с выколотым центром вытекает выполнение
неравенства
с выколотым центром вытекает выполнение
неравенства
![]()
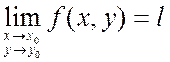
![]()
![]()
![]()
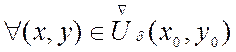
![]()
![]()
Из
определения, очевидно, что если предел функции в точке существует, то он не зависит
от пути следования т. ![]() к т.
к т. ![]() .
.
Пример 1:
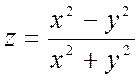 .
.![]()
Показать, что
функция не имеет предела в т. ![]() .
.
Решение:
Область
определения функции – все точки плоскости ХОУ, кроме т. ![]() .
.
Для того
чтобы убедиться, что в т. ![]() функция не имеет
предел, достаточно заметить, что при приближении переменной точки
функция не имеет
предел, достаточно заметить, что при приближении переменной точки ![]() к т.
к т. ![]() вдоль
биссектрисы 1-го координатного угла
вдоль
биссектрисы 1-го координатного угла ![]() значение функции
значение функции 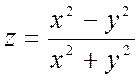 все время остается неизменным и
равным 0.
все время остается неизменным и
равным 0.
Если же
приближаться к т. ![]() вдоль каких-либо других
линий, то значения функции будут приближаться к другим числам. Так, например,
если двигаться вдоль положительной полуоси ОУ
вдоль каких-либо других
линий, то значения функции будут приближаться к другим числам. Так, например,
если двигаться вдоль положительной полуоси ОУ ![]() ,
то значение функции остается все время равным -1 (то есть во всех точках этой
полуоси
,
то значение функции остается все время равным -1 (то есть во всех точках этой
полуоси 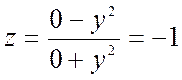 ).
).
Таким
образом, при приближении к точке ![]() по различным
путям функция стремится к различным значениям. Следовательно, функция не имеет
предела при
по различным
путям функция стремится к различным значениям. Следовательно, функция не имеет
предела при ![]() .
.
Аналогично тому, как это делалось для функции одной переменной, можно доказать, что и для функций двух переменных предел суммы двух функций равен сумме их пределов; предел произведения равен произведению пределов сомножителей; предел частного равен частному от деления предела числителя на предел знаменателя (при условии, что предел делителя отличен от нуля).
Отметим
также, что разность между функцией, имеющей предел, и ее пределом есть,
очевидно, бесконечно малая функция. (функция ![]() называется
бесконечно малой в точке, если ее предел в этой точке равен 0).
называется
бесконечно малой в точке, если ее предел в этой точке равен 0).
Опр.1 Функция
![]() называется непрерывной во внутренней
точке
называется непрерывной во внутренней
точке ![]() области Е, где определена
функция, если
области Е, где определена
функция, если 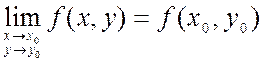 .
.
Если учесть,
что ![]() ,
, ![]() ,
,
![]() , то определение 1 перейдет в
, то определение 1 перейдет в
Опр. 2 Функция
непрерывна в точке ![]() , если приращение функции
, если приращение функции ![]() стремится к нулю, при стремлении к
нулю приращений
стремится к нулю, при стремлении к
нулю приращений ![]() и
и ![]() ,
то есть
,
то есть 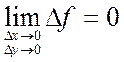 .
.
Опр. Функция
![]() называется непрерывной в области,
если она непрерывна в каждой точке области.
называется непрерывной в области,
если она непрерывна в каждой точке области.
Функции, непрерывные во всех точках некоторой замкнутой ограниченной области, обладают следующими свойствами, которые приведем без доказательств.
Т 1 (об
ограниченности функции) Функция ![]() , непрерывная в
замкнутой, ограниченной области, ограничена в этой области
, непрерывная в
замкнутой, ограниченной области, ограничена в этой области ![]() , т.е.
, т.е. ![]() ,
,
![]() .
.
Т 2 (о
наибольшем и наименьшем значениях функции) Непрерывная в замкнутой, ограниченной
области ![]() функция
функция ![]() принимает
в этой области наибольшее и наименьшее значения.
принимает
в этой области наибольшее и наименьшее значения.
Это означает,
что в данной области ![]() существуют точки
существуют точки ![]() и
и ![]() ,
что для всех точек
,
что для всех точек ![]() имеет место неравенства
имеет место неравенства
![]() и
и ![]()
Говорят, что
в точке ![]() функция
функция ![]() достигает
наибольшего значения в данной области, а в точке
достигает
наибольшего значения в данной области, а в точке ![]() -
наименьшего.
-
наименьшего.
Замечание: Если рассматривать функцию непрерывную не в замкнутой и ограниченной области, то Т 1 и Т2 могут оказаться неверными.
Т 3 (о
промежуточных значениях) Пусть функция ![]() непрерывна
в некоторой области
непрерывна
в некоторой области ![]() . Тогда каковы бы ни были
точки
. Тогда каковы бы ни были
точки ![]() и
и ![]() этой
области, для любого числа с, заключенного между
этой
области, для любого числа с, заключенного между ![]() и
и
![]() , существует в области
, существует в области ![]() такая точка
такая точка ![]() ,
что
,
что ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.