В
частности, если ![]() , а
, а ![]() ,
то в области
,
то в области ![]() найдется такая точка, в которой
значение функции равно нулю.
найдется такая точка, в которой
значение функции равно нулю.
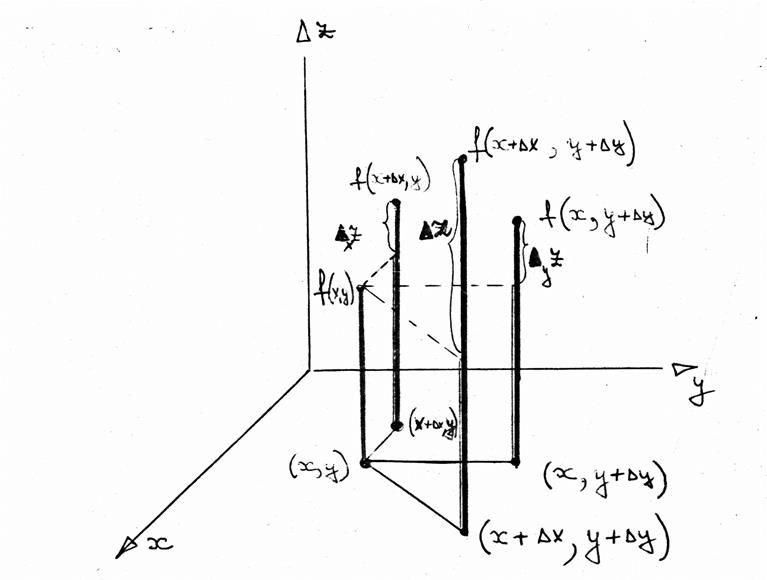
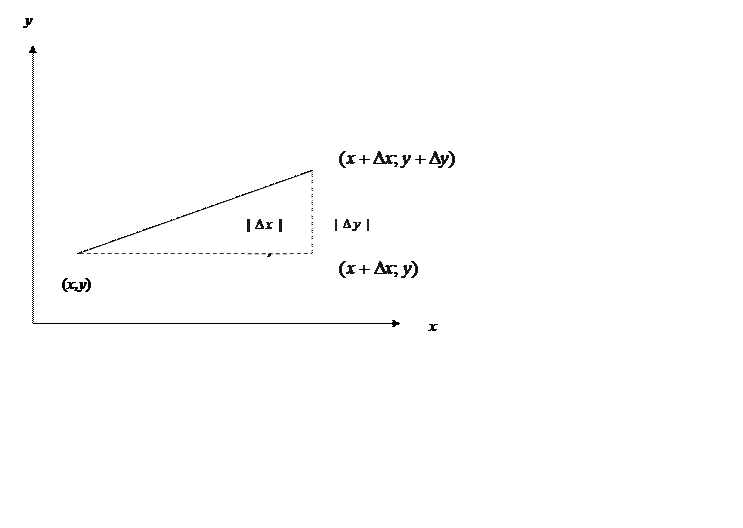
Пусть дана функция
![]() ,
, ![]() -
фиксированная точка,
-
фиксированная точка, ![]() - приращение первой
координаты,
- приращение первой
координаты, ![]() - приращение второй координаты
точки.
- приращение второй координаты
точки.
![]() - полное приращение функции,
- полное приращение функции,
![]() - приращение функции по Х,
- приращение функции по Х,
![]() - приращение функции по Y.
- приращение функции по Y.
См. чертеж
Опр. Частной
производной ![]() функции
функции ![]() называется
называется
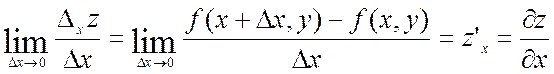 .
.
Аналогично 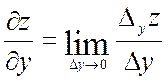
Примеры:
Найти частные производные функций
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) 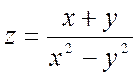 ; 4)
; 4) ![]() ; 5)
; 5)
![]() .
.
Решение:
1) ![]() - функция 2-х переменных х и y, поэтому 2-е частные производные
- функция 2-х переменных х и y, поэтому 2-е частные производные ![]() и
и ![]() (читается
так: зет штрих по икс или де зет по де икс)
(читается
так: зет штрих по икс или де зет по де икс)
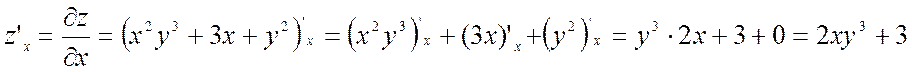 ;
;
![]() ;
;
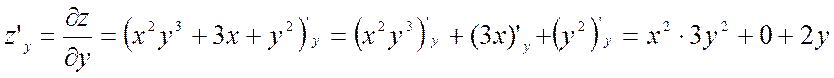 ;
;
![]() .
.
2) ![]() ;
; ![]()
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
3) 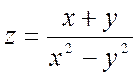 ;
; ![]()
![]()
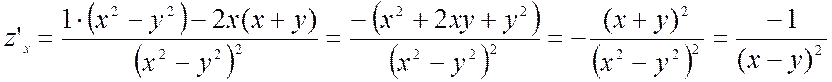 ;
;
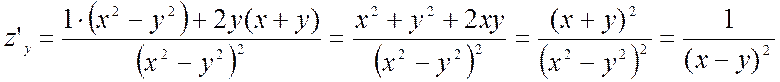 ;
;
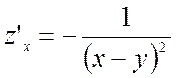 ;
; 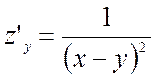 .
.
№ 4 и № 5 сделать самостоятельно.
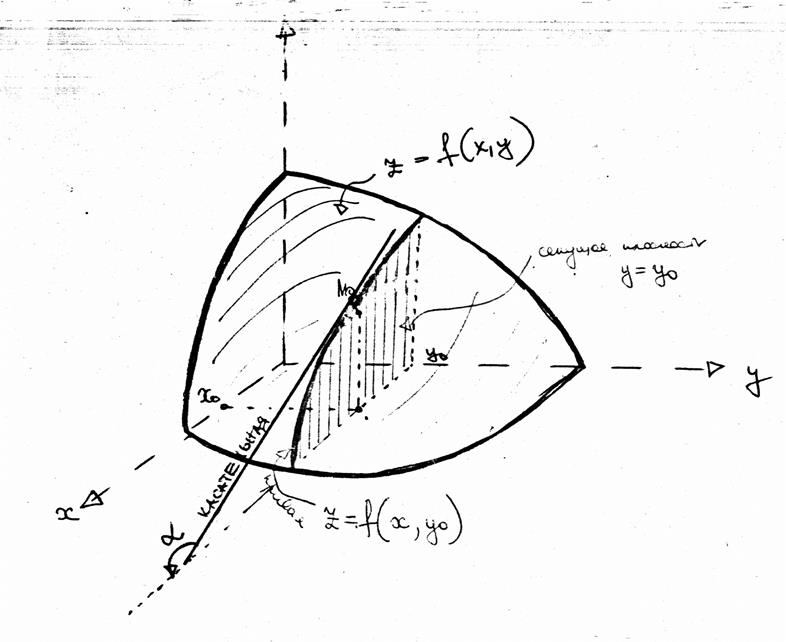
Частные производные функции 2-х переменных имеют простой геометрический смысл.
Зафиксируем значение y, положив ![]() . Тогда функция
. Тогда функция ![]() становится функцией только одной
переменной х. Мы получим график этой функции, если рассечем поверхность
становится функцией только одной
переменной х. Мы получим график этой функции, если рассечем поверхность ![]() плоскостью
плоскостью ![]() .
Исходя из геометрического смысла производной для функции одной переменной,
заключаем, что
.
Исходя из геометрического смысла производной для функции одной переменной,
заключаем, что ![]() есть тангенс угла
есть тангенс угла ![]() между осью ОХ и касательной,
проведенной в точке
между осью ОХ и касательной,
проведенной в точке ![]() к кривой, полученной от
сечения поверхности
к кривой, полученной от
сечения поверхности ![]() плоскостью
плоскостью ![]() .
.
Аналогично, ![]() есть ………………………… (написать самостоятельно).
есть ………………………… (написать самостоятельно).
 |
Опр. Функция
![]() называется дифференцируемой в точке
называется дифференцируемой в точке ![]() , если полное приращение функции в
этой точке может быть представлено в виде суммы 2х частей, одна из
которых линейно зависит от приращений аргументов
, если полное приращение функции в
этой точке может быть представлено в виде суммы 2х частей, одна из
которых линейно зависит от приращений аргументов ![]() и
и
![]() , а другая является б.м. более высокого
порядка по сравнению с
, а другая является б.м. более высокого
порядка по сравнению с ![]() .
.
![]() , где
, где ![]() при
при
![]() .
.
Выясним смысл А и В.
![]() ;
; 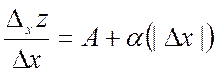 ;
;
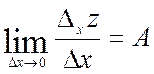
Т.о. 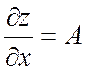 , аналогично
, аналогично 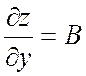
Т 1 (1ое
необходимое условие дифференцируемости) Если функция ![]() дифференцируема в точке
дифференцируема в точке ![]() , то она имеет в этой точке частные
производные, причем
, то она имеет в этой точке частные
производные, причем
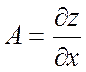 ;
; 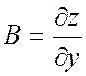 .
.
Т 2 (2ое
необходимое условие дифференцируемости) Если функция ![]() дифференцируема в точке
дифференцируема в точке ![]() , то она и непрерывна в этой точке.
, то она и непрерывна в этой точке.
Доказательство очевидно в силу определения дифференцируемости и свойств б. малых.
Т 3 (достаточное
условие дифференцируемости) Если функция ![]() имеет
в точке
имеет
в точке ![]() непрерывные частные производные, то
эта функция дифференцируема в точке
непрерывные частные производные, то
эта функция дифференцируема в точке ![]() .
.
б/д
Пусть функция
![]() дифференцируема по переменным х
и у, а функции
дифференцируема по переменным х
и у, а функции ![]() и
и ![]() -
дифференцируемы по переменным u,v.
-
дифференцируемы по переменным u,v.
Тогда функция
![]() дифференцируема по u и v,
причем
дифференцируема по u и v,
причем
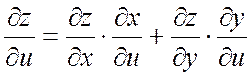 ;
; 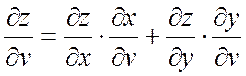
Доказательство.
Было введено ![]() ,
, ![]()
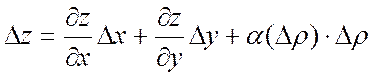 (это
следует из дифференцируемости функции
(это
следует из дифференцируемости функции ![]() )
)
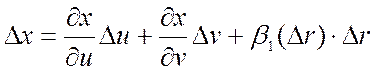
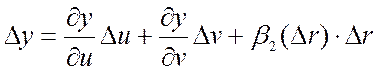 (по
условию
(по
условию ![]() и
и ![]() -
дифференцируемы).
-
дифференцируемы).
Тогда
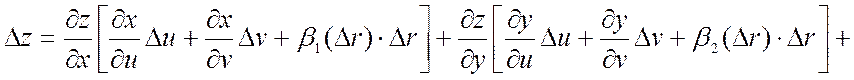
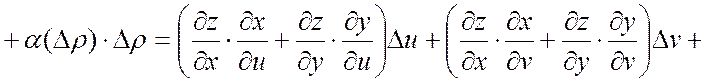
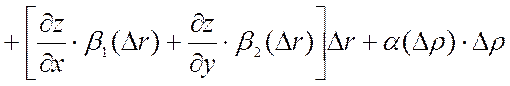 .
.
б.м. ![]()
Заметим, что
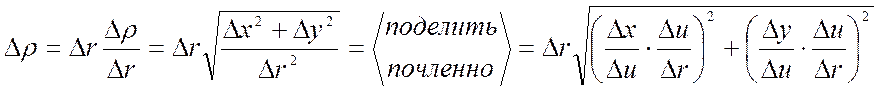 ,
где
,
где ![]() - ограничено (т.к.
- ограничено (т.к. 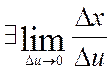 ) и
) и 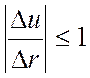 .
Поэтому первый квадрат под знаком корня ограничен. По той же причине ограничен
и второй квадрат. Тогда
.
Поэтому первый квадрат под знаком корня ограничен. По той же причине ограничен
и второй квадрат. Тогда ![]() , где
, где ![]() - ограниченная величина. Поэтому
- ограниченная величина. Поэтому ![]() , где
, где ![]() при
при
![]() .
.
б.м.![]()
Таким образом,
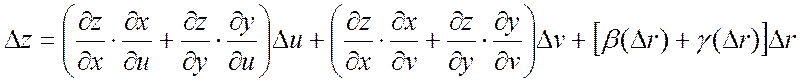 ч.т.д.
ч.т.д.
б.м.в.
Примеры:
1) ![]() , где
, где ![]()
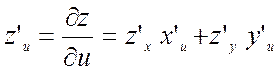
![]()
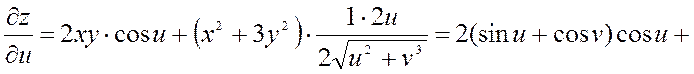
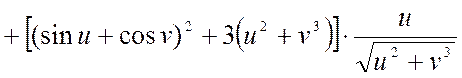
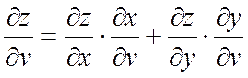
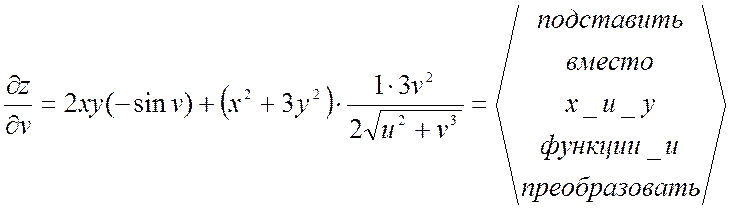
2) ![]() , где
, где ![]() ;
;
![]()
![]()
![]()
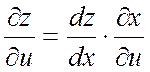 ;
;
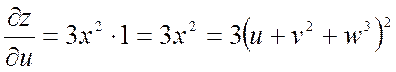 ;
;
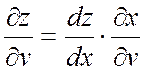 ;
;
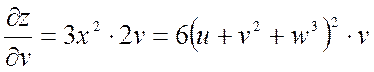 ;
;
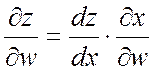 ;
;
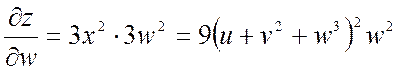 .
.
3) ![]() ,
, ![]() .
Найти
.
Найти ![]()
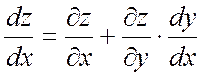 .
(Если
.
(Если ![]() подставим в данную функцию, тогда
подставим в данную функцию, тогда ![]() ).
).
Самостоятельно написать формулы для нахождения частных производных
4) ![]() , где
, где ![]() ,
,
![]()
5) ![]() , где
, где ![]() ,
,
![]()
6) ![]() , где
, где ![]() ,
, ![]() ,
, ![]()
Пусть дана
дифференцируемая функция ![]() , тогда по
определению дифференцируемости
, тогда по
определению дифференцируемости ![]() .
.
![]() гл.
часть
гл.
часть
Опр. Дифференциалом функции 2х переменных называется главная часть приращения функции, линейно зависящая от приращения аргументов
![]() или
или 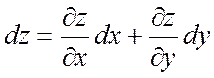 .
.
х, у
независимые переменные, тогда ![]() ,
, ![]() .
.
I. Пусть ![]() , где х и у
независимые переменные, тогда
, где х и у
независимые переменные, тогда 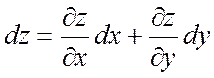 .
.
II. Пусть ![]() , где
, где ![]() ,
, ![]() .
Найдем в этом случае дифференциал
.
Найдем в этом случае дифференциал ![]() .
.
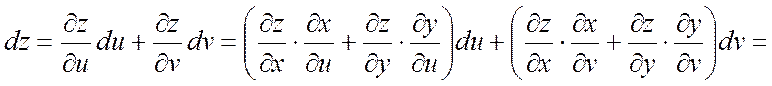
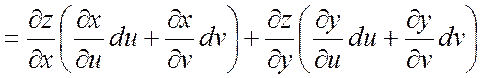
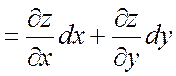
Отсюда следует, что форма дифференциала не изменилась.
1) ![]() ;
; ![]()
![]()
2) 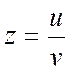 ;
; 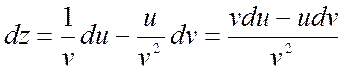
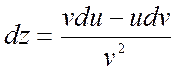
3) ![]() ;
; ![]()
Пусть дана
функция ![]() ,
, ![]() -
фиксированная точка,
-
фиксированная точка, ![]() - новая точка, где
- новая точка, где ![]() ,
, ![]() .
.
![]()
![]()
![]() .
.
Приращение
функции можно с достаточной степенью точности заменить дифференциалом, т.е. ![]() . Тогда
. Тогда
![]()
или
![]()
Пример.
Вычислить ![]() .
.
Решение.
Составим функцию ![]() . Нас интересует значение
этой функции в точке
. Нас интересует значение
этой функции в точке ![]() .
.
![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
![]() (оценку погрешности не делаем
здесь).
(оценку погрешности не делаем
здесь).
Пусть функция
![]() дифференцируема в точке
дифференцируема в точке ![]() . Тогда в достаточно малой
окрестности т.
. Тогда в достаточно малой
окрестности т. ![]() приращение функции
приращение функции ![]() можно приближенно заменить
дифференциалом
можно приближенно заменить
дифференциалом ![]() , то есть
, то есть
![]() или
или
![]() .
.
Функция, для
которой ![]() , линейная функция, ее график плоскость.
Эта плоскость называется касательной плоскостью к графику функции
, линейная функция, ее график плоскость.
Эта плоскость называется касательной плоскостью к графику функции![]() в точке
в точке![]() .
.
Уравнение касательной плоскости
![]()
Пример.
![]()
![]() .
.
Уравнение касательной плоскости
![]() или
или ![]() .
.
Теперь ничего не стоит составить уравнение нормали
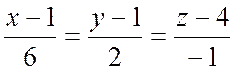 ;
; ![]() -
направляющий вектор нормали.
-
направляющий вектор нормали.
Таким образом уравнение нормали к графику дифференцируемой функции
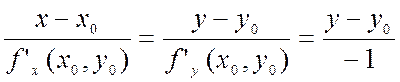
Производная 2го порядка есть производная от производной первого порядка
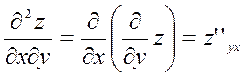 ;
; 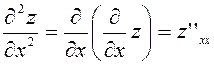 ;
;
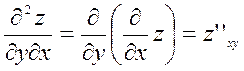 ;
; 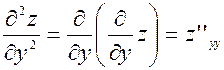
Пример.
![]()
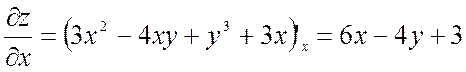 ;
; 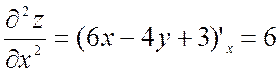 .
.
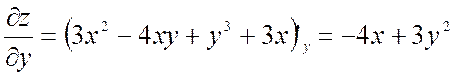 ;
; 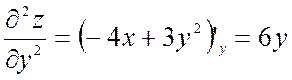 .
.
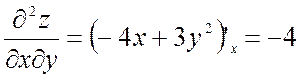 ;
; 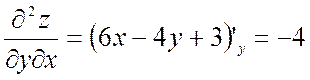 .
.
Теорема.
Если функция ![]() имеет в некоторой точке
непрерывные смешанные производные, то эти произведения равны между собой.
имеет в некоторой точке
непрерывные смешанные производные, то эти произведения равны между собой.
Пусть функция
![]() определена в некоторой области
определена в некоторой области ![]() .
.
Опр. Точка
![]() , являющаяся внутренней точкой
области определения функции
, являющаяся внутренней точкой
области определения функции ![]() , называется
точкой максимума, если существует такое положительное число
, называется
точкой максимума, если существует такое положительное число ![]() , что для всех точек
, что для всех точек ![]() выполняется неравенство
выполняется неравенство ![]() .
.
Определение минимума дать самостоятельно.
Теорема
Если точка ![]() является точкой ext дифференцируемой в этой точке функции
является точкой ext дифференцируемой в этой точке функции ![]() , то
, то ![]() и
и
![]() .
.
Опр. Точка, в которой частные производные равны 0, называется стационарной точкой функции.
Стационарные точки являются подозрительными на ext.
Пусть дана
дифференцируемая функция ![]() , точка
, точка ![]() принадлежит области
дифференцирования. Из условия, что
принадлежит области
дифференцирования. Из условия, что ![]() следует, что
следует, что
![]() и
и ![]()
Проведем
касательную плоскость к поверхности ![]() в т.
в т. ![]() .
.
 Ее уравнение
0 0
Ее уравнение
0 0
![]()
 Значит уравнение касательной
плоскости
Значит уравнение касательной
плоскости ![]() - это
горизонтальная плоскость (параллельна плоскости ХОУ).
- это
горизонтальная плоскость (параллельна плоскости ХОУ).
В точке ext касательная плоскость горизонтальна.
|
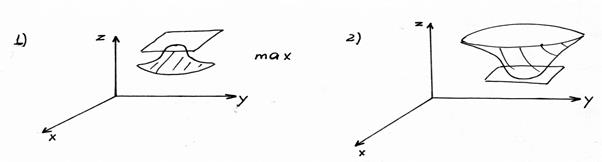
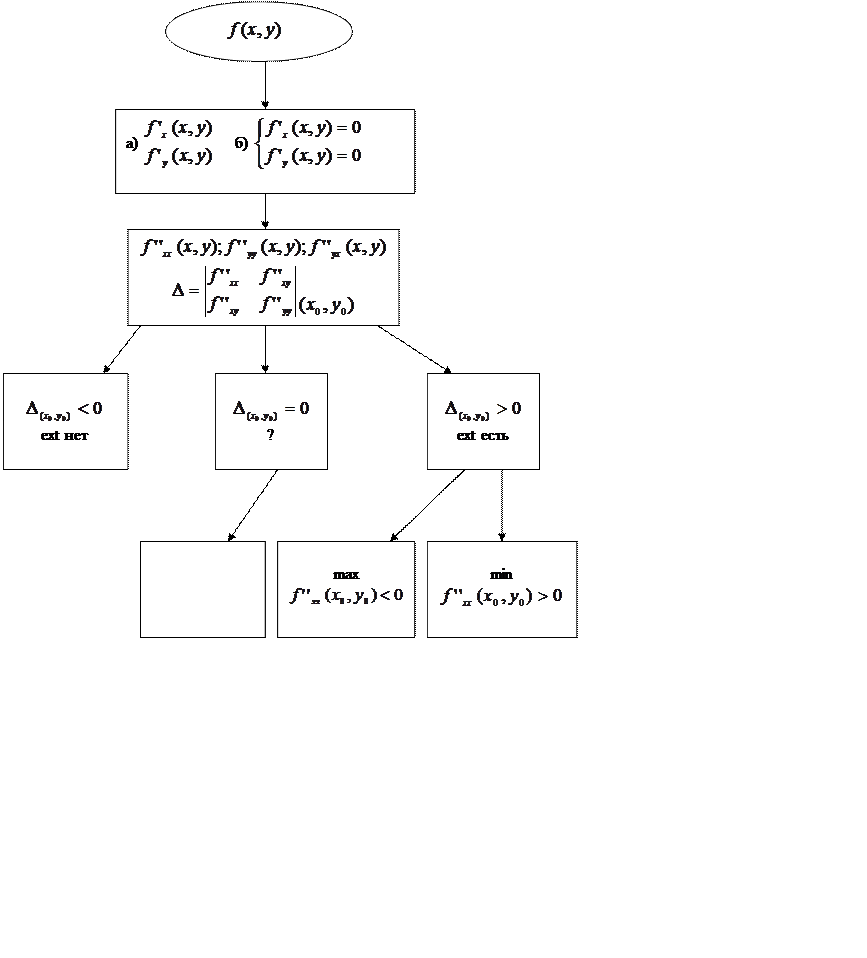
Теорема
(достаточное условие ext функции 2х
переменных) Пусть функция ![]() является дважды
дифференцируемой в стационарной точке
является дважды
дифференцируемой в стационарной точке ![]() .
Тогда если
.
Тогда если
I. Определитель 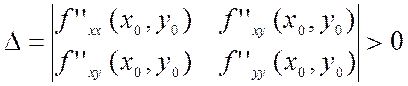 ,
то стационарная точка
,
то стационарная точка ![]() является точкой ext, а именно: а) точкой max, если
является точкой ext, а именно: а) точкой max, если ![]() и б) точкой min,
если
и б) точкой min,
если ![]() .
.
II. Если ![]() , то стационарная
точка
, то стационарная
точка ![]() не является точкой ext.
не является точкой ext.
III. В случае ![]() ничего
определенного сказать нельзя.
ничего
определенного сказать нельзя.
Замечание:
![]()
Пример.
Найти ext функции ![]()
I шаг ![]()
![]() ;
;
II шаг 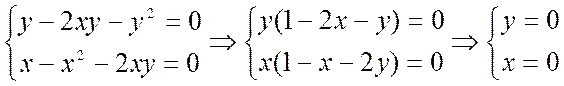 или
или
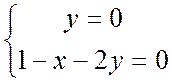
или 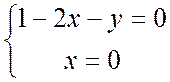 или
или
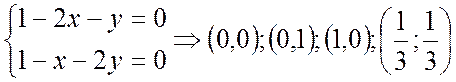 - стационарные точки.
- стационарные точки.
III шаг ![]() ;
;
![]() ;
; ![]()
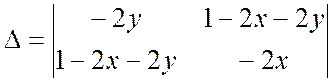 ;
;
![]() ext нет
ext нет
![]() ext нет
ext нет
![]() ext нет
ext нет
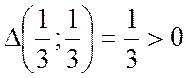 , ext есть.
, ext есть. 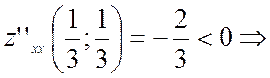 точка max
точка max 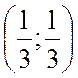 ,
,
а 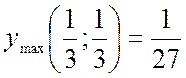 .
.
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.