Характеристики замкнутых САР и процессы в них

Лекция 4

(4 часа)

ХАРАКТЕРИСТИКИ ЗАМКНУТЫХ САР И ПРОЦЕССЫ В НИХ

Передаточные функции САР

по управляющему и возмущающему воздействию

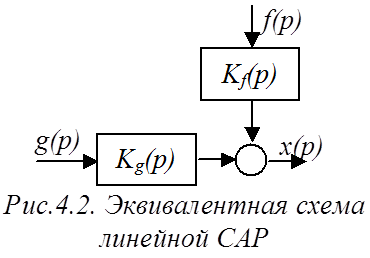
Обобщенная структурная схема линейной непрерывной стационарной САР представлена на рис.4.1.

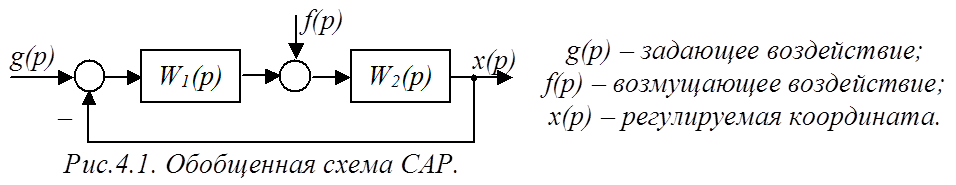
Структурная схема содержит два входа (воздействия) и один выход (регулируемая координата). Звено с ПФ W₁(p) полностью или частично соответствует регулятору, звено с ПФ W₂(p) – объекту управления (ОУ).

Введем понятия ПФ замкнутой САР по управляющему воздействию (по управлению)  и ПФ замкнутой САР по возмущающему воздействию (по возмущению) . Через эти ПФ регулируемая координата, согласно принципа суперпозиции, может быть выражена следующим образом:

              .                        (1)

При определении ПФ замкнутой САР по одному из воздействий другое воздействие принимается равным нулю. Так, полагая , находим ПФ по управлению:

          .

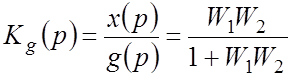Аналогично, полагая , находим ПФ по возмущению:

                    .

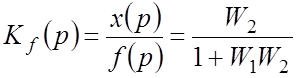Уравнение (1) позволяет схему САР изобразить в следующем виде (рис.4.2). Именно на этом основывается ранее упомянутый способ преобразования САР с несколькими входами, основанный на принципе линейности.

Параметры передаточных функций разомкнутых и замкнутых САР

В общем виде ПФ замкнутой САР может быть представлена как отношение двух операторов-многочленов:

         

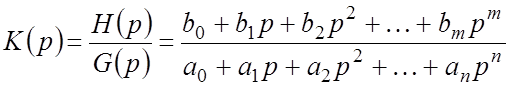
при  (условие физической реализуемости).

Параметр n называется порядком САР. Он соответствует порядку ДУ, описывающего работу системы во временной области.

Полином H(p) называется полиномом воздействия, полином G(p) – характеристическим полиномом замкнутой САР.

Полюсами ПФ называются точки (значения переменной p), при которых ПФ K(p) обращается в бесконечность. Полюса ПФ совпадают с нулями характеристического полинома G(p), то есть, с корнями уравнения

G(p)=0,

которое называется характеристическим уравнением замкнутой САР.

Нулями ПФ называются точки (значения переменной p), при которых ПФ K(p) обращается в нуль. Нули ПФ совпадают с нулями полинома воздействия H(p), то есть, с корнями уравнения

          H(p)=0.

По определению ПФ не может иметь кратных полюсов, то есть, все полюса должны быть простыми.

Передаточная функция разомкнутой САР также в общем виде может быть представлена как отношение операторов-многочленов:

          .

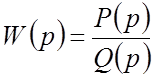Полином P(p) называется полиномом воздействия, полином Q(p) – характеристическим полиномом разомкнутой САР.

Уравнение

         

называется характеристическим уравнением разомкнутой САР.

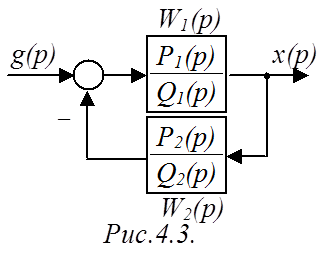
Рассмотрим САР, изображенную на рис.4.3. ПФ разом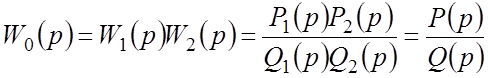кнутой САР:

          .

ПФ замкнутой САР:

.

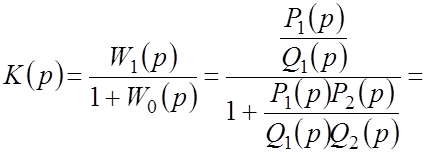
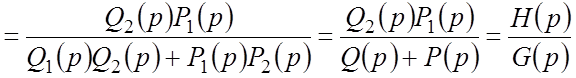Из последнего равенства следует то важное соотношение, что характеристический полином замкнутой САР равен сумме числителя и знаменателя ПФ разомкнутой САР:

          .

Отметим такое важное свойство полиномов: если все коэффициенты полинома – действительные числа, то в общем случае нулями его могут быть как действительные, так и комплексные числа, причем комплексные нули такого полинома (при их наличии) образуют комплексно-сопряженные пары.

Типовые воздействия

При анализе характеристик САР применяются следующие типовые воздействия (рис.4.4):

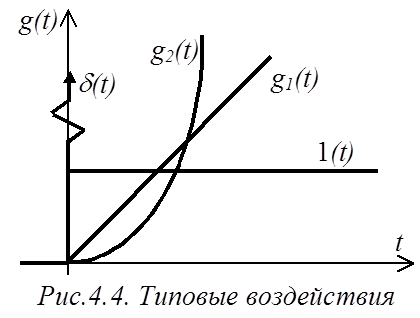1. Единичный скачок (единичная ступенчатая функция Хевисайда):

         

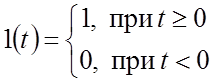
Такое воздействие имеет место в штатных режимах работы. Применительно к электромеханике этому типу воздействия соответствуют, например, режимы включения и отключения питания электродвигателей, режима наброса и сброса нагрузки.

2. Дельта-функция:

                   

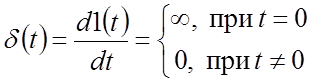
Физически эта функция описывает импульс бесконечно большой амплитуды и бесконечно малой продолжительности, ограничивающий площадь, равную единице.

Этому типу нагрузки соответствуют случаи внезапного увеличения нагрузки электродвигателей, например, при резке или распиловке материала, вызванные технологическим циклом (начало реза) или неоднородностью материала.

3. Полиномиальные воздействия вида

           

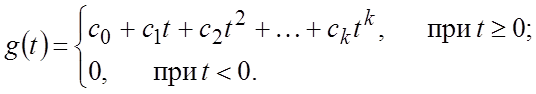
Частными случаями такого воздействия, например, являются:

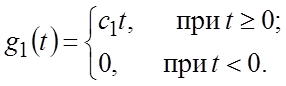              или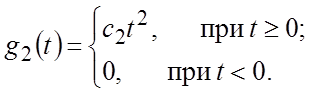 

Эти воздействия соответствуют случаям изменения управления с постоянной скоростью и с постоянным ускорением соответственно.

Такие воздействия имеют место в следящих системах.

Временные характеристики замкнутых САР,

их взаимосвязь и связь с передаточной функцией

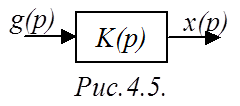Любая, сколь угодно сложная САР может быть представлена в виде, представленном на рис.4.5, и описана уравнениями в области изображений Лапласа:

              ,                                        (2)

где ;  .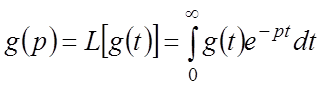

Напомним, что ПФ САР также является изображением некоторой операторной функции-оригинала:

.

Помимо ДУ и ПФ, в ТАУ при описании и анализе САР широко используют переходные функции и временные характеристики.

Переходной функцией САР (или звена) называют функцию h(t), описывающую реакцию системы на единичное ступенчатое воздействие  при нулевых начальных условиях. График этой функции называют переходной характеристикой.

Импульсной переходной или весовой функцией (функцией веса) называют функцию w(t), описывающую реакцию САР (звена) на единичное импульсное воздействие  при нулевых начальных условиях. График этой функции называют импульсной переходной характеристикой.

Переходную и импульсную переходную функции называют временными функциями, а их графики – временными характеристиками.

Между ПФ в изображениях Лапласа, переходной функцией и весовой функцией существует взаимнооднозначное соответствие.

Из определения импульсной переходной функции следует, что в (2) будет  при , или в изображениях Лапласа:

           при  (см. табл. 2.1)

Подставив эти выражения в (2), получим, что

              ,

то есть, изображения Лапласа импульсной переходной функции и передаточной функции САР равны.

Это означает, что, если известна ПФ замкнутой САР , то импульсная переходная функция  может быть определена с помощью обратного преобразования Лапласа:

              .                        (3)

Для отыскания оригинала  по его изображению Лапласа  часто пользуются таблицами изображений (табл.2.1) и теоремой разложения. Если

              ,

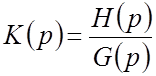и все  полюсов (нули полинома ) простые, причем нулевой полюс отсутствует, то оригинал может быть найден по формуле:

              ,

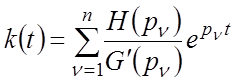где 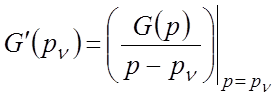 – характеристический полином без учета множителя , обусловленного наличием -го корня, вычисленный при .

Если же присутствует нулевой полюс (), то характеристический полином предварительно нужно представить в виде

             

(т.е., вынести нулевой полюс за скобки), и затем воспользоваться формулой: