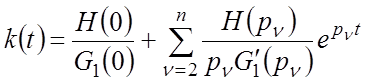Характеристики замкнутых САР и процессы в них, страница 2

                        .

Импульсная переходная функция является исчерпывающей динамической характеристикой САР в том смысле, что, зная ее, всегда можно определить реакцию САР на любое воздействие.

Из определения переходной функции следует, что в (2) будет  при , или в изображениях Лапласа:

           при 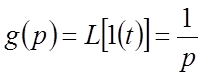 (см. табл. 2.1)

Подставив эти выражения в (2), получим, что

          .

Если для этого выражения применить обратное преобразование Лапласа, то в левой части, согласно (3), будем иметь импульсную переходную функцию, а в правой части – производную от переходной функции по времени (см. табл.2.2):

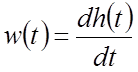              .                        (4)

Уравнение САР во временной области может быть получено путем применения к (2) обратного преобразования Лапласа и использования теоремы свертки (табл.2.2):

.

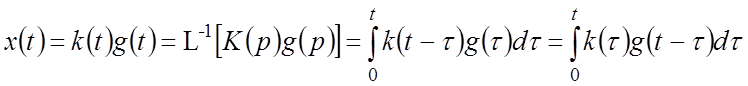Напомним, что функции ,  и  являются функциями-оригиналами, которые при отрицательном аргументе равны нулю.

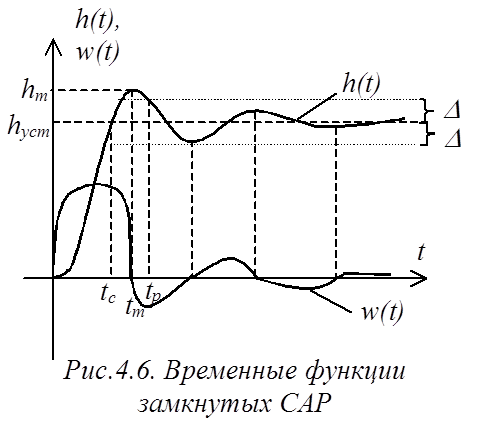Качественно временные характеристики замкнутых САР имеют вид, показанный на рис.4.6. При этом переходная функция h(t) замкнутой системы  имеет следующие показатели:

h_уст – установившееся значение переходной функции (регулируемой координаты);

h_m – максимальное значение;

D – величина, определяющая окрестность точки h_уст, внутри которой процесс можно считать установившимся (обычно в технических системах );

t_c – время первого согласования переходной функции с установившимся значением;

t_m – время достижения переходной функцией значения h_m;

t_p – время регулирования, по истечении которого переходный процесс войдет в зону  и больше из нее не выйдет.

Временные показатели t_c, t_m, t_p характеризуют быстродействие САР.

Колебательность САР характеризуется показателем перерегулирования, который обычно измеряется в процентах:

          .

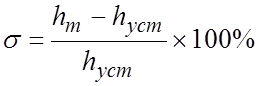Понятие установившегося и свободного процессов.

Частотная функция

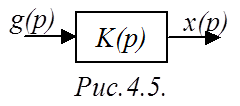Реакция САР (рис.4.5) на произвольное воздействие  может быть определена по выражению:

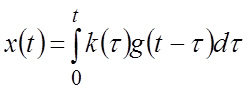          ,                                   (1)

где t – время наблюдения за реакцией САР.

Как известно из курса ТОЭ, при переходном процессе в нормально функционирующей системе все величины (координаты САР) состоят из установившихся (вынужденных) и свободных составляющих.

Таким образом для рассматриваемой САР, если устремить , выражение (1) будет описывать вынужденный процесс, который имеет место после затухания всех свободных составляющих

.

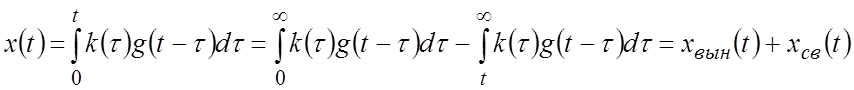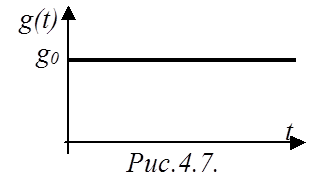Пример 1. Определить вынужденный процесс в САР рис.4.5 при скачкообразном воздействии (рис.4.7):

.

Вынужденный процесс:

,

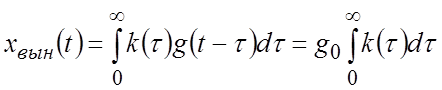поскольку . Второй множитель есть не что иное, как ПФ САР 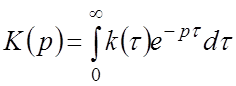 при , т.е. .

Из этого выражения видно, что вынужденный процесс от скачкообразного воздействия не зависит от времени и пропорциональный площади, ограниченной импульсной характеристикой САР:

          .

Таким образом, вынужденный процесс от постоянного (скачкообразного) воздействия равен произведению величины этого воздействия на ПФ  при .

Этот же результат можно получить, если учесть, что в рассматриваемом примере  (табл.2.1), и воспользоваться теоремой о конечном значении (табл.2.2), согласно которой

.

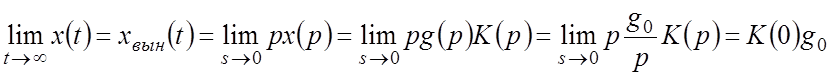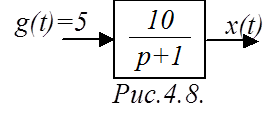Например, для САР рис.4.8 вынужденный процесс будет:

          .

Пример 2. Определить вынужденный процесс при гармоническом воздействии

          .

Вычислим

                    .

Вынужденный процесс:

.

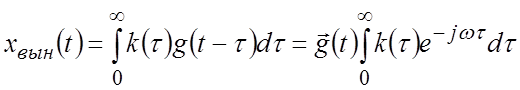Второй множитель есть ПФ САР 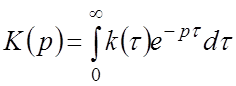 при .

Тогда

          .

Зависимость 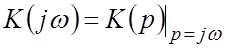 называется частотной передаточной функцией САР.

Таким образом, вынужденный процесс от гармонического воздействия является также гармоническим, и равен произведению частотной функции на входное воздействие.

Частотные характеристики и их физический смысл

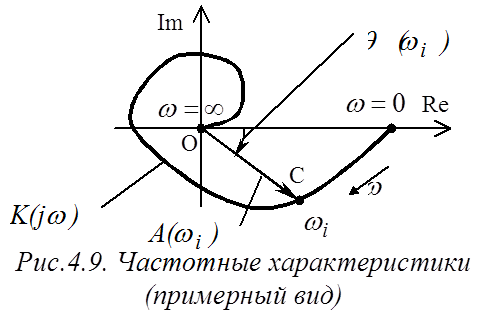
Частотную функцию САР изображают графически на комплексной плоскости при изменении частоты  гармонического сигнала от нуля (или от ) до  (рис.4.9). Такой график изменения положения годографа частотной функции при изменении частоты называется частотной характеристикой.

Частотную характеристику можно представить в следующем виде:

          ,

где  – амплитудно-частотная характеристика (АЧХ) САР, равная длине годографа частотной характеристики (рис.4.9);

       – фазо-частотная характеристика (ФЧХ) САР, равная угловому положению годографа частотной характеристики (рис.4.9).

Таким образом, АЧХ есть коэффициент передачи между амплитудой входного гармонического сигнала и амплитудой выходного сигнала. Другими словами, значение АЧХ при определенной частоте входного гармонического сигнала равно отношению амплитуды выходного сигнала к амплитуде входного сигнала.

ФЧХ характеризует сдвиг по фазе выходного гармонического сигнала относительно входного. Если , то выходной сигнал отстает по фазе от входного сигнала, в противном случае – опережает.

Таким образом, если САР работоспособна, то при входном воздействии  после окончания переходного процесса выходной сигнал будет иметь вид:

                    .

Пример. Построить частотную характеристику САР с ПФ

          ,

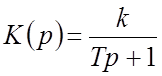где  и  – некоторые коэффициенты.

Решение. Записываем выражения для частотных характеристик:

;

;

.

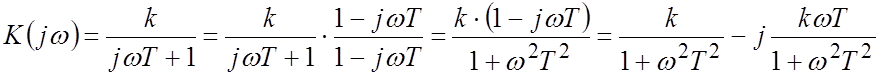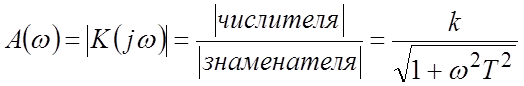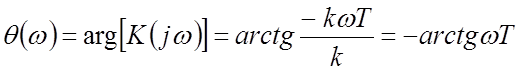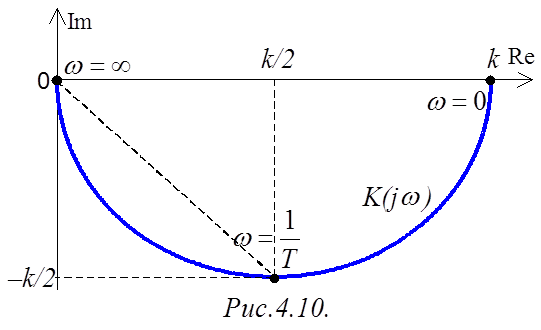
Строим  на комплексной плоскости при изменении  от 0 до  (рис.4.10) по характерным точкам:

0	k	k	0
1/T		0,707k
	0	0

Очевидно, что с ростом частоты  снижается, а  возрастает. В действительности частотная характеристика  будет иметь форму полукруга (рис.4.10). Графическое же изображение АЧХ и ФЧХ будет очень неудобным для восприятия, поэтому используют так называемые логарифмические частотные характеристики.

Логарифмической амплитудно-частотной характеристикой (ЛАЧХ) называется зависимость

          ,

которая строится в осях lg w, L (рис.4.11а).

Логарифмической фазо-частотной характеристикой (ЛФЧХ) является зависимость , которая строится в осях lg w, q (рис.4.11а).

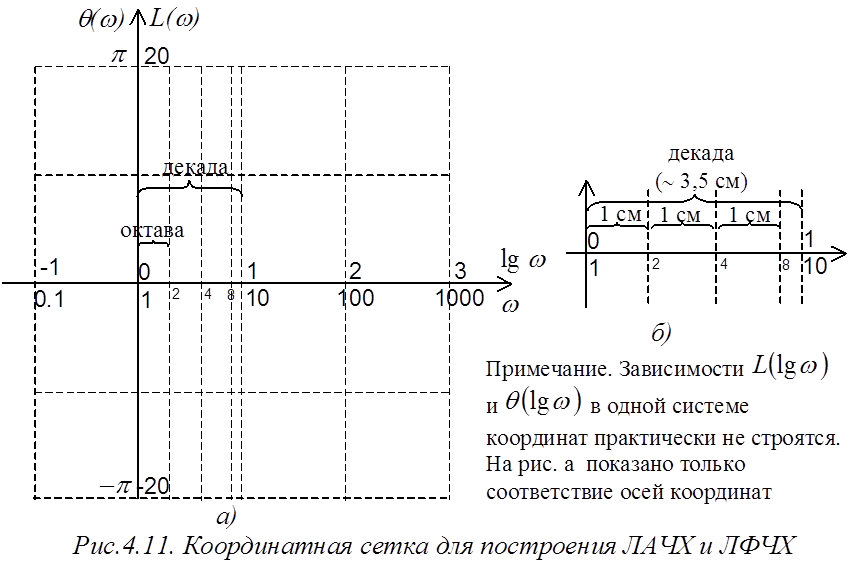
Отрезок на оси абсцисс, соответствующий увеличению частоты в 2 раза, называется октавой; соответствующий увеличению частоты в 10 раз – декадой.

При построении ЛАЧХ и ЛФЧХ вручную на бумаге в клетку можно воспользоваться приближенными соотношениями октавы и декады, приведенными на рис.4.11б.

Например, для рассмотренного выше примера при k=2, T=0,1 ЛАЧХ и ЛФЧХ имеют вид, представленный на рис.4.12.

 

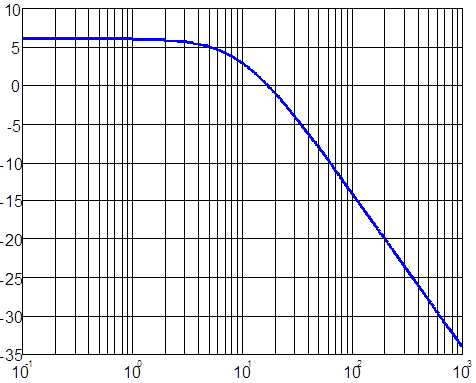
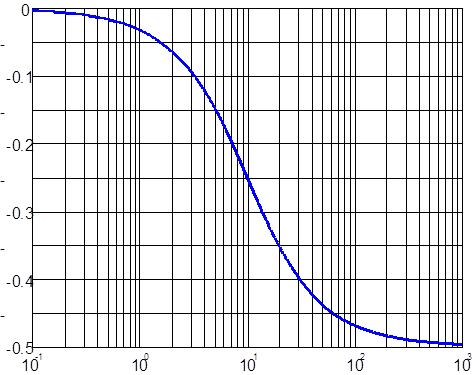
а)                                                          б)

Рис.4.12. ЛАЧХ (а) и ЛФЧХ (б) для САР из примера.