МОДЕЛИРОВАНИЕ НА МИКРОУРОВНЕ
Уравнение нагрева диска:
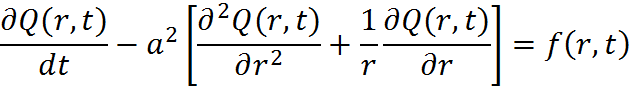
Входное воздействие, начальные и граничные условия:
![]()
Q(r,0)=Q0(r)=Ar2+B
![]()
![]()
Стандартизирующая функция:
![]()
![]()
Функция Грина:
G(r,ρ,t)= 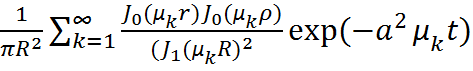
Континуальная передаточная функция:
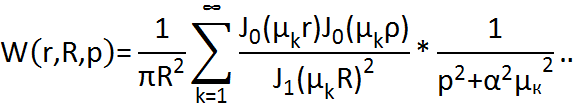
ИДЕНТИФИКАЦИЯ КРАЕВОЙ ЗАДАЧИ
Входное
воздействие ![]()

рисунок 1 - изображение диска рисунок 2 - граничное
в начальный момент времени условие на конце диска
Стандартизирующая функция с учетом принятых условий имеет вид:
ω(r,t)=(2r2+0,3)δ(t)+4.7·10-13δ`(10-r)·5cos(0.25t)+10
Значение коэффициента температуропроводности материала a=6,8·10-7 [м/с].
Соблюдение размерности:
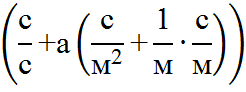
РАСЧЕТ ВЫХОДНОЙ РАСПРЕДЕЛЕННОЙ ВЕЛИЧИНЫ
Выражение для расчета выходной распределенной величины:
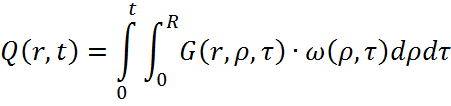
|
 ,
,
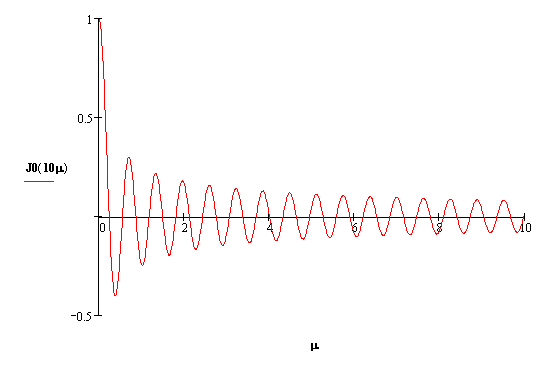
Рисунок 3 – График функции Бесселя
С учетом размеров диска R=10м и коэффициентов μk получим:
![]()

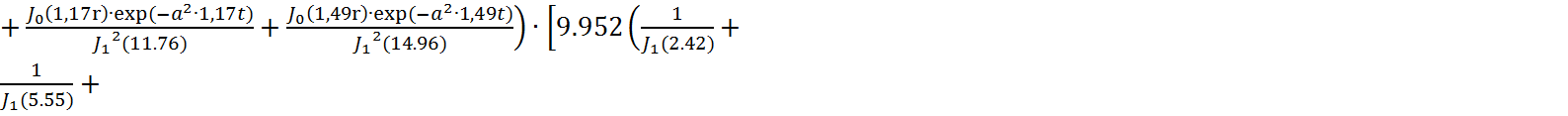
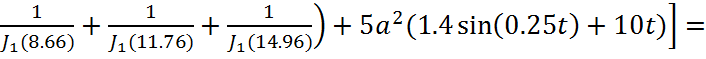

![]()
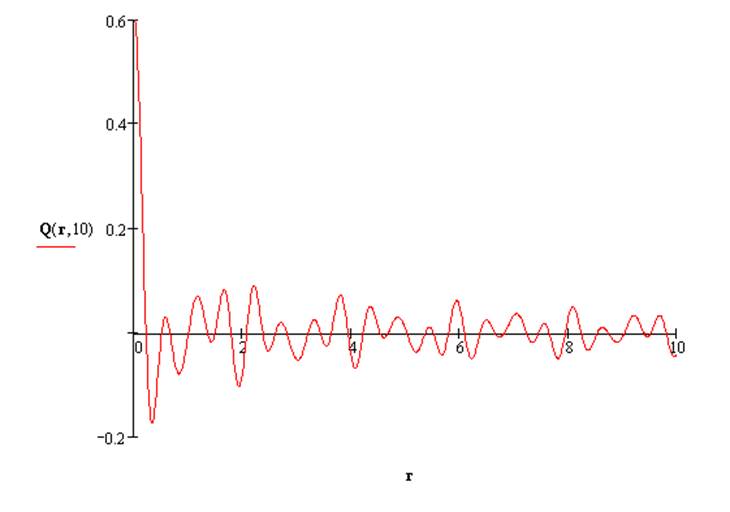
Рисунок 4 - График выходной величины Q(r,t) при R=10м и t=10 c
РАСЧЕТ ДИНАМИЧЕСКОЙ ХАРАКТЕРИСТИКИ
Производная по Лапласу от стандартизирующей функции:
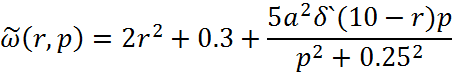
Т.к. на систему не действует входное воздействие, то:
![]()
Выражение для расчета интегральной передаточной функции:
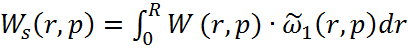
Рассчитанная интегральная передаточная функция:
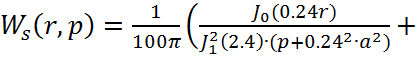
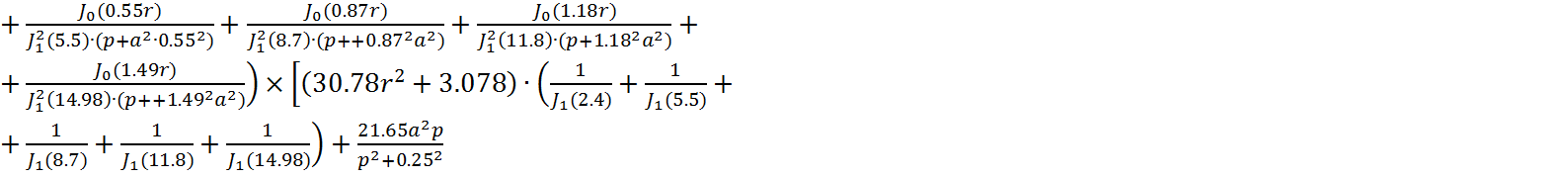
Интегральная функция в частотном виде
![]()
![]()
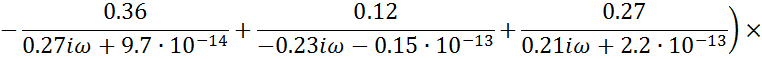
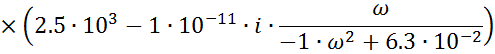
Логарифмическая амплитудно-частотная характеристика:
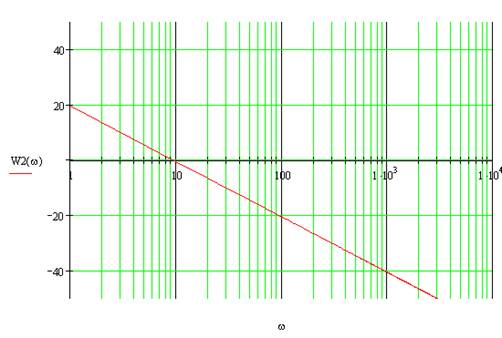
Аппроксимируем полученную ЛАЧХ стандартными типовыми наклонами получаем -20 дБ/дек.
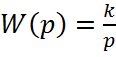 (1.35)
(1.35)
20logk=1, следовательно, k=10.
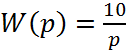 .
.
Моделирование колебания струны в среде Elcut:
МОДЕЛИРОВАНИЕ НА МАКРОУРОВНЕ
Принципиальная схема гидравлической системы
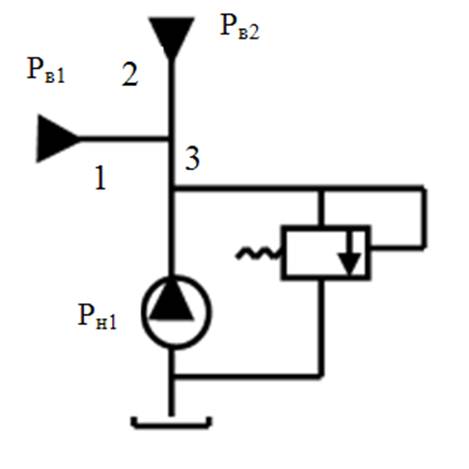
1,2,3 – магистрали потребителей; РВ1, РВ2 – давление потребителей; PH1 – насосы.
ИСХОДНЫЕ ДАННЫЕ
Параметры системы и жидкости
|
Основные параметры |
Обозначение |
Значение |
|
Плотность рабочей жидкости, кг/м3 |
ρ |
860 |
|
Вязкость, м2/с |
ν |
0.15×10-4 |
|
Модуль упругости системы, Па |
Eс |
1.7×108 |
|
Модуль упругости трубопровода, Па |
Eтр |
2.1×1011 |
|
Коэффициент потерь на трение при турбулентном потоке |
λт |
0.03 |
|
Толщина стенки трубопровода, м |
δтр |
2.2×10-3 |
Параметры трубопроводов
|
Параметр |
Обозначение |
Номер магистрали |
||
|
1 |
2 |
3 |
||
|
Диаметр трубопровода, м |
dтр |
20 |
20 |
20 |
|
Длина трубопровода, м |
l |
0,9 |
0,8 |
0,7 |
|
Коэффициент местных сопротивлений |
ζ |
2,9 |
2,8 |
2,7 |
|
Давление потребителей и насосов, МПа |
p |
0,1/- |
0,2/- |
0,25/0,5 |
ГРАФИЧЕСКИЕ И ТАБЛИЧНЫЕ ФОРМЫ МОДЕЛИ
Динамическая модели гидравлической системы
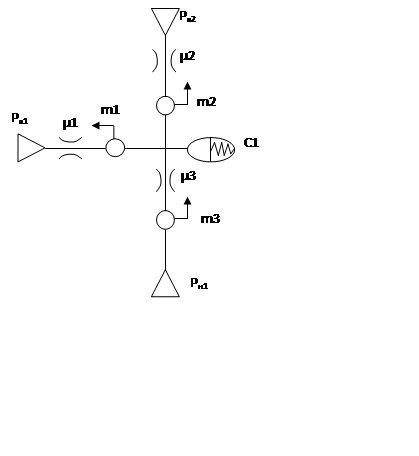 |
|
Узлы |
Ветви |
||||||
|
Диссипативные узлы |
Упругие |
Внешнее воздействие |
|||||
|
μ1 |
μ2 |
μ3 |
С1 |
Pв1 |
Pв2 |
Pн1 |
|
|
1 |
-1 |
0 |
0 |
1 |
-1 |
0 |
0 |
|
2 |
0 |
-1 |
0 |
1 |
0 |
-1 |
0 |
|
3 |
0 |
0 |
-1 |
-1 |
0 |
0 |
1 |
|
Ав |
Ау |
Ад |
|||||
ГИДРАВЛИЧЕСКОЙ СИСТЕМЫ
Ориентированный граф гидравлической системы
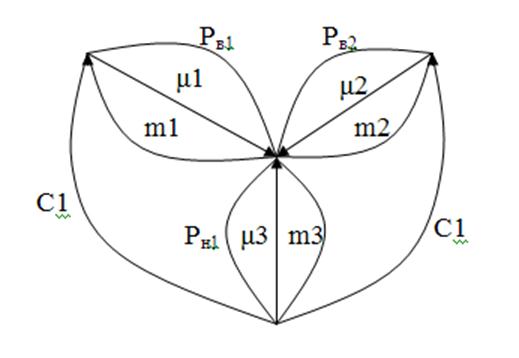
РАСЧЕТ СТАТИЧЕСКОГО РЕЖИМА РАБОТЫ ГИДРОСИСТЕМЫ
Система уравнений, математически описывающая функционирование гидравлической системы:
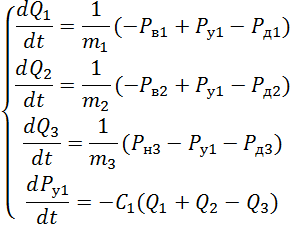
Полагая
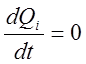 и
и 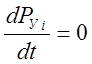 ,
получим статическую модель системы:
,
получим статическую модель системы:
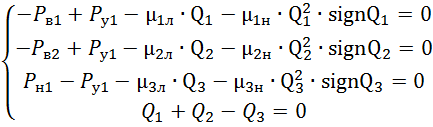
Матрица Якоби
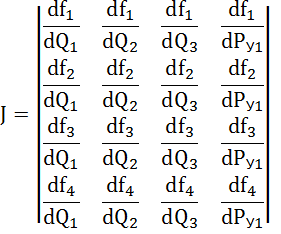
Алгоритм реализующий расчет статического анализа
 Результаты статического анализа
Результаты статического анализа
|
Фазовые координаты |
Pн1=0.25*106 Па |
Pн1=0.5*106 Па |
|
Q1, м3/c |
3,638*10-4 |
9,22*10-4 |
|
Q2, м3/c |
6,91*10-4 |
1,796*10-3 |
|
Q3, м3/c |
1,055*10-3 |
2,718*10-3 |
|
Ру, Па |
2,053*105 |
2,272*105 |
РАСЧЕТ ДИНАМИЧЕСКОГО РЕЖИМА РАБОТЫ ГИДРОСИСТЕМЫ
Система дифференциальных уравнений, составляющая динамическую гидросистему:
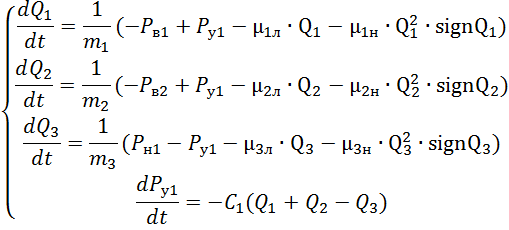
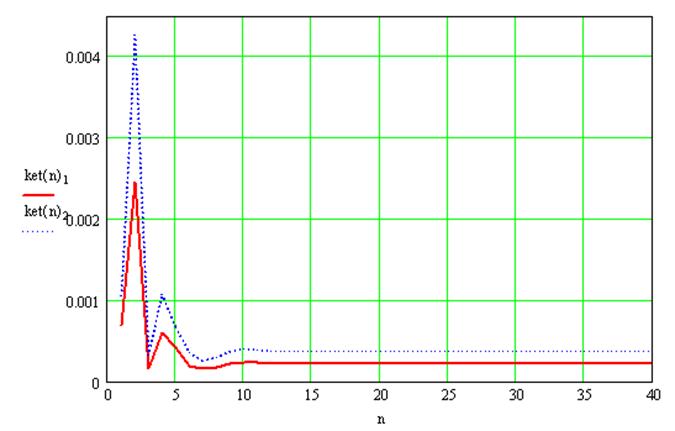
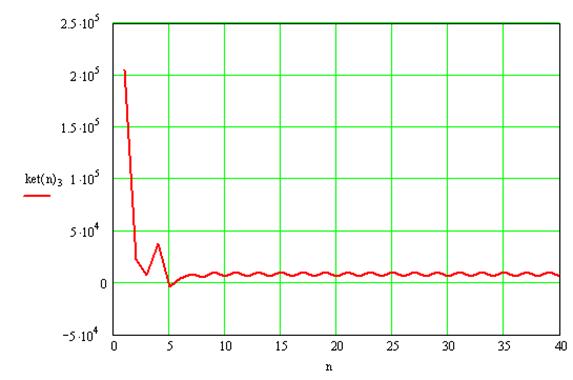
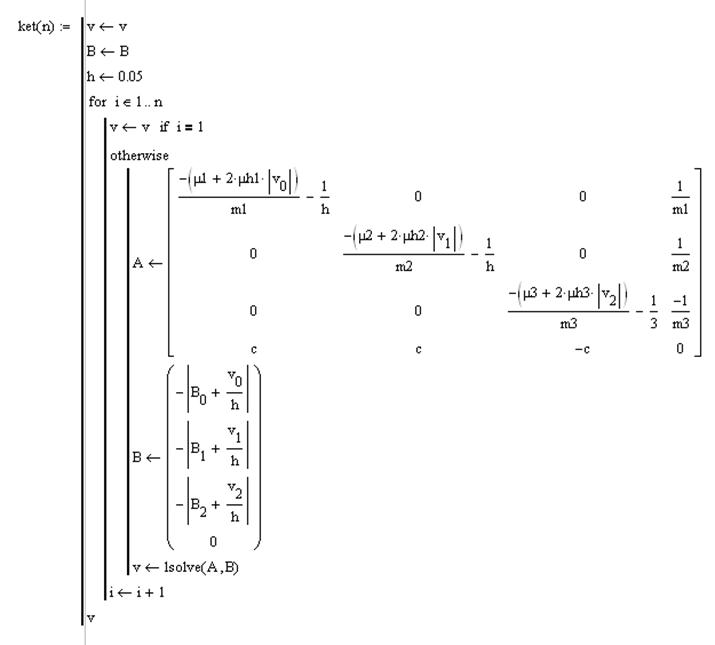
Переходный процесс гидросистемы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.