Аналитические методы анализа динамики математических моделей систем: метод возмущения, асимптотических разложений. Численные методы анализа динамики математических моделей. Погрешности численных методов анализа динамики математических моделей систем

16. Аналитические методы анализа динамики мат. моделей систем: м-д возмущений.

Рассмотрим динамику популяций 2-х видов, взаимодействующих м/у собой по типу «хищник-жертва». Построим мат.модель, предполагая, что жертва может найти достаточно пищи для пропитания, но при каждой встрече с хищником последний убивает жертву.

х(t)-кол-во жертв; y(t)-кол-во хищников, x_B-кол-во рожденных жертв, x_d-естественная смертность жертв,

(x_B-x_d)*x(t) – скорость пополнения популяции жертв

x(t)*y(t) – число случаев, когда хищник убивает жертву, зависит от вероятности их встречи.

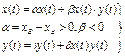уравнение Лотки-Вольтерра

где γ<0, δ>0, γ - естественная смертность, δ - вероятность встреч.

Для полной постановки задачи зададим рассматриваемый промежуток времени , тогда кол-во хищников и кол-во жертв в нач время x(t₀)=x₀, y(t₀)=y₀

Поскольку аналитическое представление реш-я задачи (1.1) и (1.2) затруднительно, то используют приближенный м-д, основанный на теории возмущ-я.

Первый шаг состоит в определении стационарных точек (x_S, y_S), к-рые также наз-ся точками равновесия. В данном случае стац сост-е будет определяться:

т.к

, то

разложив равные части в ряд Тейлора, получим:

x(α+βy)=βx_S(y-y_S)…

y(γ+δx)=δy_S(x-x_S)…

В окрестности данной точки мы можем разбить исх. ур-я лин-ми:

x=βx_S(y-y_S)

y=δy_S(x-x_S), используя аппарат высшей математики, получим:

На рис. показано семейство подобных эллипсов с центром в точке (x_S, y_S), причем стрелками указываются направ-я соответствующие возрастанию времени.

17. Аналитический метод анализа динамики мат. моделей сис-м: м-д асимптотических разложений.

Рассмотрим задачу нахожд-я реш-й ММ сис-ы, описываемые диф. ур-ем:

для больших t (t>>1)

  (1.1)

Известно, что интеграл сходится при t→ ∞ следовательно принимаем t=∞

(1.2)

Если ур-е (1.2) подставим в ур-е (1.1), то получим:

Получим второе приближение:

      (1.3)

это выраж-е (1.3) подставим в (1.1), получим:

1 интеграл преобразовывается интегрированием по частям, а второе – по формуле тригонометрии, оставшиеся интегралы входят в величину

3 приближение:

18. Численные м-ды анализа динамики мат. моделей

При реш-и численных м-дов также исп-ся преобраз-я Коши.

Пусть дано диф. ур-е:

                     (1.1)

с нач. усл-ями: ;

Найти x(t).

Обычные численные реш-я данной задачи получают, вычисляя знач-я производной при фиксированном значении t_k. Затем задают малые приращения h по независимой перем-ой t:

    (1.2)

Если д/нахожд-я след.точки x_k+1 требуется инф-ция о предыдущем шаге, то метод наз. одношаговым (метод Рунге-Кутта).

19. Погрешности численных методов анализа динамики мат моделей систем

Источники погрешностей:

1. может оказаться, что нач усл-я x(t₀) известны неточно и опред-ся в рез-те эксперимента или в рез-те реш-я какой-либо другой задачи. В данном случае вместо точного нач. усл-я приходится исп-ть его приближение. А вместо задачи Коши решать задачу ,     (1.1)

с изменяемыми нач усл-ями . Т.о., реш-е задачи (1.1) зависит от  и не совпадает с искомым реш-ем x(t).

 наз-ся неустранимой погрешностью реш-я .

2. погрешность округления обусловлена ограничениями представления чисел на ЭВМ и как следствие погрешность вычисляется правой части ур-я                         (1.2) и по формуле (1.3). Фактически найденные знач-я удовлетворяет не уравнению (1.3), а условию

 - наз-ся погрешностью округления на k-том шаге.

3. погрешность метода или сечения

              (1.4)

              (1.5)

                                          (1.6)

           (1.7)

Погреш-ть м-да связана с тем, что при аппроксимации ф-ции правой части ур-я (1.2) вместо бесконечных рядов часто исп-ся лишь несколько первых членов. Данная погрешность может быть определена как разность м/у истинным знач-ем реш-я  (1.1) и его приближенным знач-ем , полученное по ф-ле (1.3).

(1.4) разность м/у точным реш-ем  задачи (1.2) и приближенным фактически найденным знач-ем  наз-ся полной погреш-тью приближенного реш-я (1.5). (1.6) наз-ся вычислительной погреш-тью. Исходя из соотношений погреш-ти , (1.4), (1.5), (1.6) следует (1.7).

Полная погреш-ть приближенного м-да равна сумме неустранимой погреш-ти, погреш-ти м-да и вычислительной погреш-ти. Указанные источники погреш-ти явл-ся причиной наблюдаемости 2-х ошибок: 1. локальные ошибки; 2. глобальные ошибки.

20. Численные м-ды анализа динамики мат. моделей: одношаговые м-ды реш-я задачи Коши

Пусть требуется найти реш-я задачи         (1.1) на отрезке . Разобьем данный отрезок точками  эти точки наз. сеткой, а N узлами сетки.

Рассмотрим м-ды вида             (1.2), который послед-но дает приближ-е  к знач-ю точного реш-я  в каждом узле сетки  на основе известного приближ-я  в предыдущем узле .

В общем виде их можно записать:

Простейшим одношаговым м-дом явл-ся м-д Эйлера. Он основан на разложении реш-й x(t) в окрестности точки  в ряд Тейлора. Если предположить, что правая часть ур-я f=x(t) диф ур-ем (1.1) имеет непрерывные частные производные до порядка s, то искомые реш-я x(t), также имеют непрерывные производные до (s+1) порядка, при этом точное реш-е в узле  будет иметь вид:

             (1.3)

, k=0,1,…,N     (1.4)

Предположение, что h мало можно пренебречь в ур-е (1.3) членами содержащими h во II или более порядками, тогда явный м-д Эйлера может быть определен след образом (1.4). Т.о., можно получить приближенное знач-е зависимой перем-ой при малом смещении h от текущей точки. Следует отметить, что разлож-е x(t) в ряд Тейлора, аналогично (1.4) можно выполнить и в окрестности точки .

     (1.5)

,

М-ды, полученные по этой ф-ле, образуют семейство одношаговых м-дов. Простейшим из них явл-ся неявный м-д Эйлера, получаемый из ур-я (1.5).

Нем. математик Рунге предложил след. идею, основанную на вычислении приближенного реш-я  в узле  в виде лин-ой комбинации с постоянными коэф-тами:

       (1.6)

где ,

Числа , ,  выбираются так, чтобы разлож-е выраж-я (1.6) по степеням h совпало с разлож-ем (1.3) или (1.5) до максимально возможной степени при произвольной правой части и произвольном шаге h. Если ввести вспомогательную функцию , то разлож-е по степеням h должно начинаться с max возможной степени.

Величина φ(h) наз погрешностью м-да на данном шаге или локальной погреш-тью м-да.

Ф-ла (1.6) образует семейство м-дов Рунге-Кутта порядка s и для их реализации требуется s  вычислений функции f(t, x(t)), представляющих собой производные реш-я.

Если =0 при j≥i для всех i, то  вычисляется в явном виде. Если =0 при j>i и , то каждая  неявно определяется ур-ем: . В данном случае необходимо каким-либо способом вычислить , например, с помощью итерации по м-ду Ньютона.

Примером явного м-да Рунге-Кутта явл-ся м-д Хойна, к-рый в случае, если правая часть ур-я (1.1) не зависит от t переходит в квадратичную форму трапеции, при этом s=2, a₁₁=0, a₁₂=0, a₂₁=1, a₂₂=0, b₁=b₂=0,5, c₁=0, c₂=0.

, ,

Всем одношаговым м-дам присуще общие черты: 1. чтобы получить инф-цию о новом узле необх-мо иметь инф-цию об одном предыдущем; 2. в основе всех одношаговых м-дов лежит разлож-е функции правой части ур-я (1.1) в ряд Тейлора; 3. все одношаговые м-ды не требуют действительного вычисления производной, вычисляется лишь сама функция, знач-е к-рой могут потребоваться в неск-ких промежуточных точках.