1.2 Выбор и идентификация уравнения
Исходное уравнение, описывающее колебания мембраны, имеет следующий вид:
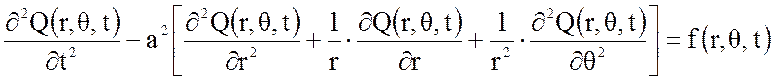 , (4)
, (4)
Зададим размерность выходного сигнала ![]() (первичная размерность)
– ортогональная деформация мембраны.
(первичная размерность)
– ортогональная деформация мембраны.
Тогда вторичная размерность (входной сигнал) будет равна:
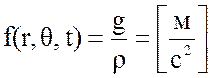 ,
(5)
,
(5)
где g – поверхностное усилие на мембрану, [Н/м2];
![]() – поверхностная погонная плотность мембраны,
[кг/м2].
– поверхностная погонная плотность мембраны,
[кг/м2].
То есть а с размерностью [м/с] в уравнении (4) является волновой скоростью мембраны. Волновая скорость определяется из выражения:
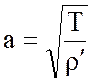 , (6)
, (6)
где Т – поверхностное натяжение мембраны, [Н/м2];
![]() - объемная плотность материала мембраны,
[кг/м3].
- объемная плотность материала мембраны,
[кг/м3].
Пусть входное воздействие на мембрану имеет вид:
![]() , (7)
, (7)
Знак «минус» в выражении (7) указывает на то, что давление на мембрану осуществляется сверху. Радиус мембраны R составляет 0,015 м, значит, входное воздействие можно представить в виде:
![]()
Начальные условия, определяющие положение мембраны и ее скорость в начальный момент времени:
![]() , (8)
, (8)
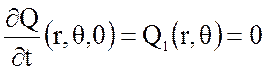 , (9)
, (9)
С учетом величины радиуса:
![]()
Граничные условия первого рода, определяющие перемещение мембраны на границе расчетной области:
![]() , (10)
, (10)
![]() , (11)
, (11)
Граничные условия равны нулю, так как мембрана жестко закреплена на границе и перемещение отсутствует.
Сформулированная выше задача принимается при условиях:
![]() ,
, ![]() ,
, ![]() ,
, ![]() (12)
(12)
Стандартизирующая функция для данной задачи запишется следующим образом:
![]() , (13)
, (13)
С учетом исходных данных:
![]()
1.3 Расчет выходной величины
Определим выходную величину, как тройной интеграл по радиусу, углу и времени от произведения функции Грина на стандартизирующую функцию. Функция Грина имеет вид:
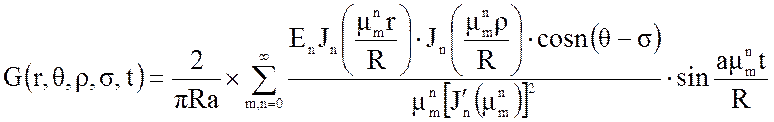 , (14)
, (14)
где ![]() - последовательные положительные корни
уравнения
- последовательные положительные корни
уравнения ![]() ;
;
![]()
![]() = ½ при n=0,
= ½ при n=0,
1 при n![]() 0.
0.
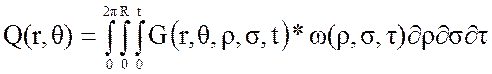 ,
(15)
,
(15)
При нахождении значения выходной величины ограничимся значениями функции Бесселя нулевого порядка, тогда получаем, что при решении интеграла по времени вся функция остается постоянной и находим только значения с синусом, зависящим от времени.
При решении интеграла по углу получаем аналогичную ситуацию с решением внутреннего интеграла по времени.
Функция Бесселя нулевого порядка
определяется последовательными положительными корнями уравнения ![]()
|
|
|
|
|
|
|
|
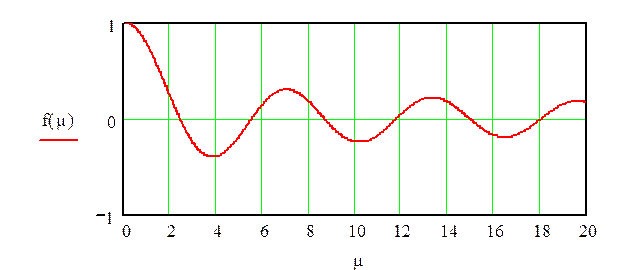
Приведем расчет последнего интеграла по радиусу:
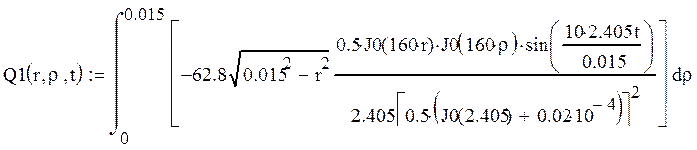
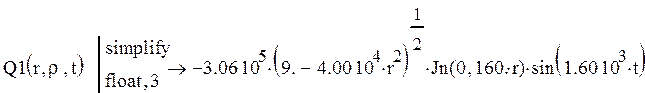
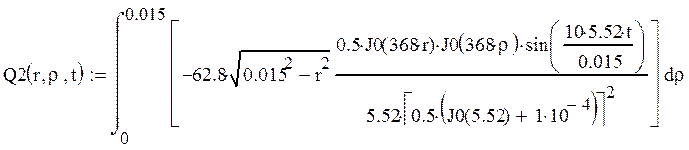
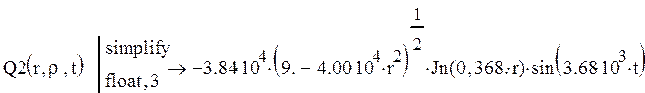
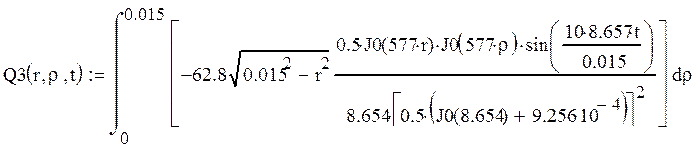
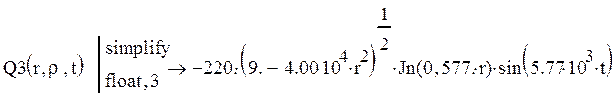
![]()
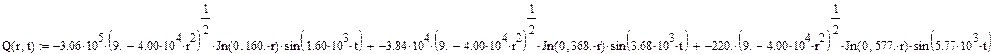
На рисунке 1 представлен график, показывающий зависимость выходной величины от радиуса и времени.
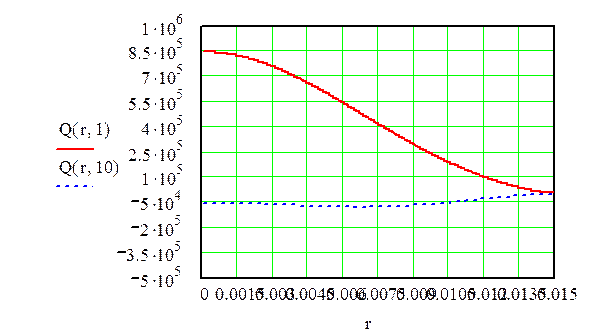
Рисунок 1 – График зависимости Q(r,t) от изменения радиуса
1.4 Расчет интегральной передаточной функции
Для определения динамической характеристики построим логарифмическую амплитудно-частотную характеристику. Для этого определим интегральную передаточную функцию, позволяющую для конкретной точки исследуемой области построить ЛАЧХ и по ней записать аппроксимированную передаточную функцию в сосредоточенных параметрах.
Континуальная передаточная функция имеет вид:
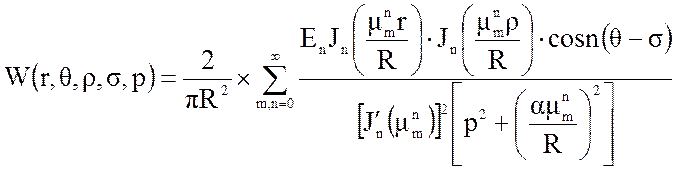 , (16)
, (16)
После допущений таких же, как и при нахождении выходной характеристики получаем:
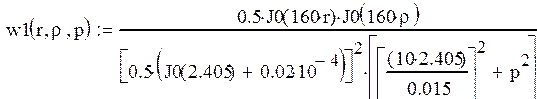
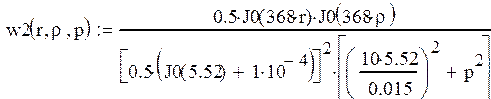
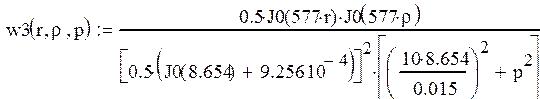
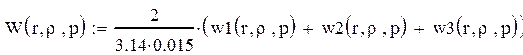
Найдем преобразование Лапласа от
стандартизирующей функции и выделим из нее входное воздействие, а оставшуюся
часть обозначим через ![]() .
.
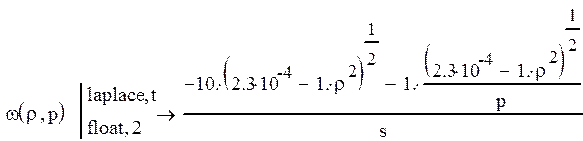
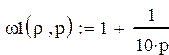
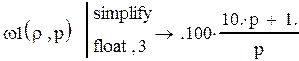
Найдем интеграл по пространственным
координатам упрощенной континуальной передаточной функции и ![]() :
:
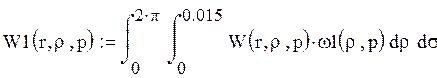
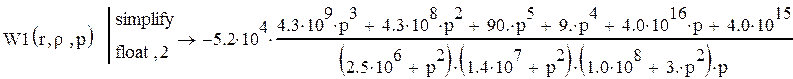
Тогда, выполнив переход к частотной передаточной функции, имеем:
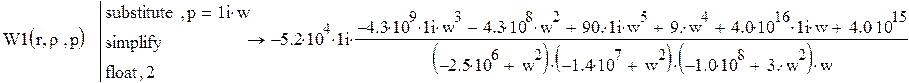
1.5 Построение логарифмических характеристик, синтез аппроксимированной передаточной функции
Логарифмическая характеристика представлена на рисунке 2.

![]()
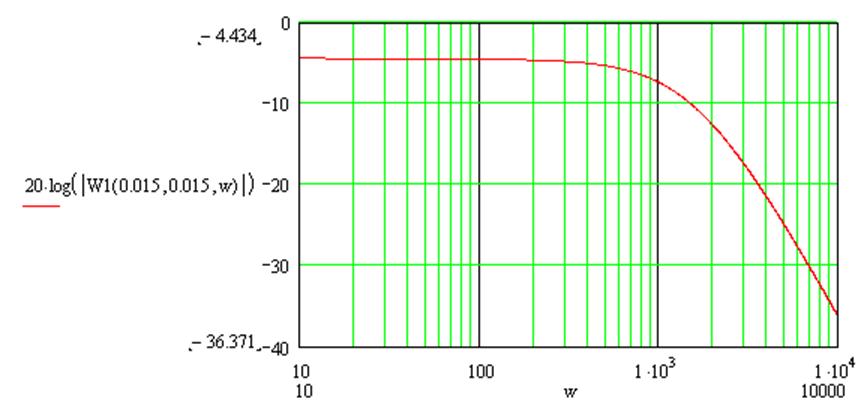
Рисунок 2 – ЛАЧХ
Данную ЛАЧХ, имеющую наклоны 0 , -40 Дб/декаду, можно аппроксимировать следующей передаточной функцией:
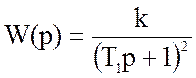 ,
(17)
,
(17)
Определим параметры передаточной функции:
- постоянные времени:
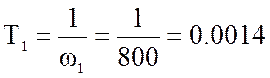 ;
;
- коэффициент усиления:
20log k = -5
k = 1.07
Тогда аппроксимированная передаточная функция:
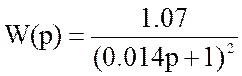
2 МОДЕЛИРОВАНИЕ НА МАКРОУРОВНЕ
2.1 Исходные данные
На рисунке 3 представлена схема гидросистемы, а в таблице 1 – основные параметры.
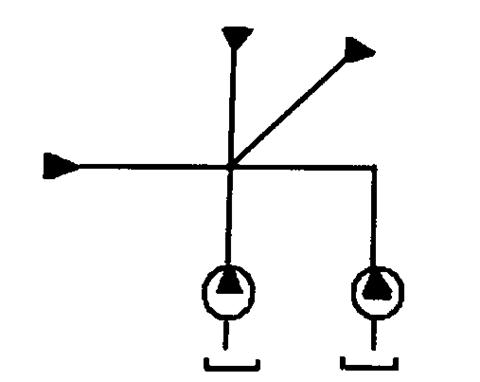
Рисунок 3 – Принципиальная схема гидросистемы
Таблица 1 – Параметры гидросистемы
|
Наименование параметра |
Обозн |
Номер магистрали |
|||||
|
1 |
2 |
3 |
4 |
5 |
|||
|
Диаметр, м |
dтр |
0,014 |
0,015 |
0,01 |
0,02 |
0,015 |
|
|
Длина, м |
l |
1,5 |
1 |
2 |
0,55 |
0,5 |
|
|
Толщина стенки трубопровода, м*10-4 |
δтр |
3*10-4 |
3*10-4 |
3*10-4 |
3*10-4 |
3*10-4 |
|
|
Коэффициент местных сопротивлений |
ζ |
5 |
3 |
5,5 |
2 |
1,5 |
|
|
Давление потребителя, Па*106 |
р |
0,1 |
0,15 |
0,19 |
|||
|
Рабочая жидкость |
Масло АУ ρ=860 кг/м3; υ=0,15*10-4 м2/с; Ес=1,7*108 Па |
||||||
|
Материал трубопровода |
Латунь Ес=9*1010 Па |
||||||
|
Коэф-т потерь на трение при турбулентном потоке |
λт=0,028 |
||||||
|
Номер схемы |
12 |
||||||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.